Реферат по дисциплине Дискретная математика на тему Функционально полные базисы булевых функций. Пять важнейших замкнутых класса T0, T1, S, L, M. Теорема Поста о функциональной полноте

• Название: Реферат по дисциплине Дискретная математика на тему Функционально полные базисы булевых функций. Пять важнейших замкнутых класса T0, T1, S, L, M. Теорема Поста о функциональной полноте
• Дата: 16.05.2022
• Размер: 150.12 Kb.
• Имя файла: lekcija_6_polnota_sistemy_bulevykh_funkcij.docx
• Тип: Реферат; #531890
• страница: 2 из 3

Поста.

T₀ ,

T₁ , S, L, Mназываются классами

Теорема 6.1 (критерий Поста). Система Fбулевых функций является полной тогда и только тогда, когда Fцеликом не содержится ни в одном из классов Поста.

В таблице приведены свойства, которыми обладают элементарные булевы функции (символ + отмечает свойство, которым обладает данная функция).
Свойства элементарных булевых функций.

Название	Обоз- начение	Не сохрани- мость кон- станты 0	Не сохрани- мость кон- станты 1	Не само- двойствен- ность	Не линей- ность	Не монотон- ность
Константа 0	0		+	+
Константа 1	1	+		+
Отрицание		+	+			+
Конъюнкция				+	+
Дизъюнкция				+	+
Импликация	→	+		+	+	+
Эквивалентность		+		+		+
Сумма по модулю 2			+	+		+
Штрих Шеффера	|	+	+	+	+	+
Стрелка Пирса		+	+	+	+	+

Используя теорему Поста и вышеприведенную таблицу можно строить базисы из элементарных функций по следующему правилу: выбрав любую элементарную булеву функцию и дополнив ее при необходимости другими функциями так, чтобы все они вместе удовлетворяли теореме о функциональной полноте. Через функции этого базиса можно выразить все

другие булевы функции.


1

1

2

2

2

2
Пример. Запишите функцию f x₁  x x₃  в базисе ,,.

1

2

3
Решение.

f x₁

 x

 x₃

  xx

 x₃

 xx

 x₃

 x₁ x₂ x₃

 x₂ x₃ 

1

1

2

2
 xx

 x₃

  xxx

x₂ x₃

 xxx

 x₂ x₃ .

3
Определение 2.6. Система Fбулевых функций называется замкнутой, если любая формула над Fпредставляет некоторую функцию из F .

Фундаментальным свойством каждого класса Поста является его

замкнутость (в смысле определения 2.6).


1

2
Чтобы исследовать полноту конкретной системы F f, f,..., f

n

булевых функций, используют критериальную таблицу:

	T0	T1	S	L	M
f1	+/–	+/–	+/–	+/–	+/–
f2	+/–	+/–	+/–	+/–	+/–
…	+/–	+/–	+/–	+/–	+/–
fn	+/–	+/–	+/–	+/–	+/–

Строки таблицы соответствуют функциям исследуемой системы, а

столбцы – классам Поста. Знак + означает, что функция не принадлежит соответствующему классу Поста.

Пусть, например, F ,,0. На основании таблицы свойств

элементарных булевых функций заполненная критериальная таблица имеет вид:

	T0	T1	S	L	M
	+	–	+	–	+
	–	–	+	+	–
0	–	+	+	–	–

Как видно из таблицы, система Fцеликом не содержится ни в одном из классов Поста (ни в одном столбце нет всех знаков «–»). Согласно теореме

1. 
   система функций является полной.
   

Исследуем на полноту систему, которая содержит булевы функции, не являющиеся элементарными.

Пусть, например, F f, f, где f xx, f x x.

1 2 1 1 2 2 1 2

Проверим, какими свойствами обладают данные функции:

1. 
   Сохранимость константы 0.
   

1
f00  0  0  0 1  0, т.е. fсохраняет константу 0;

1

2
f00  0  0 11 1, т.е.

f₂ не сохраняет константу 0.

2. 
   Сохранимость константы 1.
   

1
f11 1 1 1 0  0, т.е. fне сохраняет константу 1;

1


2
f11  1  1  0  0 1, т.е. fсохраняет константу 1.

2

3. 
   Самодвойственность.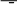
   

fx, x  xx x x fx, x

, т.е.

fне самодвойственная.

1 1 2

1 2 1

2 1 1 2 1

1

2

2
fx , x

  x

 x₂

 x₁

 x₂

 x₁

 x₂

 x₁ x₂ ;

fx , x

  x

 x₂

 x₁

 x₂ и

1

1

2

2

2

1

1

2
fx, x 

fx, x

, т.е.

f₂ не самодвойственная.

4. 
   
   1
   
   2
   
   2
   Линейность.
   

f₁ и f₂ не являются линейными. Объяснение этому будет дано далее .

5. 
   Монотонность.
   

Составим таблицу истинности для функции
f₁  x₁