не прерывные дроби. Не прерывные дроби
 Скачать 323.76 Kb.
|
|
Государственное бюджетное образовательное учреждение среднего профессионального образования Луганской Народной Республики «Луганский колледж информационных технологий и предпринимательства» Реферат Тема: «Не прерывные дроби» Выполнил обучающийся Группы 105 по профессии: «Мастер по обработки цифровой информации» Булко А.О. Луганск, 2022 Содержание Введение История цепных дробей Разложение в непрерывную дробь Приближение вещественных чисел к рациональным Приложения цепных дробей Свойства золотого сечения Введение Цепная дробь (или непрерывная дробь) — это математическое выражение вида 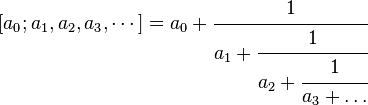 где a0 есть целое число и все остальные an натуральные числа (положительные целые). Любое вещественное число можно представить в виде цепной дроби (конечной или бесконечной). Число представляется конечной цепной дробью тогда и только тогда, когда оно рационально. Число представляется периодической цепной дробью тогда и только тогда, когда оно является квадратичной иррациональностью. 1. История цепных дробей Цепные дроби были введены в 1572 году итальянским математиком Бомбелли. Современное обозначение непрерывных дробей встречается у итальянского математика Катальди в 1613 году. Величайший математик XVIII века Леонардо Эйлер первый изложил теорию цепных дробей, поставил вопрос об их использовании для решения дифференциальных уравнений, применил их к разложению функций, представлению бесконечных произведений, дал важное их обобщение. Работы Эйлера по теории цепных дробей были продолжены М. Софроновым (1729-1760), академиком В.М. Висковатым (1779-1819), Д. Бернулли (1700-1782) и др. Многие важные результаты этой теории принадлежат французскому математику Лагранжу, который нашел метод приближенного решения с помощью цепных дробей дифференциальных уравнений. Алгоритм Евклида дает возможность найти представление (или разложение) любого рационального числа в виде цепной дроби. В качестве элементов цепной дроби получаются неполные частные последовательных делений в системе равенств, поэтому элементы цепной дроби называются также неполными частными. Кроме того, равенства системы показывают, что процесс разложения в цепную дробь состоит в последовательном выделении целой части и перевертывании дробной части. 2. Разложение в непрерывную дробь Последняя точка зрения является более общей по сравнению с первой, так как она применима к разложению в непрерывную дробь не только рационального, но и любого действительного числа. Разложение рационального числа имеет, очевидно, конечное число элементов, так как алгоритм Евклида последовательного деления a на b является конечным. Понятно, что каждая цепная дробь представляет определенное рациональное число, то есть равна определенному рациональному числу. Но возникает вопрос, не имеются ли различные представления одного и того же рационального числа цепной дробью? Оказывается, что не имеются, если потребовать, чтобы было. Непрерывные дроби - последовательность, каждый член которой является обычной дробью, порождает непрерывную (или цепную) дробь, если ее второй член прибавить к первому, а каждую дробь, начиная с третьей, прибавить к знаменателю предыдущей дроби. Любое вещественное число 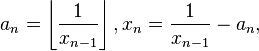 может быть представлено (конечной или бесконечной, периодической или непериодической) цепной дробью      где  обозначает целую часть числа .Для рационального числа это разложение оборвётся по достижении нулевого  для некоторого n. В этом случае представляется конечной цепной дробью  .Для иррационального все величины будут ненулевыми и процесс разложения можно продолжать бесконечно. В этом случае представляется бесконечной цепной дробью .Для рациональных чисел может быть использован алгоритм Евклида для быстрого получения разложения в цепную дробь. 3. Приближение вещественных чисел к рациональным Цепные дроби позволяют эффективно находить хорошие рациональные приближения вещественных чисел. А именно, если вещественное число разложить в цепную дробь, то её подходящие дроби будут удовлетворять неравенству Отсюда, в частности, следует: подходящая дробь  является наилучшим приближением для среди всех дробей, знаменатель которых не превосходит  ;мера иррациональности любого иррационального числа не меньше 2. 4. Приложения цепных дробей Теория календаря При разработке солнечного календаря необходимо найти рациональное приближение для числа дней в году, которое равно 365,2421988… Подсчитаем подходящие дроби для дробной части этого числа:  Первая дробь означает, что раз в 4 года надо добавлять лишний день; этот принцип лёг в основу юлианского календаря. При этом ошибка в 1 день накапливается за 128 лет. Второе значение (7/29) никогда не использовалось. Третья дробь (8/33), то есть 8 високосных лет за период в 33 года, была предложена Омаром Хайямом в XI веке и положила начало персидскому календарю, в котором ошибка в день накапливается за 4500 лет (в григорианском — за 3280 лет). Очень точный вариант с четвёртой дробью (31/128, ошибка в сутки накапливается только за 100000 лет) пропагандировал немецкий астроном Иоганн фон Медлер (1864), однако большого интереса он не вызвал. Другие приложения Доказательство иррациональности чисел. Например, с помощью цепных дробей была доказана иррациональность значения дзета-функции Римана  Решение в целых числах уравнения Пелля  и других уравнений диофантова анализа Определение заведомо трансцендентного числа (см. теорема Лиувилля) Алгоритмы факторизации SQUFOF и CFRAC Характеристика ортогональных многочленов Характеристика устойчивых многочленов 5. Свойства золотого сечения Интересный результат, который следует из того, что выражение непрерывной дроби для φ не использует целых чисел, больших 1, состоит в том, что φ является одним из самых «трудных» действительных чисел для приближения с помощью рациональных чисел. Теорема Гурвица утверждает, что любое действительное число k может быть приближено дробью m/n так, что Хотя практически все действительные числа k имеют бесконечно много приближений m/n, которые находятся на значительно меньшем расстоянии от k, чем эта верхняя граница, приближения для φ (то есть числа 5/3, 8/5, 13/8, 21/13 и т. д.) в пределе достигают этой границы, удерживая расстояние на почти точно  от φ, тем самым никогда не создавая столь хорошие приближения как, к примеру, 355/113 для π. Может быть показано, что любое действительное число вида (a + bφ)/(c + dφ), a,b, c и d являются целыми числами, причёмad − bc = ±1, обладают тем же свойством, как и золотое сечение φ; а также, что все остальные действительные числа могут быть приближены намного лучше.  дробь математический число уравнение |