Практика (Стась) 01.04. Решение дифференциальных уравнений операционным методом
 Скачать 81.17 Kb.
|
|
Решение дифференциальных уравнений операционным методом Постановка задачи Рассмотрим задачу, наиболее часто встречающуюся в теории дифференциальных уравнений, — задачу Коши для линейных дифференциальных уравнений и систем. 1. Пусть заданы: а) линейное обыкновенное дифференциальное уравнение с постоянными коэффициентами: где  — порядок дифференциального уравнения;  — заданные коэффициенты;  — заданная функция;б) начальные условия: 
Требуется найти решение  дифференциального уравнения, которое удовлетворяет начальным условиям (решить задачу Коши (5.24),(5.25)).Замечание 5.6. Переменная  в задачах анализа динамических систем имеет смысл времени. Поэтому будем использовать следующие обозначения производных:2. Пусть заданы: а) система линейных обыкновенных дифференциальных уравнений первого порядка с постоянными коэффициентами, записанная в нормальной форме:  (5.26)
где  — вектор неизвестных; матрица коэффициентов;  — заданная вектор-функция;б) начальные условия (где  — вектор начальных значений): (5.27)
Требуется найти решение  системы, которое удовлетворяет начальным условиям (решение задачи Коши (5.26),(5.27)).Во многих учебниках изложены классические аналитические и численные методы решения задачи Коши. Здесь будем предполагать, что заданная функция и искомая функция принадлежат классу оригиналов. Для решения задач (5.24),(5.25) и (5.26),(5.27) можно применить аппарат операционного исчисления метода решения задач, суть которого состоит в следующем.Поставленная в классе оригиналов задача переводится с помощью преобразования Лапласа в задачу для изображений. Эта задача решается, и определяете изображение искомой функции. Затем применяется обратное преобразование Лапласа и находится оригинал — решение поставленной задачи. Алгоритм решения задачи Коши операционным методом 1. Применить преобразование Лапласа: от известных и неизвестных функций перейти к их изображениям, записать уравнение (систему) в изображениях, соответствующее решаемой задаче Коши. 2. Решить полученное уравнение (систему): найти изображение искомого решения. 3. Применить обратное преобразование Лапласа: найти оригинал для полученного в п.2 изображения. Замечания 5.7 1. Преимущество операционного метода заключается в том, что при его применении функции из пространства оригиналов и производимые над ними операции заменяются функциями и операциями в пространстве изображений, которые оказываются более простыми. Так, вместо дифференциальных уравнений решаются алгебраические уравнения. 2. Начальные условия при записи уравнений в изображениях учитываются автоматически, и нет необходимости решать систему для нахождения произвольных постоянных, как это делается при применении классического метода. 3. Операционное исчисление позволяет найти не только частное, но и общее решение уравнения (5.24). Для этого достаточно положить  . При нахождении общего решения системы (5.26) следует принять  .4. Операционное исчисление можно применять для широкого класса кусочно-непрерывных функций и функций, заданных графически; для решения уравнений с переменными коэффициентами, уравнений в частных производных, интегральных и интегро-дифференциальных уравнений; для вычисления несобственных интегралов и суммирования рядов.5. При решении уравнения (системы) для изображений не следует приводить дроби к общему знаменателю, так как следующий этап — нахождение оригинала — связан с представлением дробей в виде суммы Как решить дифференциальное уравнение методом операционного исчисления? На данном уроке будет подробно разобрана типовая и широко распространенная задача комплексного анализа – нахождение частного решения ДУ 2-го порядка с постоянными коэффициентами методом операционного исчисления. Основная суть операционного исчисления состоит в следующем: функция действительной переменной  с помощью преобразования Лапласа отображается в функцию комплексной переменной  :  Терминология и обозначения:функция называется оригиналом; функция называется изображением;заглавной буквой  обозначается преобразование Лапласа.Действительную функцию (оригинал) по определённым правилам нужно превратить в комплексную функцию (изображение). Стрелочка  обозначает именно это превращение. А сами «определенные правила» и являются преобразованием Лапласа, которое рассмотрим лишь формально, чего для решения задач будет вполне достаточно. Осуществимо и обратное преобразование Лапласа, когда изображение превращается в оригинал:  В ряде задач высшей математики бывает очень выгодно перейти от оригиналов к изображениям , поскольку в этом случае решение задания значительно упрощается. Найти частное решение неоднородного уравнения второго порядка с постоянными коэффициентами  при заданных начальных условиях  .Примечание: иногда дифференциальное уравнение может быть и однородным:  , для него в вышеизложенной формулировке также применим метод операционного исчисления. Однако в практических примерах однородное ДУ 2-го порядка встречается крайне редко, и далее речь пойдёт о неоднородных уравнениях.Как известно, неоднородное дифференциальное уравнение 2-го порядка можно решить методом подбора частного решения по виду правой части либо методом вариации произвольных постоянных. И сейчас будет разобран третий способ – решение ДУ с помощью операционного исчисления. Ещё раз подчеркиваю то обстоятельство, что речь идёт о нахождении частного решения, кроме того, начальные условия строго имеют вид («иксы» равны нулям).К слову, об «иксах». Уравнение можно переписать в следующем виде: , где «икс» – независимая переменная, а «игрек» – функция. В рассматриваемой задаче чаще всего используются другие буквы:  То есть роль независимой переменной играет переменная «тэ» (вместо «икса»), а роль функции играет переменная «икс» (вместо «игрека») Понимаю, неудобно конечно, но лучше придерживаться обозначений, которые встречаются в большинстве задачников и методичек. Итак, наша задача с другими буквами записывается следующим образом: Найти частное решение неоднородного уравнения второго порядка с постоянными коэффициентами  при заданных начальных условиях  .Смысл задания нисколько не изменился, изменились только буквы. Как решить данную задачу методом операционного исчисления? Прежде всего, потребуется таблица оригиналов и изображений. Это ключевой инструмент решения, и без неё не обойтись. Поэтому, по возможности, постарайтесь распечатать указанный справочный материал. Сразу же поясню, что обозначает буква «пэ»: комплексную переменную (вместо привычного «зет»). Хотя для решения задач этот факт не имеет особого значения, «пэ» так «пэ». С помощью таблицы оригиналы  и  необходимо превратить в некоторые изображения. Далее следует ряд типовых действий, и используется обратное преобразование Лапласа (тоже есть в таблице). Таким образом, будет найдено искомое частное решение.Все задачи, что приятно, решаются по достаточно жесткому алгоритму. Пример 1 С помощью операционного исчисления найти частное решение дифференциального уравнения при заданных начальных условиях.  ,  ,  Решение: На первом шаге перейдем от оригиналов к соответствующим изображениям. Используем левую сторону таблицы оригиналов и изображений. Сначала разбираемся с левой частью исходного уравнения. Для преобразования Лапласа справедливы правила линейности, поэтому все константы игнорируем и по отдельности работаем с функцией  и её производными.По табличной формуле №1 превращаем функцию:  По формуле №2  , учитывая начальное условие  , превращаем производную:  По формуле №3  , учитывая начальные условия  , превращаем вторую производную: Не путаемся в знаках! Признаюсь, правильнее говорить не «формулы», а «преобразования», но для простоты время от времени буду называть начинку таблицы формулами. Теперь разбираемся с правой частью, в которой находится многочлен  . В силу того же правила линейности преобразования Лапласа, с каждым слагаемым работаем отдельно. Смотрим на первое слагаемое:  – это независимая переменная «тэ», умноженная на константу. Константу игнорируем и, используя пункт №4 таблицы, выполняем преобразование: Смотрим на второе слагаемое: –5. Когда константа находится одна-одинёшенька, то пропускать её уже нельзя. С одиночной константой поступают так: для наглядности её можно представить в виде произведения:  , а к единице применить преобразование: Таким образом, для всех элементов (оригиналов) дифференциального уравнения 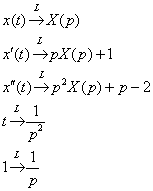с помощью таблицы найдены соответствующие изображения: Подставим найденные изображения в исходное уравнение : Дальнейшая задача состоит в том, чтобы выразить операторное решение  через всё остальное, а именно – через одну дробь. При этом целесообразно придерживаться следующего порядка действий: Для начала раскрываем скобки в левой части:  Приводим подобные слагаемые в левой части (если они есть). В данном случае складываем числа –2 и –3. Чайникам настоятельно рекомендую не пропускать данный этап:  Слева оставляем слагаемые, в которых присутствует , остальные слагаемые переносим направо со сменой знака: В левой части выносим за скобки операторное решение , в правой части приводим выражение к общему знаменателю: Многочлен слева следует разложить на множители (если это возможно). Решаем квадратное уравнение:  Таким образом:  Сбрасываем  в знаменатель правой части: Цель достигнута – операторное решение выражено через одну дробь.Действие второе. Используя метод неопределенных коэффициентов, операторное решение уравнения следует разложить в сумму элементарных дробей: 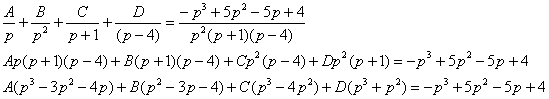 Приравняем коэффициенты при соответствующих степенях и решим систему:  Если возникли затруднения с методом неопределенных коэффициентов, пожалуйста, наверстайте упущенное в статьях Интегрирование дробно-рациональной функции и Как решить систему уравнений? Это очень важно, поскольку разложение на дроби, по существу, самая важная часть задачи. Итак, коэффициенты найдены:  , и операторное решение предстаёт перед нами в разобранном виде: Обратите внимание, что константы записаны не в числителях дробей. Такая форма записи выгоднее, чем  . А выгоднее, потому что финальное действие пройдёт без путаницы и ошибок:Заключительный этап задачи состоит в том, чтобы с помощью обратного преобразования Лапласа перейти от изображений к соответствующим оригиналам. Используем правый столбец таблицы оригиналов и изображений. Перейдем от изображений к соответствующим оригиналам:  Возможно, не всем понятно преобразование  . Здесь использована формула пункта №5 таблицы:  . Если подробнее:  . Собственно, для похожих случаев формулу можно модифицировать:  . Да и все табличные формулы пункта №5 очень легко переписать аналогичным образом.После обратного перехода искомое частное решение ДУ получается: Было: Стало:  Ответ: частное решение:  При наличии времени всегда желательно выполнять проверку. Проверка выполняется по стандартной схеме, Неоднородные дифференциальные уравнения 2-го порядка. Повторим: Проверим выполнение начального условия : – выполнено.Найдём первую производную:  Проверим выполнение второго начального условия : – выполнено.Найдём вторую производную:  Подставим  ,  и  в левую часть исходного уравнения : .Получена правая часть исходного уравнения. Вывод: задание выполнено правильно. Небольшой пример для самостоятельного решения: Пример 1 С помощью операционного исчисления найти частное решение дифференциального уравнения при заданных начальных условиях.  Пример 2 Найти частное решение дифференциального уравнения методом операционного исчисления.  ,  ,  |