1 Происхождение аликвотных дробей. 1 Происхождение аликвотных дробей в древнем Египте настоящими
 Скачать 21.56 Kb.
|
|
1 Происхождение аликвотных дробей В Древнем Египте «настоящими» математики считали только аликвотные дроби. Поэтому каждую дробь стремились представить в виде суммы аликвотных дробей, причём с разными знаменателями. Таким образом, первые дроби, с которыми нас знакомит история, это дроби вида  так называемые единичные дроби или аликвотные. То есть аликвотными дробями называются дроби с числителем 1.И даже сами аликвотные дроби они часто стремились представить в виде суммы меньших аликвотных дробей. Такие дроби использовались вместе с другими формами записи египетских дробей для того, чтобы поделить «хекат», основную меру объёма в Древнем Египте, т.е. аликвотные дроби нужны были египтянам в практических целях. Египтяне широко использовали дроби. Египетская дробь представляла собой сумму нескольких единичных (или аликвотных) дробей вида 1/n. Алгоритм разложения аликвотных дробей:1: числитель и знаменатель дроби надо умножить на сумму двух взаимно простых делителей знаменателя. 2: полученную дробь заменяем суммой двух дробей, знаменатели которых равны знаменателю полученной дроби, а числители – слагаемые вышеупомянутой суммы. 3: если знаменатель – простое число, то умножаем числитель и знаменатель на число, превышающее знаменатель на единицу: 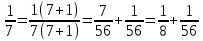 Вот формула алгоритма: 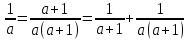 Итак разложим простую дробь на аликвотные: 1: 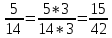 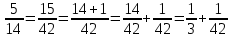 2: 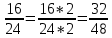 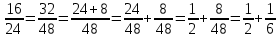 Гипотезы о причинах возникновения шестидесятеричной системы счисления. Однако именно в Древнем Междуречье возникла шестидесятеричная система счисления. Загадка её возникновения неоднократно привлекала умы математиков в течение последних двух тысяч лет. Создано несколько гипотез, каждая из которых освещала одну из сторон проблемы. Поэтому каждая из этих гипотез получила свою порцию критики, но это не значит, что они были неверными и не имели жемчужного зерна. Кратко об этих гипотезах: Теон Александрийский (конец 4 и начало 5 века н.э.) Теон полагает, что число 60 было выбрано вавилонянами за основание системы счисления в силу своих арифметических свойств: оно имеет наибольшее число различных делителей среди сравнительно небольших чисел. Гипотеза Тюро-Данжена (1932) Тюро-Данжен предположил, что в древнейшее время вавилонская нумерация имела смешанный десятично-шестеричный характер; единицей второго разряда служила десятка; единица же третьего разряда образовалась из шести единиц второго разряда, так что роль нашей "сотни" играло число 60. Тюро-Данжен считает, что причина этого в том, что число 6, делящееся на 2 и 3, оказалось более удобным по своей арифметической структуре. Гипотеза Нейгебауера (1927) Гипотеза О. Нейгебауэра заключается в том, что после аккадского завоевания шумерского государства там долгое время одновременно существовали две денежно-весовые единицы: шекель (сикль) и мина, причём было установлено их соотношение 1 мина = 60 шекелей. Позднее это деление стало привычным и породило соответствующую систему записи любых чисел. Гипотеза Веселовского И.Н. (1959) Гипотеза Веселовского связана с применением двенадцатеричной системы счисления и счёта на пальцах (60 = 5×12, где 5 — число пальцев на руке) Гипотеза Кевича (1904) Кевич предпологает, что шестидесятеричная система возникла из смешения двух систем, существовавших прежде независимо: десятеричной и шестеричной. Одна из них, по мнению Кевича, должна быть система исчисления шумеров, другая - аккадян. Гипотеза мало обоснована фактами, оставляла открытым вопрос, какой из двух народов, шумерский или аккадский, имел первоначально шестиричную систему. Я считаю, что одна из самых правдивых гипотез у Нейгебауера. Ведь люди считая свои денежные средства, привыкали к этому виду подсчета и в итоге они привыкли считать именно по 60 шекелей. Любой подсчет каких либо вещей мог сравниваться с подщетом денег, ведь так было проще. В Древнем Вавилоне клинописные таблицы служили в качестве письма. Так же не существовало абстрактного понятия «универсальной единицы измерения». Каждый символ существовал только в связи со своим качественно-количественным признаком. Одна овца не равна одной мере зерна. Таким образом, первые символы письменности имели форму считаемых объектов (товаров). Например, знак «1 коза», «2 овцы», «3 меры зерна». Играя роль «символа-картинки», они по определению были пиктограммами. Священная Римская Империя Римская система дробей была связана с мерой веса, называемой «асс». Она делилась на 12 долей. 1/12 асса называлась унцией. Некоторые из них: семис — половина асса; секстанте — шестая доля асса; семиунция — пол-унции или 1/24 асса. Неудобство такой системы заключалось в невозможности представить число в виде дроби со знаменателем 10 или 100. С различными частями системы дробей мы встречаемся и повседневно. Например треть и унция. Треть – это 4 унции. Встречаем мы их ходя в магазин и говоря:<< можно мне треть батона>> Я считаю, что все системы дробей были хорошо развиты, ведь все они использовались для чего-то и многие используются даже сейчас. Например от Вавилонской шестидесятиричной системы пошел счет минут и часов ( по 60 минут), а некоторые части Римской системы мы используем и в повседневной жизни. |