урок 1. Понятие рационального числа

• Название: Понятие рационального числа
• Дата: 15.09.2022
• Размер: 173.06 Kb.
• Имя файла: урок 1 .docx
• Тип: Урок; #679074

Тарасова Н.Н.

Тема урока Понятие рационального числа
Тип урока Урок изучения нового материала.
Цели : Предметные:

·       Ввести понятие рационального числа;

·       Рассмотреть признак, который позволит объединить все известные в 6 классе числа в числа рациональные;

·       Совершенствовать вычислительные навыки учащихся.
Личностные: формировать умение представлять результат своей деятельности.
Метапредметные: формировать умение определять понятия, классифицировать, самостоятельно выбирать основания и критерии для классификации.
Планируемые результаты: Учащийся научиться распознавать рациональное число.
Основные понятия: целое число, дробное число, рациональное число.
Организационная структура урока

Этапы проведения урока	Форма организации УД		Задания для учащихся, выполнение которых приведет к достижению запланированных результатов
			Учебник		Дидактические материалы
1. Организационный этап
2. Постановка формируемых результатов и задач урока. Мотивация учебной деятельности учащихся
3. Актуализация знаний		Ф		Устно: Вопросы: Какие числа называются положительными? отрицательными? Какое число не положительно и не отрицательное?
4. Изучение нового материала		Ф		§31 (6 класс)
5. Первичное закрепление нового материала		Ф		№ 1; 2; 3; 4 ; - нечетные)
		И
7. Итоги урока				Какие числа называют рациональными? - Можно ли любое число представить в виде рационального? -Какими числами является сумма, разность, произведение рациональных чисел? - Всегда ли частное двух чисел является рациональным числом?
8. Информация о домашнем задании				§1,, № 5(1-2), №7 (1-2),- 7 кл П.16,17 ,31 № 883- 6 кл.

4. Изучение нового материала.

Итак, все числа можно разделить на целые и дробные.
Все натуральные числа, противоположные им числа и 0 называют целыми.
Т.е. целые числа делятся на положительные целые и отрицательные целые.
Дробные – это обыкновенные и десятичные дроби.

Объединив целые и дробные числа, мы получаем рациональные числа.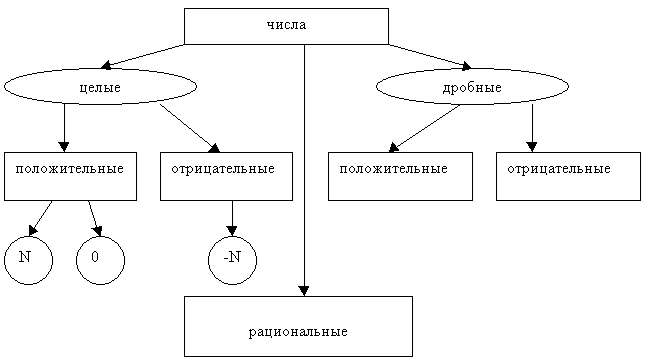



Определение: число, которое можно записать в виде  , где а – целое число, а n – натуральное число, называется рациональным числом.

Работая в группах, учащимся предлагается выполнить следующие задания:

Задание №1.

Какие из чисел 6; 0,17; 3 ; -8; -2 являются рациональными? Обсудите это в группах и обоснуйте ответ. Ответ: 6=  ; 0,17= ; 3 ;  ; 

Т.к все числа можно представить в виде  , где а – целое, n – натуральное, то все эти числа рациональные.

Задание №2

Представьте сумму, произведение, разность, частное в виде рационального числа:  ;  • ;  

После выполнения задания делаем вывод и в таблицу записываем, что сложение, умножение, вычитание и деление во множестве рациональных чисел выполняется всегда.

Задание №3

Представьте   в виде десятичной дроби двумя способами.

1. 
   Путем деления числителя на знаменатель.
   
2. 
   Используя основное свойство дроби, умножив числитель и знаменатель на 25.
   

При каком условии можно представить обыкновенную дробь в виде десятичной? (Если знаменатель можно представить как произведение двоек, или пятерок или двоек и пятерок).

Задание №4

Какие из дробей  можно представить в виде десятичной дроби и почему? Какие нельзя представить и почему?

Учитель: проверим домашнее задание, которое вы выполняли к сегодняшнему уроку.

На дом вам было задано представить дроби  в виде десятичных. Проверьте свои вычисления по данному образцу: 

Эти дроби в виде десятичной представить можно, если только разрешить писать бесконечные десятичные дроби. Т.к. в записях одна или несколько цифр повторяются, то такие дроби называются периодическими десятичными дробями. Записываются они так: 0,333…=0,(3); 0,4545…=0,(45). Используя образец, запишите две оставшиеся дроби.

Вывод: любое рациональное число можно записать в виде десятичной дроби или в виде периодической дроби или в виде целого числа.