1 лабораторная работа по теормеху_Аливохин_23632_1. Лабораторная работа 1 по теоретической механике Запишем математическую модель системы
 Скачать 490.26 Kb. Скачать 490.26 Kb.
|
|
Лабораторная работа №1 по теоретической механике
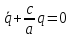 – Уравнение свободных колебаний – Уравнение свободных колебаний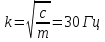 – Собственная частота колебаний – Собственная частота колебаний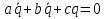 – Уравнение колебаний с трением, b – коэффициент сопротивления – Уравнение колебаний с трением, b – коэффициент сопротивления
Свободные колебания без сопротивления для двух значений амплитуд колебаний: 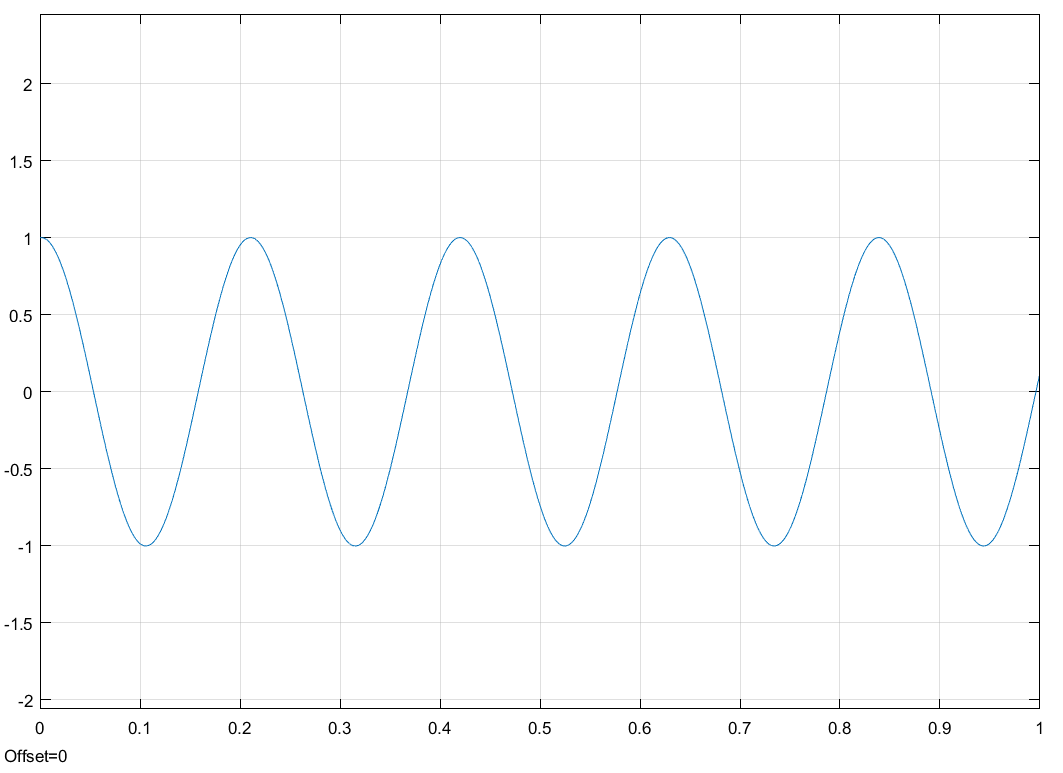 Рисунок 1. Свободные колебания при 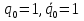 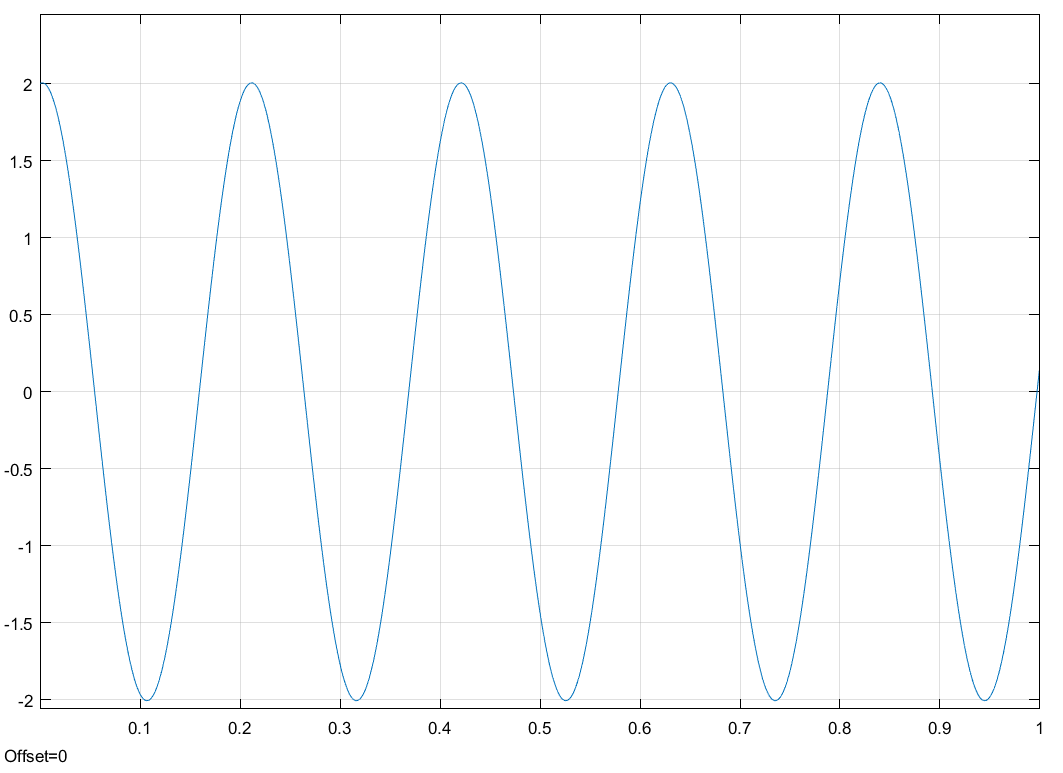 Рисунок 2. Свободные колебания при 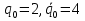 Вывод: По полученным графикам делаем вывод, что амплитуда не влияет на собственную частоту и период колебаний. Период колебаний без вязкого трения: 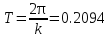 Замечание 1: оценим период колебаний по графику, сравним с расчетным значением. Период по графику: 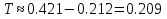 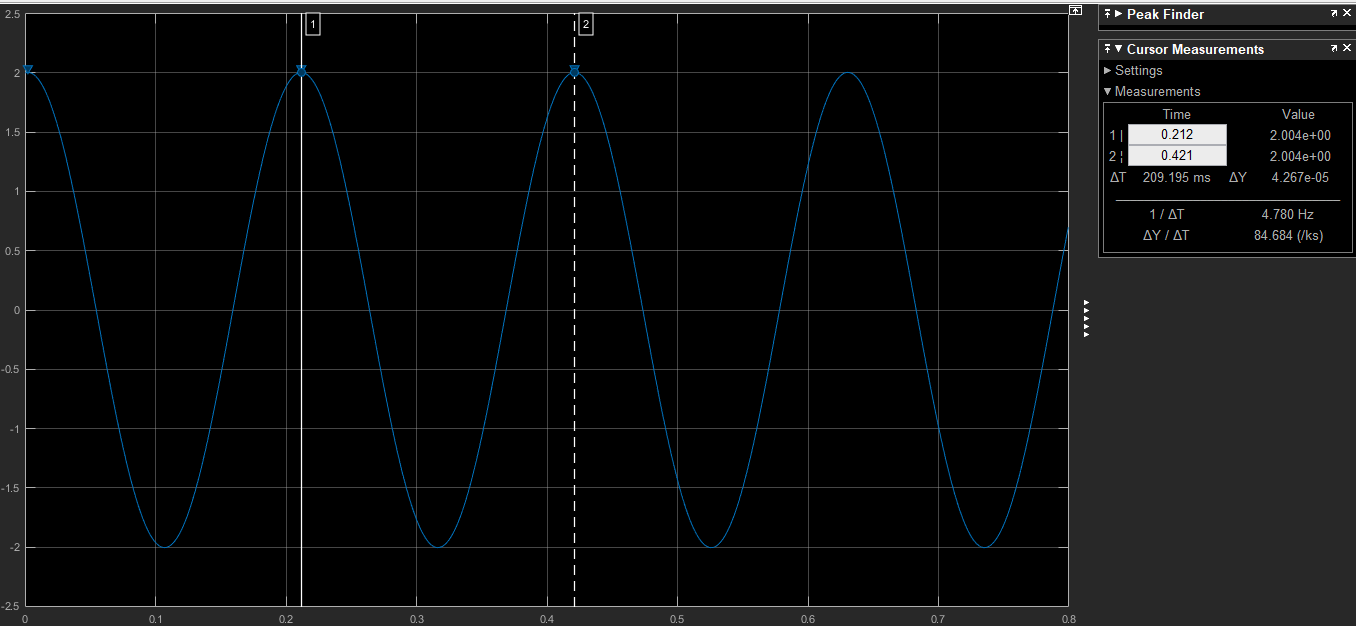 Расчетный период: 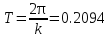 Вывод: Расчетный период совпадает с периодом, определенным по графикам с точностью до тысячных. Свободные колебания для двух значений коэффициента сопротивления: 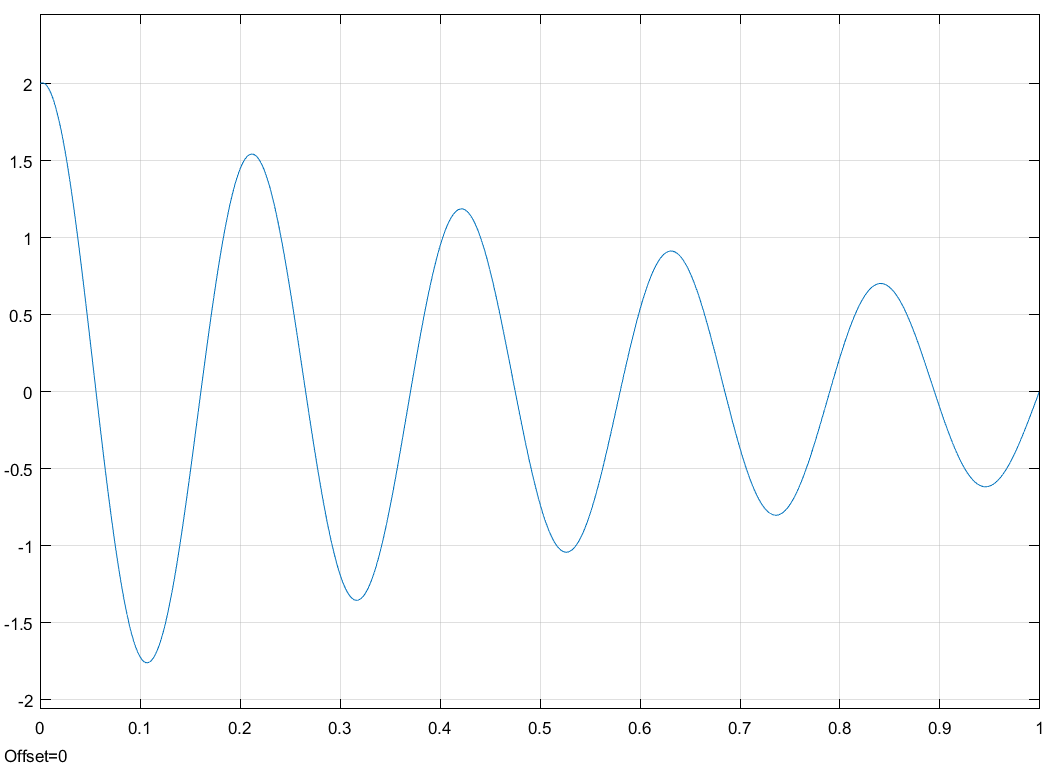 Рисунок 3. Свободные колебания системы при значении коэффициента сопротивления b=10 Период колебаний при b = 10: 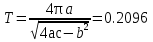 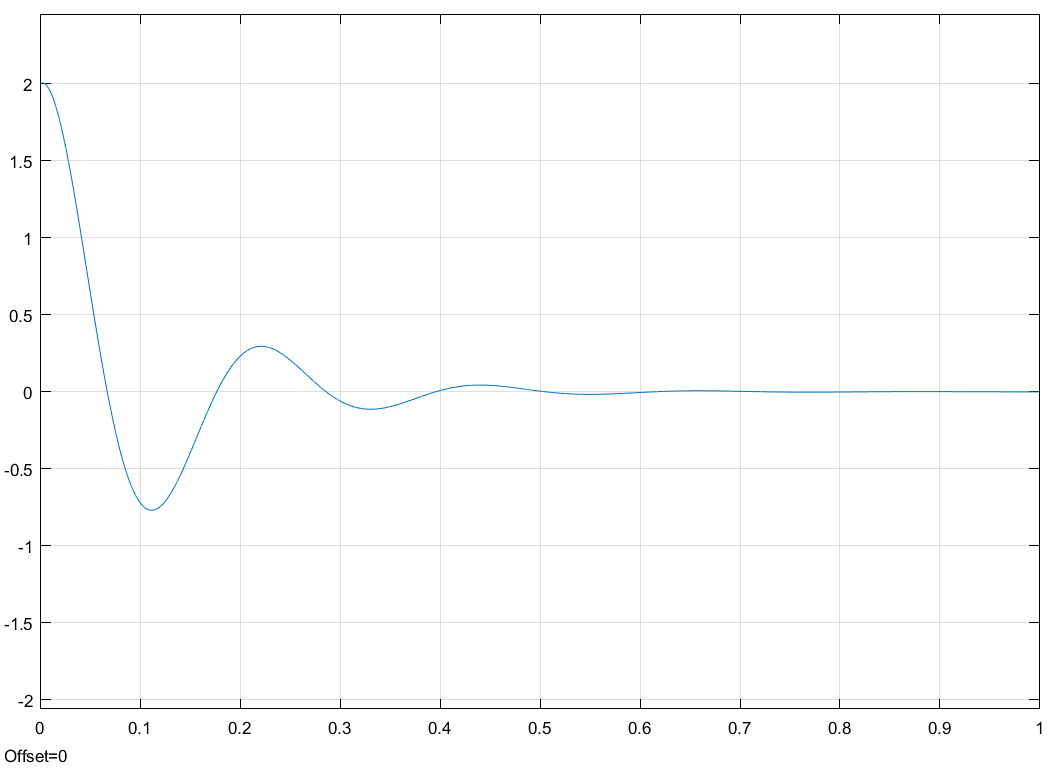 Рисунок 4. Свободные колебания системы при значении коэффициента сопротивления b=70 Период колебаний при b = 70: 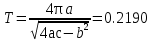 Вывод: видно, что период изменяется несильно. Колебания – затухающие. При увеличении демпфирования амплитуда уменьшается. И по графикам амплитуда уменьшается по экспоненте. Замечание 2: оценим скорость убывание амплитуды для двух значений коэффициента сопротивления 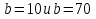 Для этого нужно оценить амплитуды колебаний на двух соседних периодах по графику и найти их отношение. Для 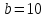 : : 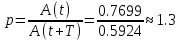 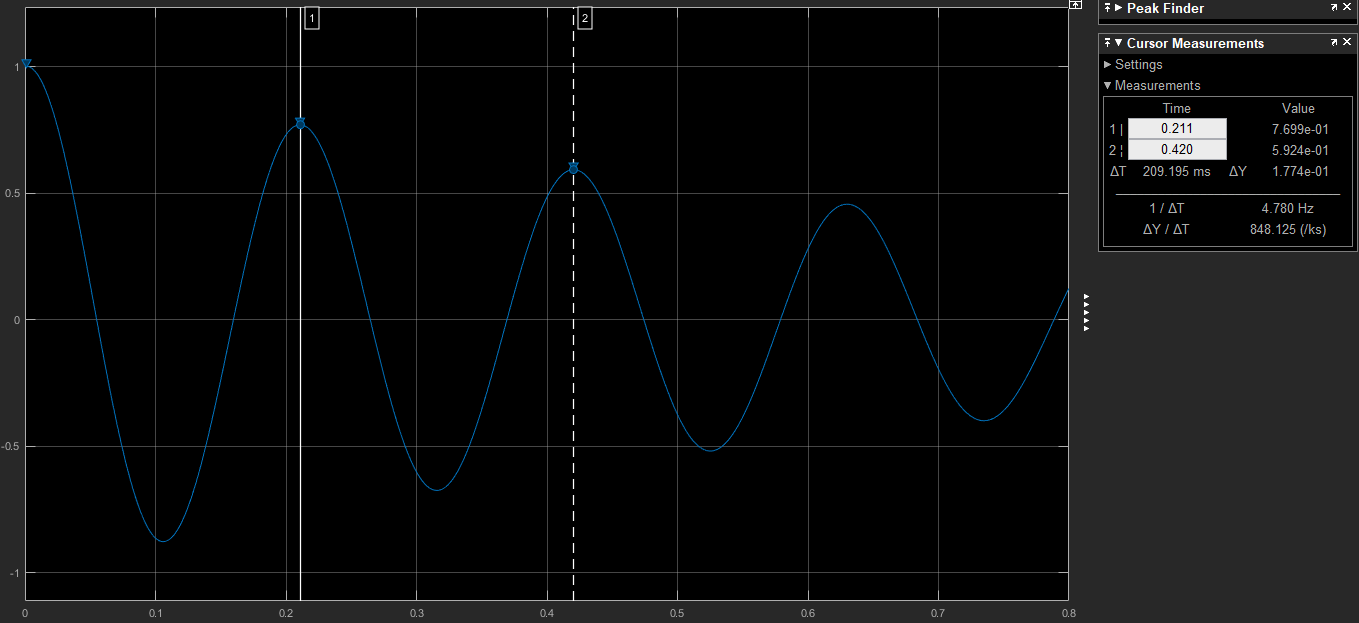 Для 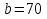 : : 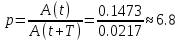 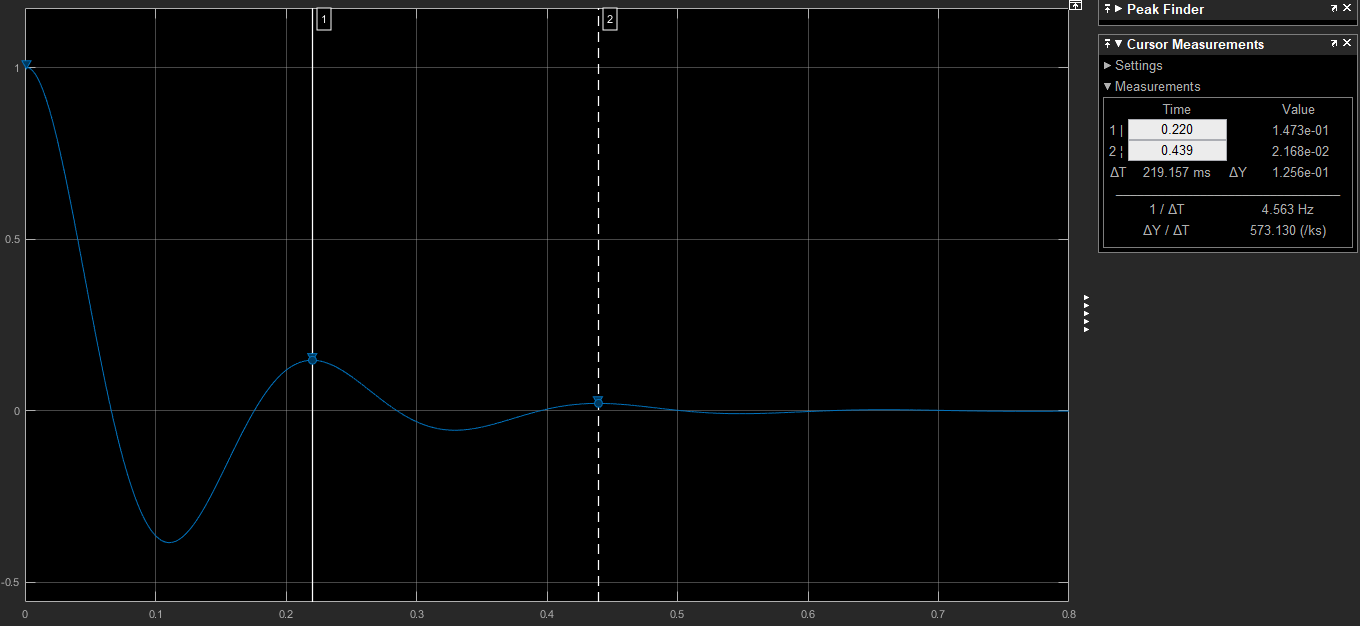 Теперь сравним их с расчетным значением: Для 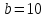 : : 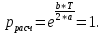 2995 2995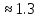 Для 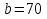 : : 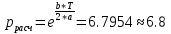 Вывод: расчетная скорость убывания амплитуды совпадает с определенной по графика с точностью до десятых. Резонанс системы без сопротивления для двух значений амплитуды возмущающей силы: 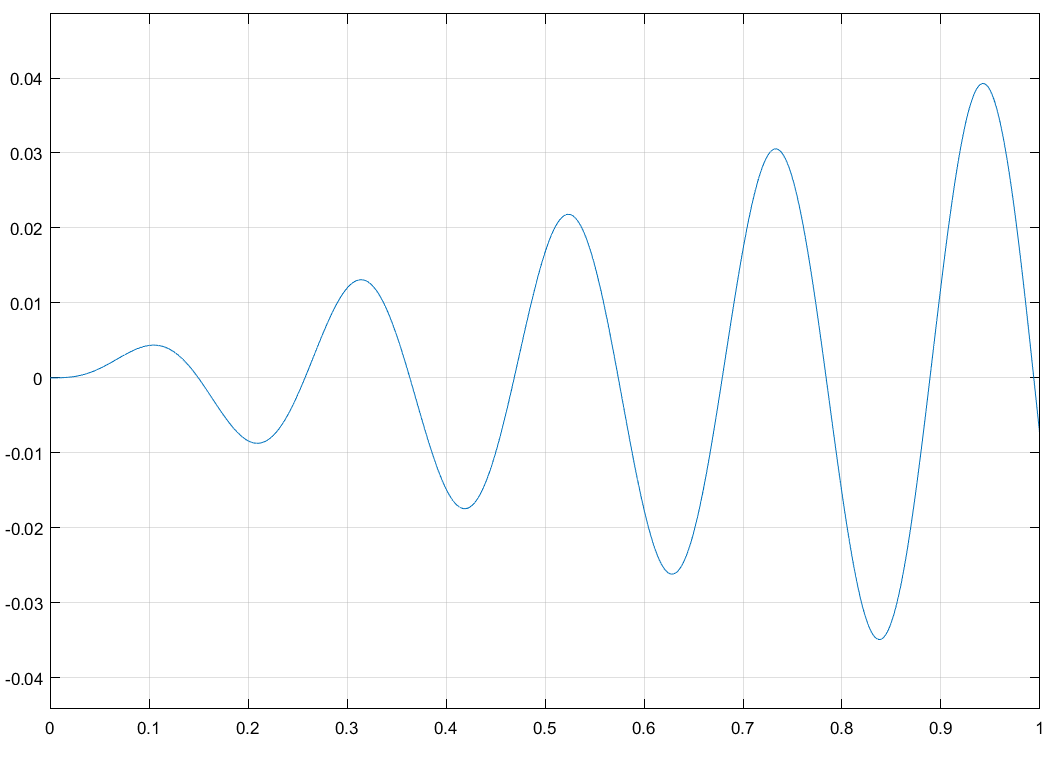 Рисунок 5. Резонанс системы без сопротивления при значении амплитуды 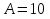 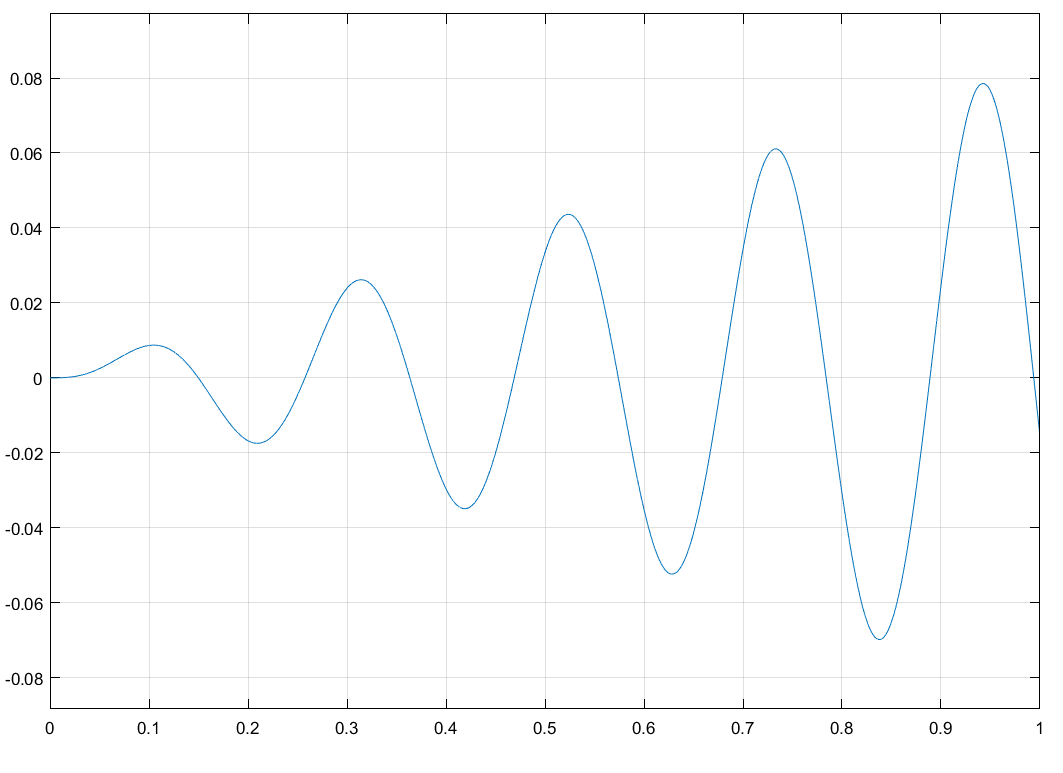 Рисунок 6. Резонанс системы без сопротивления при амплитуде 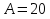 Вывод: По полученным графикам видно, что амплитуда колебаний линейно зависит от амплитуды вынуждающей силы. Резонанс системы при учете сопротивления для двух значений коэффициента сопротивления. 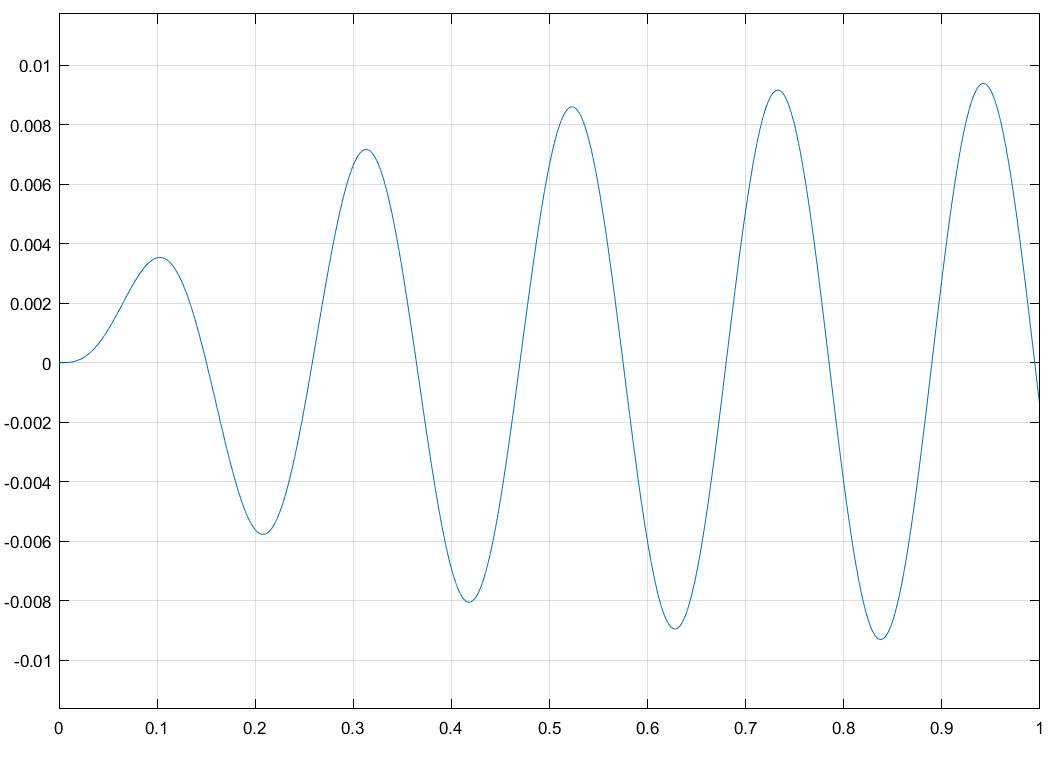 Рисунок 7. Резонанс системы с учетом сопротивления при коэффициенте сопротивления 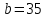 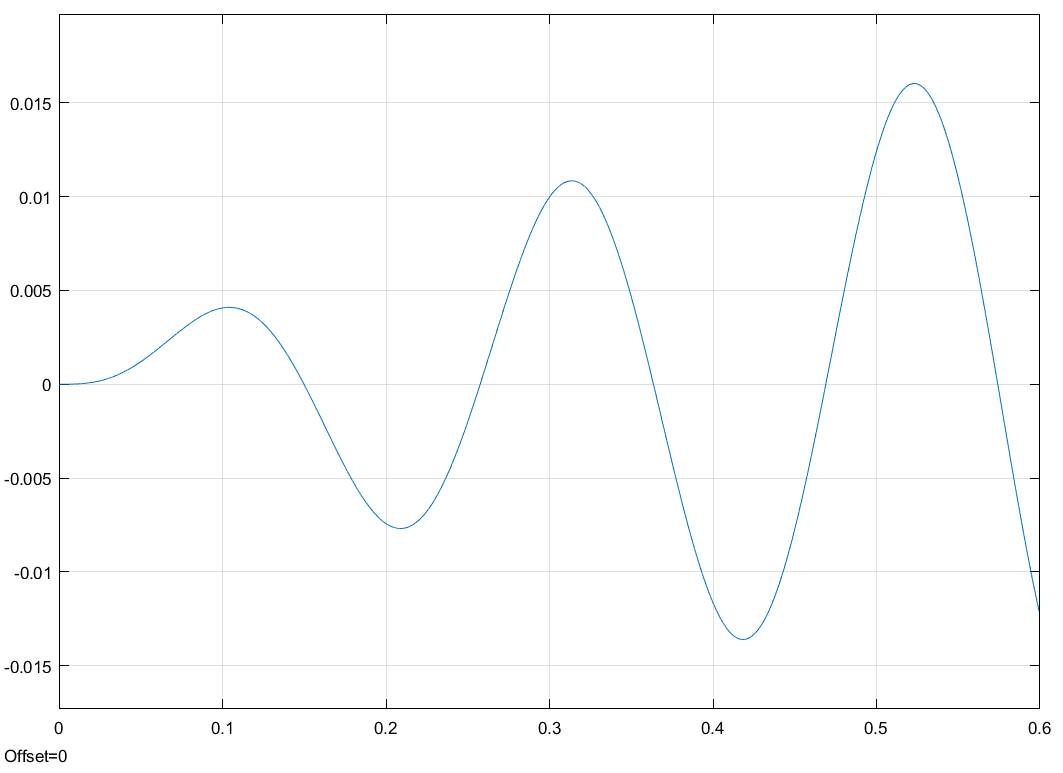 Рисунок 8. Резонанс системы с учетом сопротивления при коэффициенте сопротивления 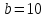 Вывод: По данным графикам можно сделать вывод, что при сопротивлении системы резонанс достигается до определенной амплитуды. При увеличении коэф. сопротивления в два раза амплитуда колебаний уменьшилась примерно в два раза. Биения системы для колебаний без учета сопротивления и для системы с сопротивлением: 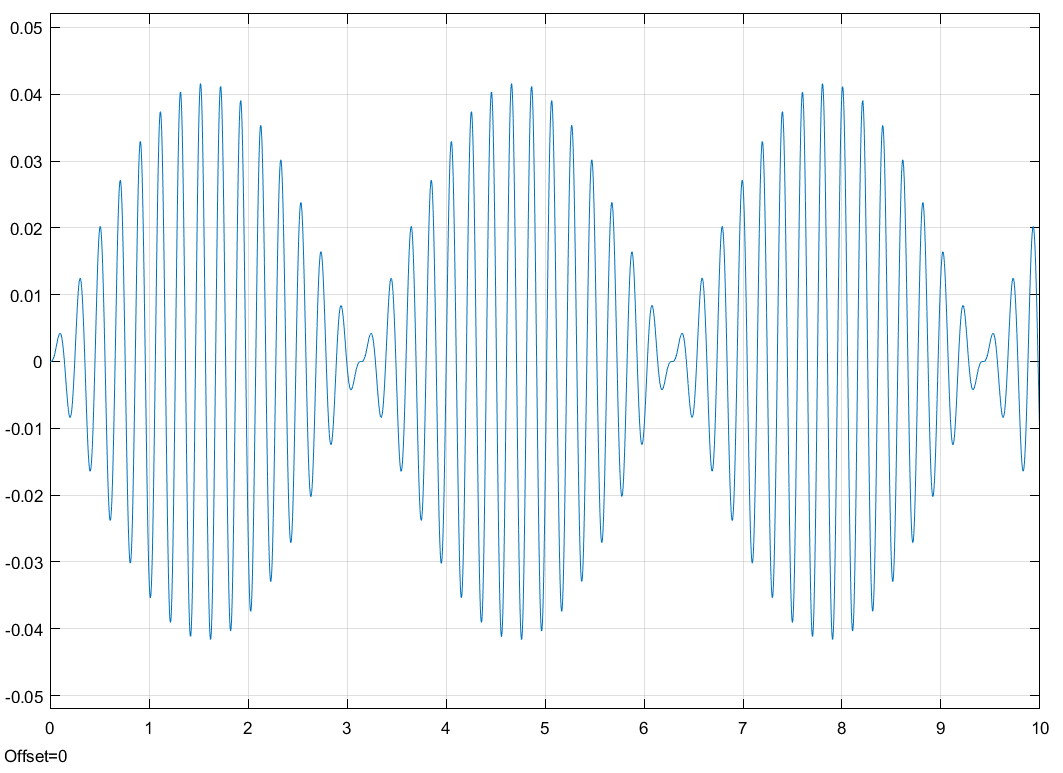 Рисунок 9. Биение системы без учета сопротивления 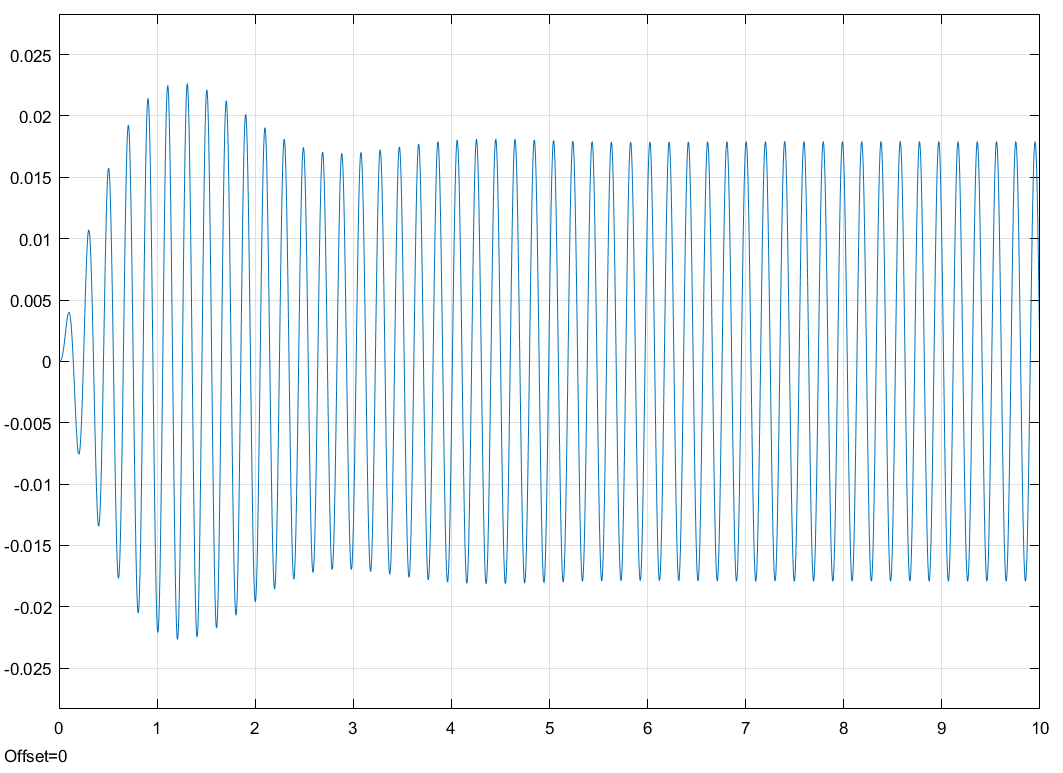 Рисунок 10. Биения системы с учетом сопротивления 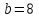 Вывод: По полученным графикам можно сказать, что при наличии сопротивления амплитуда биения уменьшается и в конце концов биения прекращаются. |
