ФУНКЦИЯ БЛОХА. .Функция Блоха. Реферат По дисциплине Физика твердого телаатомовмолекулнано На тему Функция Блоха
 Скачать 0.52 Mb. Скачать 0.52 Mb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ УЧРЕЖДЕНИЕ ….. Институт …. Реферат По дисциплине: «Физика твердого тела/атомов/молекул/нано» На тему: «Функция Блоха» Выполнил: Студент (_) курса, (_) группы Фамилия, Имя, Отчество Научный руководитель: (Должность, название кафедры) Фамилия, Имя, Отчество Оценка _____________________ Дата ________________ Подпись ____________________ …2020 ОглавлениеВведение 2 1. Общие представления о Феликсе Блохе и его научном вкладе 5 2. Функция Блоха 6 3. Метод вычисления блоховских функций 9 Заключение 16 Список использованной литературы 17 ВведениеАктуальность темы. Как известно, твердые тела – металлы и полупроводники – представляют собой многочастичные системы: в них электроны движутся в поле ядер и взаимодействуют друг с другом. Однако часто можно оправдать приближение самосогласованного поля, согласно которому движение выделенного электрона можно рассматривать в сглаженном поле других частиц. В этом случае применимо одноэлектронное приближение, а для расчета волновой функции электрона можно использовать одночастичное приближение, когда потенциал определяется периодической плотностью зарядов – периодической функцией. Согласно теореме Блоха состояние электронов с энергией, принадлежащей разрешенной зоне, описываются блоховской волновой функцией, представляющей собой произведение периодической функции на плоскую волну. Аналитический расчет блоховских функций возможен только для определенного класса модельных потенциалов, поэтому необходимо использовать численные методы для получения результатов. Феликс Блох (1905-1983) – один из основоположников современной физики. Лауреат Нобелевской премии по физике за создание теории ядерного магнитного резонанса (1952). Поэтому данная тема имеет высокую социальную значимость и актуальна для современной науки. Объект исследования – квантовомеханическая теория движения электронов в твёрдом теле. Предмет исследования – функция Феликса Блоха. Цель данной работы – выявить вклад Феликса Блоха в науку и показать простой численный метод расчета блоховских функций. Для выполнения цели работы были поставлены следующие задачи: рассмотреть общие представления о Феликсе Блохе и его научном вкладе; проанализировать функцию Блоха; выявить наиболее подходящий метод вычисления блоховских функций. Обзор литературы. Важнейшем трудом в работе есть книга Ф. Блоха «О квантовой механике электронов в кристаллических решетках»; значительными оказались работы П.В. Павлова «Статистическая физика» (часть 2); А.Ф. Хохлова «Физика твердого тела»; З. Флюгге «Задачи по квантовой механике» (том 1); Н. Акшрофта «Физика твердого тела» (том 1). Структура исследования. Реферат состоит из введения, трёх глав, заключения, списка использованной литературы. Общее количество страниц – 17. Практическое использование. Результаты работы могут быть полезны для студентов специальности «Физика», «Нанотехнология», «Электроника и микроэлектроника», и для специализирующихся в области физики наноструктур. 1. Общие представления о Феликсе Блохе и его научном вкладе Феликс Блох (1905-1983) – один из основоположников современной физики. Лауреат Нобелевской премии по физике за соз-дание теории ядерного магнитного резонанса (1952). Р  одился в Цюрихе (Швейцария). Высшее образование получил в высшей технической школе Цюриха. Поступал на инженерное отделение, но вскоре перешёл на физическое. Получив диплом в 1927 году, продолжил обучение в Лейпцигском университете, получив докторскую степень (эквивалентна кандидату физ.-мат. наук) в 1928 году. Продолжил заниматься наукой в Германии, вместе с Гейзенбергом, Паули, Бором и Ферми. Будучи евреем, Блох покинул Германию как только нацисты пришли к власти в 1933 году. Вначале направился в Цюрих, а затем в Париж, где некоторое время преподавал в Институте Пуанкаре. одился в Цюрихе (Швейцария). Высшее образование получил в высшей технической школе Цюриха. Поступал на инженерное отделение, но вскоре перешёл на физическое. Получив диплом в 1927 году, продолжил обучение в Лейпцигском университете, получив докторскую степень (эквивалентна кандидату физ.-мат. наук) в 1928 году. Продолжил заниматься наукой в Германии, вместе с Гейзенбергом, Паули, Бором и Ферми. Будучи евреем, Блох покинул Германию как только нацисты пришли к власти в 1933 году. Вначале направился в Цюрих, а затем в Париж, где некоторое время преподавал в Институте Пуанкаре. В 1934 году получает приглашение на должность профессора теоретической физики из Стэнфордского университета, которое он принимает и в тот же год переезжает в США. С кафедрой физики Стэнфорда связана вся дальнейшая научная деятельность Блоха — здесь он проработает до самой смерти, не считая двух перерывов. Первого, во время Второй мировой войны, когда он работал над военными проектами, и второго, в 1954—1955 годах, когда был приглашён на пост первого генерального директора Европейской лаборатории ядерных исследований (ЦЕРН). В 1939 году стал гражданином США. Во время Второй мировой войны начал работу над атомным проектом в Лос-Аламосе, однако, спустя некоторое время перешёл в радарный проект в Гарвардском университете. После войны вернулся в Стэнфорд и возобновил работу над предвоенной темой. За создание теории ядерного магнитного резонанса Ф. Блох совместно с Э. М. Парселлом в 1952 году был удостоен Нобелевской премии по физике «за развитие новых методов для точных ядерных магнитных измерений и связанные с этим открытия». 2. Функция БлохаФ  еликс Блох в 1928 году [1] доказал замечательную теорему, которая лежит в основе одноэлектронной теории твердых тел [2-6]. Согласно теореме Блоха, волновые функции, являющиеся решениями одноэлектронного уравнения Шредингера (1.1) еликс Блох в 1928 году [1] доказал замечательную теорему, которая лежит в основе одноэлектронной теории твердых тел [2-6]. Согласно теореме Блоха, волновые функции, являющиеся решениями одноэлектронного уравнения Шредингера (1.1)  (1.1) с периодическим потенциалом, имеющим период решетки, представляют собой плоские волны, модулированные периодической функцией, то есть Здесь З г В векторы единичных трансляций; И У Действительно, Естественно, что показатель степени экспоненты должен быть безразмерной величиной. Поскольку М  одуль вектора одуль вектора С 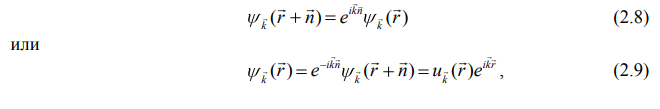 учетом (2.6) перепишем (2.4) в виде учетом (2.6) перепишем (2.4) в видездесь через я 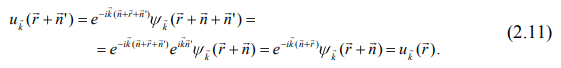 вляющаяся периодической с периодом решетки. В силу (2.8) и (2.10) имеем вляющаяся периодической с периодом решетки. В силу (2.8) и (2.10) имеемТаким образом, действительно, волновая функция электрона в кристалле представляет собой стоячую волну 3. Метод вычисления блоховских функцийДля вычисления блоховских функций развиты различные методы, подробно изложенные в научной литературе. В данном разделе мы изложим оригинальный метод численного решения уравнения Шредингера для электрона в одномерном периодическом потенциале. Достоинство метода – простота, легкость программирования и численная устойчивость. Пусть мы имеем одномерный периодический потенциал V(x+a)=V(x). Удобно считать, что ионы покоятся в точках минимума потенциала V(x), которые, по предположению, определяют нулевые значение энергии. Будем рассматривать периодический потенциал как суперпозицию потенциальных барьеров v(x) c шириной а, центры которых находятся в точках x=± na: 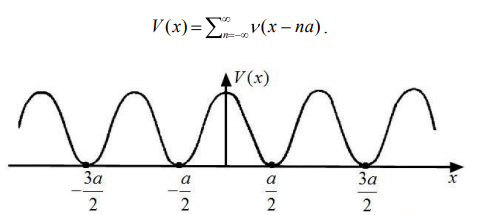  (3.1)  Рис.3.1. Одномерный периодический потенциал V(x) К 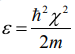 аждое слагаемое v(x-na) представляет собой потенциальный барьер, сквозь который электрон может туннелировать, переходя от иона к иону. Сначала предположим, что v(x)= v(-x). Попытаемся выразить блоховские функции и закон дисперсии через характеристики отдельного барьера v(x). Рассмотрим электрон, падающий слева на потенциальный барьер и имеющий энергию аждое слагаемое v(x-na) представляет собой потенциальный барьер, сквозь который электрон может туннелировать, переходя от иона к иону. Сначала предположим, что v(x)= v(-x). Попытаемся выразить блоховские функции и закон дисперсии через характеристики отдельного барьера v(x). Рассмотрим электрон, падающий слева на потенциальный барьер и имеющий энергию Для него справедливо уравнение Шредингера: 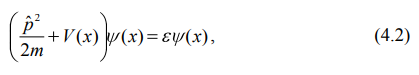  (3.2) п 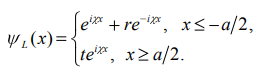 оскольку v(x)=0 при В этих областях волновая функция оскольку v(x)=0 при В этих областях волновая функция  (3.3) Схематически процесс рассеяния изображен на рис.3.2. 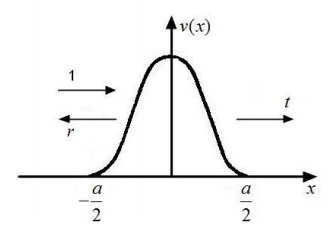  Рис. 3.2. Частицы, падающие слева на один из барьеров К  оэффициенты прохождения t, t’ и отражения r, r’ входят в так называемую матрицу рассеяния [8, 9] оэффициенты прохождения t, t’ и отражения r, r’ входят в так называемую матрицу рассеяния [8, 9]Из закона сохранения потока вероятности находим Отсюда можно получить: Если написать то нетрудно показать что Коэффициенты прохождения t и отражения r дают амплитуду вероятности того, что электрон протуннелирует сквозь барьер или отразиться от него, соответственно. Зависимость амплитуд рассеяния от волнового 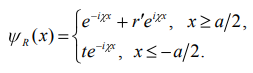  (3.4) вектора Эта функция описывает частицу, которая падает на барьер справа рис. 3.3. 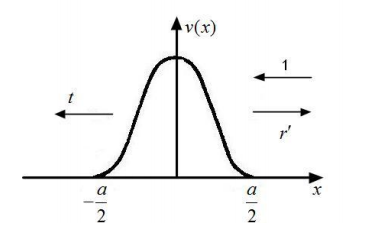  Рис. 3.3. Частицы, падающие справа на один из барьеров. Так как Дифференцируя (3.6), находим также, что производная 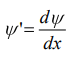 должна удовлетворять условию: должна удовлетворять условию:Налагая условия (3.6) и (3.7) при Подставим в (3.8) и (3.9) вид функции (3.5)  (3.10) 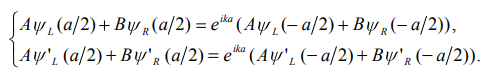 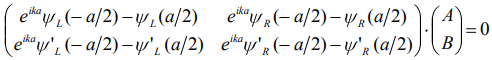 И У 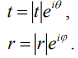 О Докажем формулу (3.14) проведя следующий мысленный эксперимент 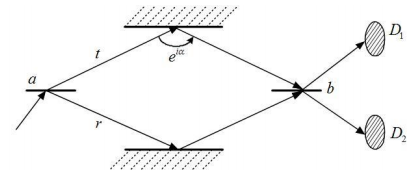  Рис. 3.4.Схема мысленного эксперимента П 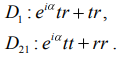 усть имеется два полупрозрачных зеркала a и b, два экрана и соответственно два детектора (рис.3.4). Если на полупрозрачное зеркало а падает электронный пучок, то часть пучка зеркало пропустит и часть отразит с амплитудами t и r. На верхнем экране пучок наберет фазу усть имеется два полупрозрачных зеркала a и b, два экрана и соответственно два детектора (рис.3.4). Если на полупрозрачное зеркало а падает электронный пучок, то часть пучка зеркало пропустит и часть отразит с амплитудами t и r. На верхнем экране пучок наберет фазу Воспользуемся условием, что сумма вероятностей прохождения и отражения должна быть равна единице: Используя выражения (3.15) и (3.16): П Итак, энергия и волновой вектор блоховского электрона связаны между собой следующим образом: 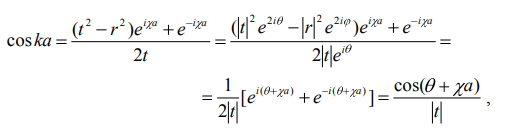 т 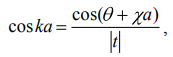 п 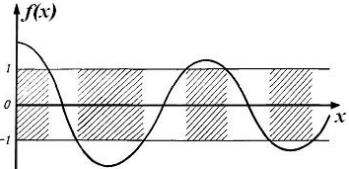  Рис. 3.5. Характерный вид функции Д 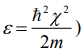 а 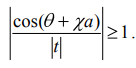 запрещенные зоны имеют место для энергий в интервале, определяемом неравенством запрещенные зоны имеют место для энергий в интервале, определяемом неравенствомЕ 1 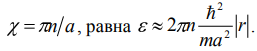 )Если барьер является очень «слабым» (т.е. что ). В этом случае энергетические щели очень узкие, а ширина щели содержащей )Если барьер является очень «слабым» (т.е. что ). В этом случае энергетические щели очень узкие, а ширина щели содержащей2)Если барьер очень «сильный», так что , тогда разрешенные зоны энергий очень узкие. О 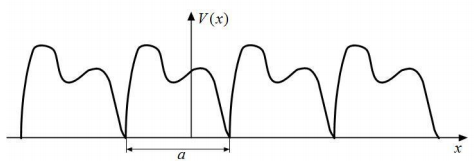 бобщим предыдущую задачу на случай периодического потенциала общего вида (см. рис. 3.6). Хотя рассеяние на потенциале элементарной ячейки отличается от проделанного выше (отсутствует соотношение (3.14) для фаз коэффициентов отражения и прохождения), аналогичные вычисления все равно приводят к дисперсионному соотношению (3.19). бобщим предыдущую задачу на случай периодического потенциала общего вида (см. рис. 3.6). Хотя рассеяние на потенциале элементарной ячейки отличается от проделанного выше (отсутствует соотношение (3.14) для фаз коэффициентов отражения и прохождения), аналогичные вычисления все равно приводят к дисперсионному соотношению (3.19). Рис. 3.6. Периодический потенциал не обладающий центром инверсии Совпадение результатов объясняется тем, что в силу симметрии относительно обращения времени должно выполняться соотношение ЗаключениеВ реферате были выявлены некоторые основные моменты биографии Феликса Блоха, что дало возможность узнать целостную картину о появлении функции Блоха. Сам Блох родился в Цюрихе (Швейцария). Высшее образование получил в высшей технической школе Цюриха. На этом он не останавливается, и получает образование в лучших университетах Европы и Америки. В дальнейшем вся его жизнь связана с кафедрой физики Стэнфордского университета, военными проектами и опытами. В результате, за создание теории ядерного магнитного резонанса Ф. Блох совместно с Э. М. Парселлом в 1952 году был удостоен Нобелевской премии по физике «за развитие новых методов для точных ядерных магнитных измерений и связанные с этим открытия». Далее в работе рассмотрена задача о движении электрона в одномерном периодическом потенциале. Обсуждаются основные приближения, которые делаются при формулировке одноэлектронного уравнения Шредингера, приводится простое доказательство теоремы Блоха и основные свойства закона дисперсии для электрона в периодическом потенциале. В ходе решении последней задачи нами формулируется метод расчета блоховских функций на основе матрицы рассеяния. Таким образом, в ходе исследования удалось достичь назначенной цели и выполнить поставленные задачи. Список использованной литературы1. Bloch F. Über die Quantenmechanik der Elektronen in Kristallgittern// Z. Phys., v. 52, p. 555 (1928). 2. Питаевский Л.П., Лифшиц Е.М. Статистическая физика (часть 2). – М.: Физматлит, 2004. 3. Павлов П.В., Хохлов А.Ф. Физика твердого тела. – Н.Н.: ННГУ, 1993. 4. Киттель Ч. Введение в физику твердого тела. – М.: МедиаСтар, 2006. 5. Флюгге З. Задачи по квантовой механике (том 1). – М.: Мир, 1974. 6. Акшрофт Н., Мермин Н. Физика твердого тела (том 1). – М.: Мир, 1979. 7. Кrоnig R. de L., Penney W. G. Quantum mechanics of electrons in crystal lattices // Proc. Roy. Soc. London, v. 130A, p. 499 (1931). 8. Ландау Л.Д., Лифшиц Е.М. Квантовая механика (Нерелятивистская теория). – М.: Физматлит, 2002. 9. Сатанин А.М. Численные методы в нанофизике. – Н.Н.: ННГУ, 2006. |
