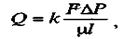шаблон. Shablon_referata — копия. Реферат по курсу Основы нефтегазового дела

• Название: Реферат по курсу Основы нефтегазового дела
• Анкор: шаблон
• Дата: 07.07.2020
• Размер: 65.47 Kb.
• Имя файла: Shablon_referata — копия.odt
• Тип: Реферат; #133928

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

ФГБОУ ВО «УДМУРТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

Институт нефти и газа им. М.С. Гуцериева

Кафедра разработки и эксплуатации нефтяных и газовых скважин

Реферат

по курсу «Основы нефтегазового дела»

Приток жидкости к скважине. Воронка депрессии

Выполнил:

студент группы ОПБ- 21.03.01-11

Ворончихин А.С.

Проверил:

старший преподаватель кафедры «РЭНГМ»

Миронычев В.Г.
Ижевск

2018 г.
СОДЕРЖАНИЕ

Приток жидкости к скважине. Воронка депрессии 1

Приток жидкости к скважине 6

Введение

При вставке текста или объектов рекомендую вставлять фрагменты, не сохраняя исходные форматы, т.е. используя специальную вставку без сохранения форматов исходных документов.

Вступительная часть реферата, помещаемая перед основным текстом. Оно должно содержать общий обзор использованной литературы, цель работы.

Объем введения примерно 1-1,5 страницы (примерно 1/10 часть от всего объема реферата).

Требования к оформлению и содержанию могут изменяться. Не все требования к оформлению, приведенные в шаблоне, соответствуют ГОСТ 7.32 [1].
При отборе жидкости (газа) из скважины в пласте двигаются (фильтруются) пластовые флюиды. Движение флюидов в пласте проходит по радиальным направлениям. Если жидкость движется к центру скважины (отбирается из потока), то это - сток - добывающая, эксплуатационная скважина. Если жидкость движется в обратном направлении (добавляется к потоку), это - источник - нагнетательная скважина.

По мере приближения к скважине при условии постоянной величины отбора продукции из скважины, постоянной толщины и однородной проницаемости, скорости фильтрации (движения) флюидов возрастает, достигая максимума у стенки скважины.

Как правило скважины не бывают гидродинамически совершёнными. Так, в некоторых скважинах вскрывают только часть толщины пласта, и если пласт не крепят обсадной колонной, то такие скважины являются несовершёнными по степени вскрытия.

В большинстве скважин пласт вскрывают на всю его толщину, но сообщение скважины с пластом осуществляется через ограниченное число отверстий в обсадной колонне. Такие скважины несовершенны по характеру вскрытия. Чаще всего в производственной практике скважины по степени и характеру вскрытия одновременно.

Очевидно, что любое несовершенство скважин приводит к возникновению дополнительных фильтрационных сопротивлений в призабойной зоне пласта вследствие отклонения течения жидкостей (газа) от плоскорадиального потока и разного возрастания скорости их течения у перфорационных отверстий.

Отношение дебита Q несовершенной скважины к дебиту Q совершенной скважиной называют коэффициентом совершенства ф:

Коэффициент ф характеризует состояние ПЗП при соответствующей технике и технологии вскрытия пласта бурением (первичное и перфорацией (вторичное)).

Вокруг каждой работающей скважины в процессе бурения, эксплуатации образуется воронка:

депрессии - в добывающей, эксплуатационной;

репрессии - в нагнетательной.

Депрессионная воронка - это поверхность, образованная логарифмической кривой распределения давления вокруг оси скважины.

В пределах воронки депрессии градиенты давления, а значит и расходы энергии на единицу длины пути резко возрастают по мере приближения к скважине. Значительная доля перепада давления в пласте расходуется в непосредственной близости от скважины. По мере удаления от скважины кривые градиентов давления значительно выравниваются, что указывает на резкое уменьшение скорости фильтрации с удалением от скважины.

Приток жидкости к скважине

Приток жидкости, газа, воды или их смесей к скважинам происходит в результате установления на забое скважин давления меньшего, чем в продуктивном пласте. Течение жидкости к скважинам исключительно сложно и не всегда поддается расчету. Лишь при геометрически правильном размещении скважин (линейные или кольцевые ряды скважин и правильные сетки), а также при ряде допущений (постоянство толщины, проницаемости и других параметров) удается аналитически рассчитать дебиты этих скважин при заданных давлениях на забоях или, наоборот, рассчитать давление при заданных дебитах. Однако вблизи каждой скважины в однородном пласте течение жидкости становится близким к радиальному. Это позволяет широко использовать для расчетов радиальную схему фильтрации.

Скорость фильтрации, согласно закону Дарси, записанному в дифференциальной форме, определяется следующим образом:



(2.4)

где k - проницаемость пласта; μ - динамическая вязкость; dp/dr - градиент давления вдоль радиуса (линии тока).

По всем линиям тока течение будет одинаковое. Другими словами, переменные, которыми являются скорость фильтрации и градиент давления, при изменении угловой координаты (в случае однородного пласта) останутся неизмененными, что позволяет оценить объемный расход жидкости q как произведение скорости фильтрации на площадь сечения пласта. В качестве площади может быть взята площадь сечения цилиндра 2πrh произвольного радиуса r, проведенного из центра скважины, где h - действительная толщина пласта, через который происходит фильтрация.

Тогда



. (2.5)



Обозначим

В общем случае предположим, что ε - гидропроводность - изменяется вдоль радиуса r, но так, что на одинаковых расстояниях от оси скважины вдоль любого радиуса величины ε одинаковые. Это случай так называемой кольцевой неоднородности.

Предположим, что ε задано в виде известной функции радиуса, т. е.



. (2.6)

Вводя (2.6) в (2.5) и разделяя переменные, получим



. (2.7)

Дифференциальное уравнение (2.7) с разделенными переменными может быть проинтегрировано, если задана функция ε(r). В частности, если гидропроводность не зависит от радиуса и постоянна, то (2.7) легко интегрируется в пределах области фильтрации, т. е. от стенок скважины rс с давлением Pс до внешней окружности Rк, называемой контуром питания, на котором существует постоянное давление Pк. Таким образом,

,

При ε = const будем иметь

. (2.9)

Решая (2.9) относительно q, получим классическую формулу притока к центральной скважине в круговом однородном пласте:



. (2.10)

Если (2.8) проинтегрировать при переменных верхних пределах r и P, то получим формулу для распределения давления вокруг скважины:



. (2.12)

После интегрирования, подстановки пределов и алгебраических преобразований имеем

. (2.12)

Решая уравнение относительно р(r) и подставляя (2.10) в (2.12), получим уравнение распределения давления вокруг скважины:

. (2.13)

Если в (2.8) в качестве переменных пределов принять не верхние, а нижние пределы, то выражение для р(r) можно записать в другом виде:



. (2.14)

Подставляя в (2.13) или (2.14) Rк вместо переменного радиуса r, получим P(Rк) = Pк ; при r = rс имеем другое граничное условие:

P(rc) = Рс.

Таким образом, граничные условия выполняются. Из (2.13) и (2.14) следует, что функция P(r) является логарифмической, т. е. давление вблизи стенок скважины изменяется сильно, а на удаленном расстоянии - слабо. Это объясняется увеличением скоростей фильтрации при приближении струек тока к стенкам скважины, на что расходуется больший перепад давления.

Рассмотрим случай радиального притока в скважину при произвольно изменяющейся вдоль радиуса гидропроводности.

Проинтегрируем в (2.8) правую часть и перепишем результат следующим образом:

. (2.15)

Подынтегральная функция

. (2.16)

может быть построена графически по заданным значениям ε для различных радиусов и проинтегрирована в пределах от rс до Rк любым методом приближенного интегрирования или измерением планиметром площади под кривой у(r) в заданных пределах.

В некоторых случаях добывающая скважина дренирует одновременно несколько пропластков с различными проницаемостями, толщинами, вязкостями нефти, а также пластовыми давлениями. Однако приток в такой сложной системе будет происходить при одинаковом забойном давлении (приведенном). При этом некоторые пропластки с меньшим пластовым давлением, чем на забое скважины, способны поглощать жидкость. В любом случае общий приток такого многослойного пласта будет равен алгебраической сумме притоков из каждого пропластка:

. (2.17)

Формулы радиального притока, вследствие их простоты, часто используются в инженерных расчетах. При этом погрешности в оценке исходных параметров, таких как k, h, μ, (Pк - Pс), непосредственно влияют на величину q. Что касается величин Rк и rс, то, поскольку они находятся под знаком логарифма, в отношении их допустимы значительные погрешности.

Пример. Допустим истинное значение Rк = 100 м, а в расчете по ошибке было принято Rк = 1000 м, т. е. допущена 10-кратная ошибка. Тогда истинный приток

, (2.18)

где rc = 0,1 м.

Расчетный приток

. (2.19)

Сравнение производим при прочих равных условиях, деля (2.18) на (2.19):

. (2.20)

Откуда qрасч = 3/4 qист. Т. е. расчетный дебит будет составлять 75% истинного дебита.

При применении формулы радиального притока для скважины, расположенной среди других добывающих скважин, за Rк принимают половину расстояния до соседних скважин или средневзвешенную по углу величину этого расстояния. Формула радиального притока часто используется для определения гидропроводности по известным дебиту и давлениям.

Поскольку формулы описывают радиальную фильтрацию в пласте, то в них необходимо подставлять значение вязкости нефти при пластовых условиях, то есть при пластовых температуре и давлении с учетом соответствующего количества растворенного газа. Вычисленный дебит q (объемный расход жидкости) также получается при пластовых условиях. Для перевода дебита к нормальным поверхностным условиям необходимо вычисленный дебит разделить на объемный коэффициент пластовой жидкости.

Рассмотрим задачу притока жидкости в скважину в круговом пласте, схема которого представлена на рис. 43.

Для решения задачи введем следующие допущения:

1.Пласт круговой, в центре которого расположена единственная совершенная скважина.

2.Пласт однородный и постоянной толщины.

3.Процесс течения флюида изотермический (μ = const).

4. Движение жидкости плоско-радиальное и соответствует закону Дарси.

5.В процессе фильтрации отсутствуют любые физические и химические реакции.

Запишем уравнение Дарси:



где Q - объемный расход жидкости, м3/с;F - поверхность фильтрации, м2;

∆Р - перепад давлений, Н/м2;

μ - вязкость флюида, (Н/м2)∙с;

l -путь течения флюида, м;

k - коэффициент пропорциональности, который учитывает не только среду, в которой осуществляется фильтрация, но и все процессы взаимодействия между фильтрующимся флюидом и твердой поверхностью среды, м2.

Для схемы рис. 8.1 обозначим:

RK — радиус контура питания, м;

rс — радиус скважины, м;

h— толщина пласта, м;

Рк — давление на контуре питания, Н/м2;

Рзаб — давление на забое скважины, Н/м2.

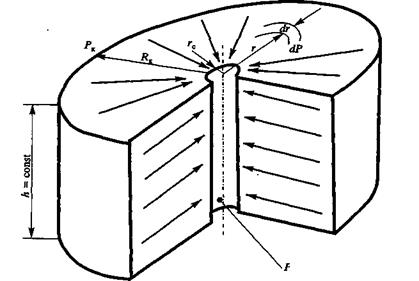Рис. 43. К выводу уравнения Дюпюи.

Выделим мысленно на расстоянии r от оси скважины элемент пласта толщиной dr. Перепад давлений на этом элементе обозначим dP. Поверхность фильтрации для выделенного элемента такова:

(1)

Запишем уравнение Дарси для рассматриваемой схемы:

после разделения переменных получим:

Пределами интегрирования для уравнения, (2) являются: по Р:отРк доРзаб;

по r: от Rк до rc.

Таким образом, имеем:

(3)

После интегрирования получим

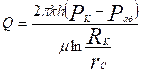(4)

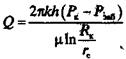Уравнение (4) называется уравнением Дюпюи и описывает приток жидкости в скважину для схемы на рис. 8.1 при принятых допущениях.

Как видно из (4), распределение давления в дяасте вокруг работающей скважины является логарифмическим, что представлено на рис. 44.



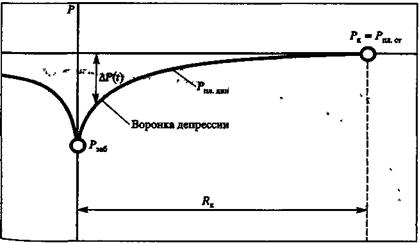
Рис 44. Распределение давления в пласте вокруг работающей скважины

Давление на контуре питания Рк является пластовым статическим давлением Рпл.ст.в дальнейшем просто Рпл (Рпл.ст - статическое пластовое давление - давление, которое существует в системе до момента отбора продукции, т.е. Когда Q =0). Давление вокруг работающей скважины в любой точке пласта (между давлением на забое скважины и давлением на контуре питания) называется динамическим пластовым давлением Рпл.дин. Динамическое пластовое давление на стенке скважины будем называть забойным давлением Рзаб. Разность между статическим и динамическим пластовыми давлениями называется депрессией АЛ:

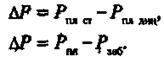(5)

Если линию распределения давления мысленно повернуть вокруг оси. скважины, получим так называемую воронку депрессии, Из рис. 8.1 видно, что депрессия (потери энергии при движении продукции от контура питания до стенки скважины) существенно возрастает на определенном расстоянии от стенки скважины.

Под призабойной зоной скважины (ПЗС) будем понимать зону, прилегающую к стенкам скважины, в которой существенно возрастают фильтрационные сопротивления движению продукции. До настоящего времени не существует никаких рекомендаций до численному определению радиуса этой зоны, что в значительной степени осложняет оценку эффективности различных методов искусственного воздействия да призабойные зоны скважин и сравнение их между собой.

Рассмотрим некоторые возможности численной оценки размеров ПЗС. Первая возможность базируется на аппроксимации ветвей логарифмической зависимости Р = f (r) прямыми линиями 1 и 2,которые пересекаются в точке А (см. рис. 45). Эта точка и дает размеры (радиус) призабойной зоны скважины — rпзс. Данный прием не является единственно возможным. Численная оценка размеров призабойной зоны может быть определена и по-другому. Например, можно разбить суммарные потери энергии при движении продукции от контура питания до стенки скважины поровну, т.е. чтобы площади S1 и S2 были равны (см. рис. 46). Граница этих площадей и будет численно определять радиус ПЗС. Совершенно очевидно, что для оценки размеров ПЗС можно предложить и другие методы.

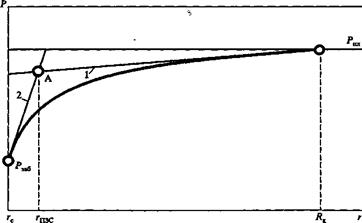Рис. 45 Первы й вариант определения радиуса ПЗС

Важно подчеркнуть: какой бы метод оценки размеров ПЗС не использовался, если возникает необходимость сравнения результатов, зависящих от размеров ПЗС, при этом сравнении необходимо в обоих случаях использовать один и тот же метод расчета размеров (радиуса) ПЗС.

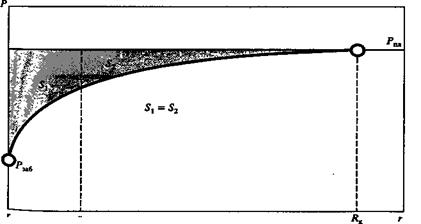Рис. 46. Второй вариант определения радиуса ПЗС

Приток жидкости и газа к скважинам

Приток нефти, газа, воды и их смесей к забоям скважин происходит при образовании на забое скважин давления меньшего, чем в продуктивном пласте. При разработке нефтяных залежей приток нефти (жидкости) и газа к скважинам происходит по радиально сходящимся к скважинам линиям.

По мере приближения жидкости и газа к скважине площади этих поверхностей непрерывно уменьшаются, а скорости фильтрации жидкости при постоянном расходе непрерывно увеличиваются, достигая максимума у стенок скважины. Таким образом, на перемещение единицы объема жидкости в направлении скважины должны непрерывно возрастать затраты энергии и связанные с этим перепады давления на единицу длины пути.

Скорость фильтрации жидкости в пористой среде, согласно закону А. Дарси (французский инженер), прямо пропорциональна перепаду давления и обратно пропорциональна вязкости жидкости:

Q- ₌ L *0.

F ц АГ

где v - скорость линейной фильтрации; Q - объемный расход жидкости через породу за 1 с; F - площадь фильтрации; к - коэффициент проницаемости породы; р - вязкость жидкости; ДР - перепад давления; Д/ - длина элемента фильтрации жидкости.

Коэффициент проницаемости из уравнения (27) будет

_{k =} QM*L

FAP ‘

На расстоянии г от центра скважины площадь фильтрации F = 2жг ■ h, а длина элемента Д/ = Дг; подставляя эти значения в формулу (27), получим

iKrRh Аг

Подставляя значения ДР = Р_пл - Р_заб и Ar = R_K-r_c, получим

С-^б=^7^1п—• »9)

2 nRh г_с

где Q - дебит скважины, м³; р - вязкость жидкости, Па с; R_K - радиус контура питания, м; R - коэффициент проницаемости пласта, м²; h - толщина продуктивного пласта, м; г_с - радиус скважины, м.

Задавая различные значения R_K и решая уравнение (29) относительно Р_пл (при условии Р_заб = const), получим изменение давления в любом направлении вокруг скважины при установившемся притоке в виде логарифмической кривой (рис. 25), называемой воронкой депрессии.

Как видно из рис. 25, основной перепад давления в пласте происходит в непосредственной близости от скважины. По мере удаления от нее кривая распределения давления выполаживается, что говорит о значительном уменьшении скоростей фильтрации с удалением от скважины. Записав уравнение относительно Q,

получим уравнение Ж. Дюпюи для радиально установившегося притока однородной жидкости в скважину:

q _ -^заб)

м^К/^гс

Данное уравнение применимо для так называемой гидродинамически совершенной скважины.

За гидродинамически совершенную скважину в нефтепромысловой практике принимают скважину с открытым забоем, где фильтрационные потоки движутся к скважине параллельно друг другу, кровле и подошве пласта (рис. 26 а).

а) в)




////////////Л \ у//////////} У//////////Л

Рис. 26. Виды гидродинамического несовершенства скважин

Скважины чаще всего гидродинамически несовершенны. Гидродинамическое несовершенство скважин проявляется появлением дополнительных сопротивлений, возникающих в призабойной зоне у стенок скважины вследствие отклонения потока жидкости от плоскопараллельного, а также в результате сгущения линий токов у перфорационных отверстий, вызывающих местное повышение скоростей движения жидкости.

Бывают гидродинамически несовершенные скважины по степени вскрытия, где продуктивные пласты вскрывают не на всю толщину (рис. 26 б). Линии тока к этим скважинам от кровли

до забоя параллельны, а ниже уровня забоя искривляются, в результате чего возникают дополнительные гидравлические сопротивления. По характеру вскрытия большая часть скважин является гидродинамически несовершенной. При этом вскрывается продуктивный пласт на всю его толщину, но сообщение с ним происходит через перфорационные отверстия в эксплуатационной колонне (рис. 26 в).

Встречаются также скважины несовершенные и по степени, и по характеру вскрытия (рис. 26 г).

Уравнение движения жидкости в несовершенную скважину описывается следующей формулой:

2жШ(Р_пп-Р_заб)

^Q* //(InRjr_c+c) ’ ⁽

где Q_H - дебит жидкости гидродинамически несовершенной скважины и по характеру, и по степени вскрытия.

Отношение дебита жидкости гидродинамически несовершенной скважины к дебиту жидкости гидродинамически совершенной при равных условиях называется коэффициентом гидродинамического несовершенства скважины, который всегда меньше единицы, то есть выражается в долях от 1:

Q_H _ In Rjr_c Q In R_K/r_c+c’

где Q - дебит гидродинамически совершенной скважины.

Но коэффициент с трудно определить, так как неизвестно, сколько отверстий образовалось в результате перфорации, какова глубина и диаметр этих отверстий. Поэтому вместо гидродинамически несовершенной скважины принимается гидродинамически совершенная скважина с меньшим радиусом. Радиус этой условной скважины называется приведенным, а дебит ее

q _ 2xRh(P_nn- Р_заб)

М^К/г_пр

где г_лр - приведенный радиус скважины, который определяется

расчетным путем по данным гидродинамических исследований скважин.

Как уже отмечалось, на жидкость, газ и воду в пласте действует пластовое давление.

Пластовое давление - это давление, замеренное в остановленной (закрытой) скважине. Уровень жидкости в скважине, установившийся при этом, называется статическим уровнем. Расстояние до уровня в скважине измеряется от устья, а высота столба жидкости - от забоя до статического уровня:

H„=H-h, (34)

где Я_ст - статический уровень в скважине, м; Н - глубина скважины, м; h - расстояние от устья до уровня в скважине, м.

В случае когда пластовое давление превышает давление столба жидкости в заполненной скважине, при открытом устье жидкость будет переливаться из скважины.

В работающей скважине давление на забое (забойное давление) устанавливается ниже пластового, и в затрубном пространстве скважины устанавливается другой уровень жидкости, который называется динамическим уровнем. Динамический уровень всегда меньше статического.

Объем нефти, поступающей к забою скважины, зависит от коллекторских свойств пласта, вязкости нефти и перепада давления, то есть разницы между пластовым и забойным давлением. Наибольшая зависимость наблюдается между дебитом (количеством) поступающей жидкости к забою скважины и перепадом давления.

Уравнение притока нефти (жидкости) к скважине при этом записывается как

Я = К(Р_ПЛ-Р_г) = КАР, (35)

где Q - дебит нефти (жидкости), т/сут; К - коэффициент продуктивности, равный приросту дебита скважины в сутки на единицу снижения забойного давления при постоянном пластовом давлении (Р_пл = const); Р_пл - пластовое давление, МПа; Д - забойное давление, МПа.

Когда известны коэффициент продуктивности и пластовое давление, определяется дебит скважины при определенном снижении забойного давления.

На практике коэффициент продуктивности определяют по данным исследовательских работ в скважине. На определен-

ном режиме работы скважины замеряют дебит нефти (жидкости) и одновременно замеряется забойное давление. После этого меняют режим работы скважины и вновь замеряют дебит и забойное давление. По результатам определяется зависимость дебита скважины от забойного давления. Зная дебиты жидкости и соответствующие им перепады давления (депрессии), строят кривую зависимости притока жидкости от перепада давлений, которая называется индикаторной линией. Строят график, на котором по вертикальной оси откладывают значения перепадов давлений, а по горизонтальной оси откладывают значения дебитов жидкости. На графике каждому значению перепада давления соответствует определенный дебит жидкости.

Индикаторные линии могут быть прямыми и выпуклыми и вогнутыми относительно оси дебитов (кривые рис. 27).

Выпуклые индикаторные кривые бывают, когда вместе с нефтью извлекается газ или при больших перепадах давления.

Теоретически, при соблюдении закона Дарси, максимальная производительность скважины может быть при Р_иб = 0, и эту производительность называют потенциальным дебитом:

Фпот ^{— iw} ПЛ •

Но практически потенциального дебита получить невозможно, так как в скважине сохраняется какой-то столб жидкости. При исследовании скважин дебиты нефти замеряют на поверхности в ГЗУ (групповые замерные установки) за соответствующую единицу времени, пересчитываемую на дебит жидкости скважины в м³ или тоннах в сутки. Дебиты газа замеряются газовыми счетчиками-расходомерами. Пластовые давления замеряются с помощью глубинных манометров, спускаемых в скважины на стальной проволоке.

2. Графическая информация в тексте

Любая графическая информация в тексте (чертежи, графики, схемы, компьютерные распечатки, диаграммы, фотоснимкам, прочее) считается иллюстрацией. Ссылки на иллюстрации и подписи к иллюстрациям оформляются так, как указано в данном предложении и на приведенной иллюстрации (рис. 1). Обратите внимание – красная строка (отступ) в формате отсутствует как у иллюстрации, так и у ее названия. Выравниваются по центру, точка в конце названия иллюстрации не ставится. Нумерация иллюстраций – арабскими цифрами, сквозная по всем разделам.



Рисунок 1 - Это иллюстрация (название)
Раздел не может содержать только иллюстрации без пояснительного текста.

Не соблюдение требований к оформлению повлечет только ухудшение оценки реферата.
3. Табличная информация в тексте

Ссылки на таблицы и названия таблиц оформляются так, как указано в данном предложении и в приведенной таблице (табл. 1). Обратите внимание – у названия таблицы красная строка (отступ) в формате отсутствует. Название выравнивается по левому краю, точка в конце названия таблицы не ставится. Границы таблиц не должны выходить за границы текста. При большой ширине таблиц допускается разворачивать их вместе с номером и названием на 90º против часовой стрелки. Если таблица не помещается на странице, то таблица переносится на следующую с дублированием заголовка таблицы или строки с нумерацией столбцов и размещением над правым верхним углом надписи в полужирном начертании: продолжение таблицы ХХХ.

Нумерация таблиц – сквозная по всему тексту.

Таблица 1 - Это пример таблицы (название)

№ пп	Параметр 1	Параметр 2	Параметр 3
1	2	3	4
1	ХХХ	ХХХ	ХХХ
2	ХХХ	ХХХ	ХХХ
3	ХХХ	ХХХ	ХХХ

Раздел не может содержать только таблицы без пояснительного текста.

Не соблюдение требований к оформлению повлечет только ухудшение оценки реферата.
Заключение

Подводит итог работы. Оно может содержать повторение основных тезисов работы, общий вывод, к которому подошел автор, может содержать предложение по дальнейшему изучению проблемы.

Здесь уже никакие конкретные случаи, цифры не анализируются. «Заключение» по объему всегда меньше «Введения». Считается, что объем «Заключения» составляет 1/20 часть работы.
Список использованных источников

1. ГОСТ 7.32-2017 Система стандартов по информации, библиотечному и издательскому делу. Отчет о научно-исследовательской работе. Структура и правила оформления. - М.:Стандартинформ, 2017. - 24 с.