Реферат. Реферат по теме многоугольники на решетках. Формула пика.

• Название: Реферат по теме многоугольники на решетках. Формула пика.
• Анкор: Реферат.docx
• Дата: 05.04.2018
• Размер: 116.83 Kb.
• Имя файла: Реферат.docx
• Тип: Реферат; #17639

РЕФЕРАТ

ПО ТЕМЕ «МНОГОУГОЛЬНИКИ НА РЕШЕТКАХ. ФОРМУЛА ПИКА.»

Подготовила ученица 9 «Б»

Баранова Александра
Введение
Клетчатая бумага (точнее — ее узлы), на которой мы часто предпочитаем рисовать и чертить, является одним из важнейших примеров точечной решетки на плоскости. Уже эта простая решетка послужила К. Гауссу отправной точкой для сравнения площади круга с числом точек с целыми координатами, находящихся внутри него. То, что некоторые простые геометрические утверждения о фигурах на плоскости имеют глубокие следствия в арифметических исследованиях, было в явном виде замечено Г. Минковским в 1896 г., когда он впервые для рассмотрения теоретико-числовых проблем привлек геометрические методы.
Решетка на плоскости является мощным средством, которое позволяет переводить аналитические задачи на геометрический язык и обратно. Движение на этом своеобразном мосту между анализом и геометрией стало достаточно интенсивным и двусторонним.
Решетки на плоскости и в пространстве
Рассмотрим на плоскости два семейства параллельных прямых, разбивающих плоскость на равные параллелограммы; множество L всех точек пересечения этих прямых (или множество вершин всех параллелограммов) называется точечной решеткой или просто решеткой, а сами точки — узлами решетки. Любой из этих параллелограммов называется фундаментальным параллелограммом или параллелограммом, порождающим решетку.

Задать решетку можно еще и так. Предположим, что на плоскости

заданы две пересекающиеся прямые l0 и m0, а также два положительных числа a и b. По обе стороны от прямой l0 проведем параллельные прямые l±1, l±2, l±3,… на расстояниях a, 2a, 3a,… от нее. Аналогично по обе стороны от прямой m0 на расстояниях b, 2b, 3b,… проведем прямые m±1, m±2, m±3,…

Отметим все точки пересечения прямых l_i c прямыми m_j; множество всех этих точек пересечения и является решеткой L

Важно иметь в виду, что решетка состоит из точек (узлов), а сами

прямые к ней не относятся. Одна и та же решетка может быть получена

при помощи различных семейств параллельных прямых.

Отметим ряд простейших свойств произвольных точечных решеток.

1. Прямая, проходящая через два узла решетки, содержит бесконечно много узлов решетки. При этом все расстояния между соседними узлами, лежащими на этой прямой, равны между собой.

2. Преобразование параллельного переноса плоскости (пространства), переводящего один узел решетки в другой ее узел, переводит решетку саму в себя.

3. Решетка центрально-симметрична относительно середины любого отрезка, который соединяет два узла этой решетки. Более того, середины всех отрезков с концами в узлах данной решетки образуют новую решетку, включающую старую.

4. (Правило параллелограмма.) Если три вершины параллелограмма являются узлами решетки, то и четвертая его вершина — тоже узел решетки. В пространстве: если четыре вершины параллелепипеда, не лежащие в одной плоскости, являются узлами решетки, то и остальные его вершины — также узлы решетки.

5. Если параллелограмм с вершинами в узлах решетки не содержит других узлов на сторонах и внутри себя, то он эту решетку порождает, т.е. является ее фундаментальным параллелограммом. Более того, это свойство является критерием того, что параллелограмм является фундаментальным.

На рисунке изображена так называемая ортогональная целочисленная решетка Z², состоящая из точек с целыми координатами в декартовой системе координат. То же семейство точек можно получить пересечением других семейств прямых, не являющихся ортогональными. Таким образом, решетка точек напрямую не связана с семейством прямых в отличие от ее фундаментального параллелограмма.
Правильные многоугольники на решетках

Треугольник и квадрат.

Теорема 1:

Правильный треугольник нельзя расположить на целочисленной решетке Z².

Доказательство:

Предположим, что какой-либо правильный треугольник можно расположить на решетке нужным образом и что начало координат находится в одной из его вершин, а две другие его вершины имеют координаты (a, b) и (c, d). Можно считать, что четыре целых числа a, b, c, d не имеют общих делителей, отличных от ±1. Последнее следует из того, что точки (0, 0), (a/k, b/k), (c/k, d/k) также являются вершинами правильного треугольника, если k — общий делитель всех четырех чисел.

Так как a²+b²=c²+d²=(a−c)²+(b−d) ², то отсюда заключаем, что a²+b²=c²+d²= 2(ac+bd).
Следовательно, a²+b²+c²+d²= 4(ac+bd), т.е. сумма квадратов четырех чисел делится на 4. Но тогда или все четыре числа четные, или все нечетные. Первое невозможно потому, что эти числа, по нашему выбору, взаимно просты. Второе же невозможно потому, что тогда не выполняется соотношение a²+b²= (a−c)²+ (b−d)², ибо его левая часть не делится на 4, а правая — делится. Полученное противоречие и доказывает сформулированное утверждение.

Существует еще много самых разнообразных доказательств для правильного треугольника.

Ясно, что правильный шестиугольник также нельзя расположить

на решетке Z², так как в противном случае, соединив его вершины через одну, мы получили бы правильный треугольник, расположенный на решетке, что, как мы уже знаем, невозможно. Однако в пространстве на решетке Z³ можно расположить как правильный треугольник, так и правильный шестиугольник. Достаточно предъявить правильный шестиугольник.
Теорема 2:

Не существует плоской решетки, содержащей одновременно квадрат и правильный треугольник.

Доказательство:

Предположим противное, т.е. что на некоторой решетке L можно одновременно расположить правильный треугольник T=ABC и квадрат K=APQR.

Начиная с квадрата K, построим решетку L0. Так как tg 60^◦=√3 иррациональное число, то один из лучей [AB) или [AC) не содержит ни одного узла решетки L0, отличного от A; пусть это будет луч [AC). На этом луче находится бесконечно много узлов C1,C2,C3,... решетки L и, более того, тангенс угла наклона этого луча с любой прямой, параллельной стороне PQ квадрата K, является числом иррациональным. Обозначим через Dk «левую нижнюю» вершину квадрата решетки L0, в который попала точка Ck. Для каждого k≥1 рассмотрим параллелограмм ACk Dk Ek. По правилу параллелограмма, все полученные таким образом точки Ek, являются узлами решетки L и расположены внутри квадрата APQR. Кроме того, все точки Ek различны, так как если Ek=Ek+m, то прямая Dk Dk+m параллельна прямой AC и проходит через узлы решетки L0. Поэтому тангенс угла наклона прямой Dk Dk+m с прямыми, параллельными стороне PQ квадрата K, является рациональным числом, что невозможно.

Итак, внутри квадрата K находится бесконечно много различных точек решетки L, что означает, что найдутся два ее узла, которые находятся на произвольно малом расстоянии друг от друга. На решетках это невозможно и полученное противоречие доказывает теорему.

Правильные многоугольники

Правильный пятиугольник, так же как и правильный треугольник, нельзя поместить ни на целочисленную решетку Z² в плоскости, ни на решетку Z3 в пространстве. Не существует ни одной решетки L (двух или более измерений), куда можно было бы поместить правильный пятиугольник.

Единственным правильным многоугольником на плоскости, все координаты вершин которого рациональны, является квадрат.

Полуправильные многоугольники

Рассмотрим множество равноугольных (равносторонних) многоугольников—таких, у которых все внутренние углы (все стороны) равны, но стороны (внутренние углы) могут и отличаться друг от друга; пересечение этих множеств составляет множество правильных многоугольников. Примерами равноугольных многоугольников, расположенных на решетке, служат квадрат и восьмиугольник.

Из всех возможных равноугольных многоугольников на решетке Z2 можно расположить только прямоугольник и восьмиугольник.
Формула Пика

Пусть — число целочисленных точек внутри многоугольника, — количество целочисленных точек на его границе, — его площадь. Тогда справедлива формула Пика:



Доказательство: Рассмотрим прямоугольник со сторонами, лежащими на линиях решетки. Пусть длины его сторон равны и . Имеем в этом случае

и, по формуле Пика,



Рассмотрим теперь прямоугольный треугольник с катетами, лежащими на осях координат. Такой треугольник получается из прямоугольника со сторонами и , рассмотренного в предыдущем случае, разрезанием его по диагонали. Пусть на диагонали лежат целочисленных точек. Тогда для этого случая

и получаем, что



Теперь рассмотрим произвольный треугольник. Его можно получить, отрезав от прямоугольника несколько прямоугольных треугольников и, возможно, прямоугольник. Поскольку и для прямоугольника, и для прямоугольного треугольника формула Пика верна, мы получаем, что она будет справедлива и для произвольного треугольника.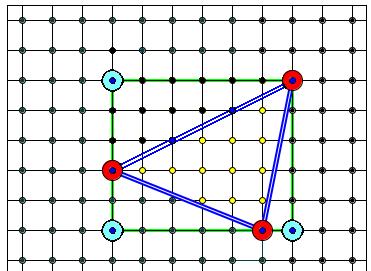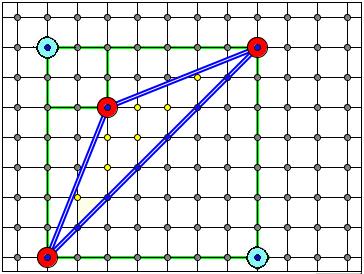



Остается сделать последний шаг: перейти от треугольников к многоугольникам. Любой многоугольник можно разбить на треугольники (например, диагоналями). Поэтому нужно просто доказать, что при добавлении любого треугольника к произвольному многоугольнику формула Пика остается верной.

Пусть многоугольник и треугольник имеют общую сторону. Предположим, что для формула Пика справедлива, докажем, что она будет верна и для многоугольника, полученного из добавлением . Так как и имеют общую сторону, то все целочисленные точки, лежащие на этой стороне, кроме двух вершин, становятся внутренними точками нового многоугольника. Вершины же будут граничными точками. Обозначим число общих точек через и получим

— число внутренних целочисленных точек нового многоугольника,

— число граничных точек нового многоугольника.

Из этих равенств получаем



Так как мы предположили, что теорема верна для и для по отдельности, то









Тем самым, формула Пика доказана.