Реферат. Реферат по теме Применение формулы Кобба Дугласа в решении производственных задач

• Название: Реферат по теме Применение формулы Кобба Дугласа в решении производственных задач
• Анкор: Реферат
• Дата: 08.06.2022
• Размер: 50.96 Kb.
• Имя файла: Реферат.docx
• Тип: Реферат; #577254

Реферат по теме:
«Применение формулы Кобба Дугласа в решении производственных задач»


Определение производственных функций

Под производством понимается процесс взаимодействия экономических факторов, завершаемый выпуском какой-либо продукции. Правила, предписывающие определенный порядок взаимодействия экономических факторов, составляют способ производства или, иначе говоря, технологию производства. Производство - основная область деятельности фирмы (или предприятия). Фирма - это организация, производящая затраты экономических ресурсов для изготовления продукции и услуг, которые она продает потребителям, в том числе, другим фирмам. Производственными единицами являются не только заводы и фабрики, но и отдельные лица - фермеры, ремесленники и др.

Производство можно представить как систему "затраты-выпуск", в которой выпуском является то, что фактически произведено, а затратами - то, что потребляется с целью выпуска (капитал, труд, энергия, сырье). Поэтому формально можно сказать, что производство - это функция, которая каждому набору затрат и конкретной технологии ставит в соответствие определенный выпуск. Именно такое упрощенное понимание производства как "черного ящика" заложено в математической модели производства. Во "вход" этого черного ящика подаются затраты, а на "выходе" получаем выпуск (произведенную продукцию).

Конечной целью фирмы является получение наибольшей прибыли от реализации своей продукции. Напомним в этой связи, что прибыль понимается как разность двух величин: выручки от реализации продукции (дохода) и издержек производства. Издержки производства равны общим выплатам за все виды затрат, иначе говоря, издержки - это денежный эквивалент материальных затрат. В общем случае издержки состоят из двух слагаемых: постоянных издержек и переменных издержек. Постоянные издержки (расходы на закупку и ремонт оборудования, содержание фирмы, страховку и пр.) фирма несет независимо от объема выпуска. Переменные издержки (расходы на заработную плату, сырье и пр.) касаются использования уже имеющихся в распоряжении фирмы ресурсов, производственных мощностей и меняются вместе с объемом выпуска.

Перед тем, как построить ту или иную оптимизационную модель задачи фирмы, более подробно остановимся на способах формализации этих понятий и рассмотрим некоторые их свойства. Предположим, что фирма производит nвидов продуктов. Виды продуктов будем обозначать индексом j, а их количества - через y_j, j 1,...,n^{. Технология производства каждого вида продукта требует} использования ряда ресурсов в некоторых количествах. Двойными индексами k_j обозначим виды ресурсов, используемых для выпуска продукта вида j. Пусть k1, 2,..., m_j. Обозначим через x
j

k
j количества этих ресурсов, k_j1, 2,..., m_j, j1,...,n. Следовательно, имеется всего m₁ ... m_n видов ресурсов. Использование такой двойной индексации привлекательно с точки зрения информативности (видно, какой ресурс относится к какому продукту), но неудобно чисто технически. Во-первых, усложняется запись формул; во- вторых, увеличивается размерность задачи (т.к. среди m₁, m₂,.., m_n могут быть одни и те же наименования) и, в-третьих, такие операции как сложение, вычитание затрат в векторной форме, а также составление уравнений становятся невозможными без дополнительных преобразований индексов (идентификация, упорядочение и т.д.). Поэтому в дальнейшем виды ресурсов будем обозначать одинарными индексами k, их количества - x_k, где k1,...,m^{. Здесь m- достаточно} большое число (равное сумме m₁ ... m_n, где каждый ресурс считается только один раз). Теперь можно говорить, что для производства n видов продуктов фирма использует m видов затрат. Это не приводит к недоразумениям, так как в случае неиспользования ^k-го ресурса для выпуска данного продукта полагаем x_k 0 ^. Введем в рассмотрение два вида векторов: x _x₁,..., x_m вектор затрат и y _ y₁,..., y_n вектор выпуска. Положительный ортант

R^m _x R^m/ x_k 0, k1,..., m_ называется пространством затрат.

Аналогично определяется пространство выпуска:

Rⁿ _x Rⁿ/ y_j

 0, ^{j1,..., n}_.

Для отражения реальных возможностей фирмы в математических моделях часто применяются более узкие множества X R^{m и} Y R^n.








Технологическая связь между затратами и выпуском описывается с помощью производственной функции Это есть определение производственной функции для многопродуктовой фирмы, т.е. векторной производственной функции. Если фирма выпускает только один вид продукта, то производственная функция является скалярной:
 
f: R^m R¹ или y f_x₁, x₂,..., x_n В общем случае производственную функцию можно записать в неявной форме: ^F_^{x, y, A}_ ^{ 0} , где A- nm матрица параметров (технологическая матрица). В некоторых моделях применяется следующее выражение для производственной функции:

^F_^z₁^{,..., zr, A}_ ^{ 0} , где переменные выпуски. z_iсо знаком "-" - обозначают затраты, а со знаком "+" - Если в качестве независимых переменных (аргументов) выступают затраты, то производственную функцию иногда называют функцией выпуска, если же фиксирована величина выпуска ( y), то производственная функция является функцией затрат ( x f^1_ y_). Таким образом, функция выпуска и функция затрат являются взаимно обратными друг другу функциями. Производственная функция Кобба-Дугласа. Первый успешный опыт построения производственной функции, как уравнения регрессии на базе статистических данных, был получен американскими учеными - математиком Д. Коббом и экономистом П. Дугласом в 1928 году.


1 2
Предложенная ими функция изначально имела вид: Y a K^  L^1 _ f_x₁, x_{2 }  a x^  x^1 _, где Y- объем выпуска, K- величина производственных фондов (капитал), L затраты труда, a 0,   0 числовые параметры (масштабное число и показатель эластичности). Благодаря своей простоте и рациональности, эта функция широко применяется до сих пор и получила дальнейшие обобщения в различных направлениях. Функцию Кобба-Дугласа иногда мы будем записывать в виде
1 2
f_x₁, x_{2 }  a x^1  x^2 , ₁ ₂ 1. Легко проверить, что Y_0,0_  0 _и YK  0 , ^Y 0 ,L ²YK²  0 , ²YL²  0 . Кроме того, функция линейно-однородна: Y_K,L_  a_K_^ _L_1^  aK^ L^1  Y_K,L_.Таким образом, функция Кобба-Дугласа обладает всеми вышеуказанными свойствами. Для многофакторного производства функция Кобба-Дугласа имеет вид: ^f ^x ^{ a x1  x2 ... xm, } ..._m1. 1 2 ^m1 Для учета технического прогресса в функцию Кобба-Дугласа вводят специальный множитель (технического прогресса) ^et, где t- параметр времени,  - постоянное число, характеризующее темп развития. В результате функция принимает "динамический" вид: ^f ^x ^{ ae tx x .} Для конкретных наименований ресурсов средние и предельные величины приобретают смысл конкретных экономических показателей. Рассмотрим, например, функцию Кобба-Дугласа , где x₁  K- капитал, а x L- труд. Средние продукты ^{f C Y}  aK^ L^ , 2 ^L_L f^C ^Y _{ aK} 1_L1 имеют смысл соответственно средней _K производительности труда и средней производительности капитала (средней фондоотдачи). Видно, что средняя производительность труда убывает с ростом трудовых ресурсов. Это и понятно, так как производственные фонды ( K) остаются неизменными, и потому вновь привлекаемая рабочая сила не обеспечивается дополнительными средствами производства, что и приводит к снижению производительности труда. Аналогичное рассуждение верно и для фондоотдачи как функции от капитала. Для функции предельные продукты _fП Y  a_1 _ K^ L^  _1 a_ f^C, _fП Y _{ a K} 1_L1   f^C L ^LK_K^K имеют смысл соответственно предельной производительности труда и предельной производительности капитала (предельной фондоотдачи). В микроэкономической теории производства считается, что предельная производительность труда  ^Y
L
   равна заработной плате (цене труда), а предельная производительность капитала  ^Y
K
   рентным платежам (цене услуг капитальных благ). Из условия следует, что при неизменных основных фондах (трудовых затратах) увеличение численности работающих (объема основных фондов) приводит к падению предельной производительности труда (предельной фондоотдачи). Видно, что для функции Кобба-Дугласа предельные продукты пропорциональны средним продуктам и меньше их. Неоклассическая производственная функция и ее частный вид – функция Кобба-Дугласа.

Все те применения производственных функций, будут иметь место на практике экономических исследований и приносить реальную пользу только в том случае, если они как модели взаимосвязи "затраты-выпуск" будут адекватно отражать действительность. Поэтому важная задача теории - разработка достоверных и реалистических методов построения производственных функций. По существу, производственная функция fесть совокупность "правил", с помощью которых для каждого набора затрат _x₁,..., x_mопределяется соответствующий выпуск y: y f_x₁,..., x_m^{. Поэтому} построение производственной функции означает нахождение математической формулы, отражающей эти правила или, иначе говоря, закономерности превращения набора ресурсов в конечный продукт. Этот процесс условно можно представить схемой: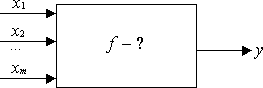



Схема превращения ресурсов в конечный продукт

В блоке f ,образно говоря, происходит "смешивание" ресурсов x₁,..., x_m в определенных "пропорциях" таким образом, чтобы получился требуемый продукт. Эти "пропорции" определяются спецификой производства и математически выражаются с помощью различных коэффициентов и показателей степени для величин x₁,..., x_m. "Смешивание" их математически выражается с помощью разных формальных операций между ними (суммирования, произведения, логарифмирования и т.д.), вид и сочетание которых также определяется спецификой моделируемого производства. Так что вопрос построения производственной функции в каждом конкретном случае сводится к нахождению этих "пропорций" и к определению характера их "смешивания".

Из сказанного выше следует, что для построения производственных функций нужно знать технологию производства, ее структуру и организацию, а также принципы работы сложных машин и оборудования, т.е. надо быть одновременно и технологом, и инженером, и математиком. Оказывается, что знание всего этого сложного производственного механизма не требуется, если владеть подходящими математическими приемами. Речь идет об использовании методов регрессионного анализа на основе статистических (опытных, экспертных) данных о затратах и выпуске. Не умаляя достоинства других математических и иных методов построения производственных функций, можно сказать, что именно методы регрессионного анализа наилучшим образом оправдали себя на практике и потому являются наиболее популярными. Идею применения статистических данных для построения производственной функции можно объяснить на рисунке. Имеются известные величины x₁,..., x_m, y(реальные результаты производства) и одно неизвестное выражение f , их связующее. Наблюдая в течение достаточно большого периода времени функционирования производства за различными значениями затрат x₁,..., x_m и соответствующими им значениями выпуска y, можно выявить закономерность. Например, свою знаменитую функциюКобб и Дуглас получили на основе изучения статистических данных по расходованию капитала ( K), труда ( L) и индекса производства (Y) в американской обрабатывающей промышленности за период с 1899 по 1922 гг. Практическая значимость этой функции подтверждается тем, что соответствующая замена исходных данных позволяет использовать ее для анализа любого производства.

Кратко остановимся на этапах построения производственной функции. Пусть нам известны виды ресурсов ( i1,...,m), используемых для выпуска данной продукции, и имеется необходимое количество статистических данных по объемам затрат x₁,..., x_m и выпуска y. Требуется установить зависимость y f_x₁,..., x_m^{, т.е. найти аналитический вид} производственной функции f. Эта задача распадается на два этапа: спецификация функции f, т.е. выявление общего вида функции fот аргументов x₁,..., x_m с неопределенными параметрами ^{(коэффициентами и показателями степеней при} x_iчленом); и свободным

1. 
   оценка параметров - определение конкретных числовых значений неизвестных параметров.
   

Картина "расположения" статистических данных в пространстве затраты-выпуск может подсказать линейный или нелинейный характер

зависимости функции fот аргументов x₁,..., x_m. Например, в случае линейной производственной функции результатом спецификации будет гипотеза о линейной зависимости вида ^f ^x ^{ }₁^x₁ ^₂^x₂ ^..._m^x_m^, в случае производственной функции Кобба-Дугласа - в виде мультипликативной функции mf_ x_  b _ bx^k, k1 ^kв случае производственной функции CES - в виде степенного многочлена

^f ^x ^{ c} l
m
_ cx^{r } k1 ^{kk }и т.д. Здесь  a,a_k ,b,b_k,c,c_k,r,lявляются неизвестными параметрами, подлежащими определению. ^a_x_^1 _x _^2 ^ _{1 2}  _ _ f_ x_  lim ^    ^^{ 1} 

_a_ x_ ¹ _ x_ ² 1 2 ^a^12  x^1  x^{2 } lim ^{12}  ^
1 2
1 _ a^12  x^1  x^{2    1  } ^ lim ^a_₁ _{2 } ^{1 2}  x₁ ¹  x₂ ²    1   ^{ }1^ a ^{1 2}  x₁ ¹  x₂ ^{2 } 
1
 lim _₁ _{2 } _₁ _{2 }

Изокванты, предельная производительность и предельная норма замещения ресурсов

Рассмотрим геометрическую иллюстрацию оптимального решения задачи в пространстве затрат. Для этого Изокванты введем два геометрических понятия - изокванты и изокосты. в теории производства играют такую же роль, что и кривые безразличия в теории потребления. Определение Изоквантой (производственной функции f : R^m R¹) называется геометрическое место всех векторов затрат x, использование которых приводит к одному и тому же объему выпуска продукции y⁰ :_ xR^m/ f_x_  y⁰_. Таким образом, изокванта - это линия уровня производственной функции. Для различных уровней выпуска y⁰ линии уровня f_ x_  y^{0 заполняют все пространство затрат (} R^{m) и составляют карту изоквант. Для} примера на рисунке приведен вид изоквант производственной функции Кобба-Дугласа.   x^  x^1  y⁰ _y⁰  const_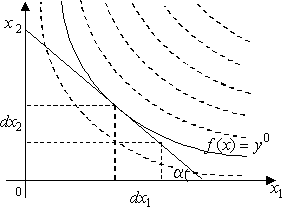
Изокванта