пример кур. Реферат пояснительная записка с., рис., табл., приложений, источников
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
6.7.1 Разработка детерминированной математической моделиФизико-математические модели агломерационного процесса могут быть получены аналитически, путем последовательного описания физических и химических превращений в исходных материалах в процессе производства [21]. Динамическая математическая модель спекания агломерационной шихты, реализуемая на ЭВМ, позволяет быстро и с минимальными затратами исследовать влияние ведущих параметров процесса спекания (высоты слоя шихты, содержания углерода и влаги в шихте, скорости движения спекательных тележек и др.) на его технико-экономические показатели и может быть использована в качестве информационной части в АСУ агломерационным производством для оптимизации технологического процесса. Алгоритм динамического моделирования в математической форме отражает физико-химические превращения и тепловые явления в спекаемом слое шихты практически в той мере, в какой процесс агломерации в настоящее время может быть описан аналитически. В алгоритм динамической модели процесса спекания включены зажигание, сушка (переувлажнение) шихты, горение топлива, нагрев и охлаждение слоя шихты, изменение расхода газов, плотности шихты, теплоемкости материалов и газов, коэффициентов тепло- и влагообмена по ходу технологического процесса. Некоторые химические (в том числе минералогические) превращения в настоящее время исследованы и описаны недостаточно полно, поэтому их влияние на процесс можно учесть только приблизительно, путем некоторой коррекции теплофизических свойств шихты и агломерата, материального баланса и других хорошо изученных факторов. Математическая модель основана на следующих предпосылках. Ввиду малых размеров частиц шихты их температура постоянна по объему; все частицы элементарного объема шихты, расположенные на одном горизонте слоя, имеют одинаковую температуру; тепловые эффекты реакций локализованы в объеме частиц шихты; теплообмен между шихтой и газовым потоком происходит при граничных условиях третьего рода; теплообмен теплопроводностью или излучением между слоями шихты, расположенными на различных горизонтах, отсутствует; теплота плавления и кристаллизации выражена зависимостью теплоемкости материалов от температуры; теплоемкости шихты и агломерата одинаковы; теплота экзо- и эндотермических реакций, а также потери теплоты с механическим недожогом и в окружающую среду определяются путем коррекции тепловыделения при горении коксика (по тепловому балансу); кислород диссоциирующих оксидов рассчитывается по уравнению, в котором содержание кислорода в воздухе корректируют с помощью коэффициентов (по материальному балансу); аккумуляцией теплоты и массы газами в слое можно пренебречь, так как она мала по сравнению с аккумуляцией теплоты и массы материалами; теплоемкость газов не зависит от их состава. Многие из этих допущений не влияют сколько-нибудь существенно на структуру алгоритма моделирования. В слое спекаемой агломерационной шихты протекают процессы горения топлива, тепло- и влагообмена; изменяются давления водяных паров в газах, насыпная плотность шихты, теплоемкость шихтовых материалов, агломерата и продуктов сгорания. Некоторые из этих физических и химических явлений математически могут быть охарактеризованы системой алгебраических уравнений, не содержащих пространственной координаты и времени. Действительно, зависимости коэффициента теплоотдачи от температуры и состава шихты или теплоемкости газов от температуры сохраняются в любом месте слоя в любой момент времени. Это же относится и к другим подобным зависимостям. Рассмотрим алгебраические уравнения модели. При горении топлива выделяется теплота: 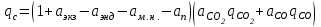 , (6.7.1) , (6.7.1)где 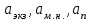 - тепловые эффекты экзо- и эндотермических реакций, потери с механическим недожогом и в окружающую среду, выраженные в долях от теплоты сгорания; - тепловые эффекты экзо- и эндотермических реакций, потери с механическим недожогом и в окружающую среду, выраженные в долях от теплоты сгорания; 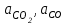 - доля углерода, сгорающего до СО2 и СО; - доля углерода, сгорающего до СО2 и СО; 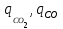 - теплоты сгорания углерода до СО2 и СО. - теплоты сгорания углерода до СО2 и СО.Совместное протекание тепло- и влагообмена в слое характеризуется психрометрическим коэффициентом: 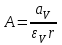 , (6.7.2) , (6.7.2)Здесь 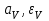 - объемные коэффициенты теплоотдачи и влагообмена; - объемные коэффициенты теплоотдачи и влагообмена; r — теплота парообразования. Коэффициент теплоотдачи между газами и шихтой зависит от скорости и температуры газов и уменьшается в процессе сушки и спекания шихты, поэтому можно записать: 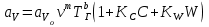 , (6.7.3) , (6.7.3)где v - скорость продуктов сгорания в свободном сечении слоя; ТГ - абсолютная температура газа; С - содержание углерода в шихте; W - влажность шихты; 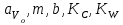 - постоянные. - постоянные. Давление насыщенных водяных паров в продуктах сгорания Рнас зависит от температуры шихты tш и величины нормального давления Рн: 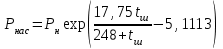 (6.7.4) (6.7.4)Парциальное давление водяных паров в газах Рв.п. можно выразить через парциальную скорость 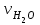 и абсолютное давление продуктов сгорания Р: и абсолютное давление продуктов сгорания Р:Рв.п = Р 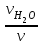 (6.7.5) (6.7.5)Насыпная плотность шихты 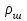 зависит от ее абсолютной плотности зависит от ее абсолютной плотности 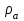 и пористости П: и пористости П: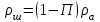 (6.7.6) (6.7.6)Если допустимо некоторое уменьшение точности моделирования, то можно принять 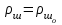 = const. Для расчетов повышенной точности может быть использована величина усадки шихты, зависящая от разрежения в вакуум-камерах, высоты слоя и других факторов. На теплоемкость шихтовых материалов Сш и газов С влияет температура шихты tш и газов tг: = const. Для расчетов повышенной точности может быть использована величина усадки шихты, зависящая от разрежения в вакуум-камерах, высоты слоя и других факторов. На теплоемкость шихтовых материалов Сш и газов С влияет температура шихты tш и газов tг: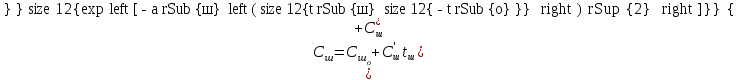 (6.7.7) (6.7.7)С = Сг.о + C'г fг, (6.7.8) где 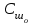 , ,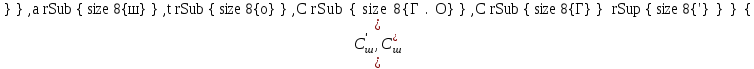 - постоянные. - постоянные.Продукты сгорания, проходящие через спекаемый слой, состоят из кислорода, водяных паров и других газов, поэтому парциальные скорости связаны соотношением: 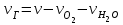 (6.7.9) (6.7.9)Физические и химические превращения в спекаемом слое агломерационной шихты протекают во времени τ и в пространстве (по высоте слоя, пространственная координата Z). Эти динамические процессы (сушка, горение углерода, изменение температуры, концентрации кислорода в газах, парциальной скорости водяных паров и кислорода по высоте слоя) характеризуются системой дифференциальных уравнений в частных производных по τ и Z. Скорость сушки шихты (или ее переувлажнения) пропорциональна разности относительных давлений водяных паров: по выражению (6.7.4) — для насыщенных паров, по уравнению (6.7.5) — для действительных значений ненасыщенных. 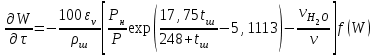 (6.7.10) (6.7.10)В процессе сушки влага мигрирует внутри частиц шихты, поэтому влажность последней необходимо учитывать: 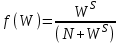 , (6.7.11) , (6.7.11)где S, N — постоянные. Эксперименты по динамике сушки агломерационной шихты показали, что N = 5,64 и S = 1,13, если W выражена в процентах на сухую массу. Для процесса переувлажнения f(W) = 1, так как в этом случае миграция влаги в частицах шихты на скорости процесса не отражается. Из уравнения материального баланса влаги следует 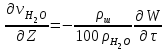 , (6.7.12) , (6.7.12)где 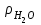 - плотность водяных паров. - плотность водяных паров.Исследования горения углерода в слое показали, что градиент концентрации кислорода в газах по высоте слоя сложным образом зависит от параметров процесса — концентрации кислорода в газе 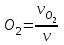 , среднего радиуса частицы топлива Rc, плотности топлива , среднего радиуса частицы топлива Rc, плотности топлива 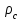 и др.: и др.: 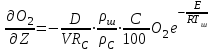 , (6.7.13) , (6.7.13)где D, R, E — постоянные. Так как текущие значения Rc и С связаны с начальными значениями 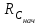 и и 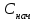 соотношением соотношением 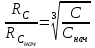 , то , то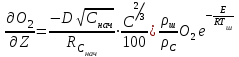 (6.7.14) (6.7.14)На основании уравнения (6.7.14) с учетом материального баланса кислорода и углерода можно записать уравнение скорости горения углерода: 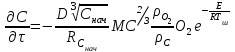 , (6.7.15) , (6.7.15)где 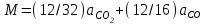 - стехиометрический коэффициент; - стехиометрический коэффициент;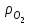 - плотность кислорода. - плотность кислорода.Из уравнений (6.14) и (6.15) получаем выражение изменения парциальной скорости кислорода по высоте слоя: 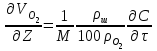 (6.7.16) (6.7.16)Составив уравнение теплового баланса газового потока, найдем градиент температуры газов по высоте слоя 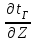 и скорость изменения температуры шихты и скорость изменения температуры шихты 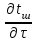 : :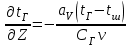 (6.7.17) (6.7.17)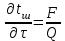 (6.7.18) (6.7.18)При этом 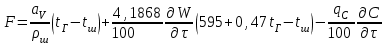 ; (6.7.19) ; (6.7.19)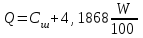 (6.7.20) (6.7.20)Уравнения (6.7.1) – (6.7.18) являются аналитической основой математического динамического моделирования агломерационного процесса на ЭВМ. Расчетная схема модели спекаемого слоя представлена на рисунке 6.7.1. 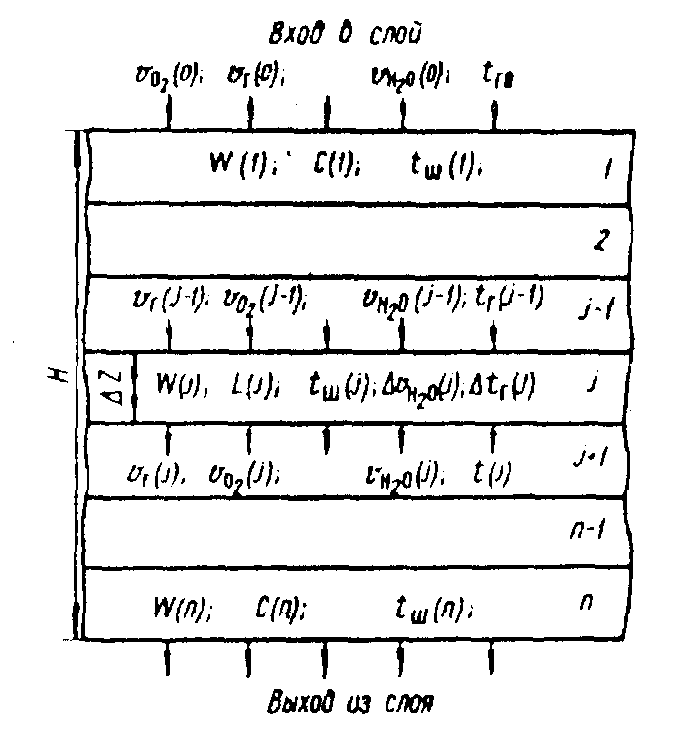 Рис. 6.7.1 - Расчетная схема модели спекаемого слоя агломерационной шихты Слой шихты высотой Н разбит на n зон, так что ∆Z=H/n. Слои пронумерованы по ходу процесса спекания (сверху вниз): 1, 2, … , j –1 , j , j + 1, … , n – 1, n. Дискретизация процесса моделирования во времени с шагом дискретности ∆τ позволяет производить расчеты по шагам, номера которых 1, 2, … , К – 1, К, К + 1, … . В результате квантования процесса во времени и в пространстве ∆Z дифференциальные уравнения (6.7.11) – (6.7.18) представлены в конечно-разностной форме. Запишем итерационную схему функционирования динамической модели. Для величин, относящихся к шихте (W, C, tш), например, для влажности: 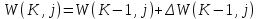 , а для величин, относящихся к газовому потоку , а для величин, относящихся к газовому потоку 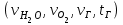 , например для скорости водяных паров: , например для скорости водяных паров: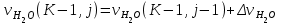 (6.7.21) (6.7.21)Для шихты номер j соответствует элементу разбиения; для газового потока номер j – 1 означает вход в элементарный слой с номером j, а номер j – выход из него. Перейдем в дифференциальных уравнениях (6.7.10) - (6.7.18) к конечным разностям (от 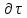 к к 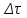 и от и от 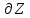 к к 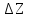 ) и выберем ) и выберем 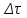 и и 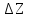 достаточно малыми. Тогда приращения достаточно малыми. Тогда приращения 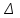 величин W, C, величин W, C, 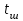 , , 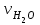 , , 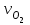 , , 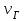 и и 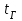 можно представить в виде: можно представить в виде: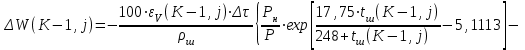 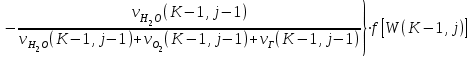 ; (6.7.22) ; (6.7.22)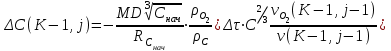 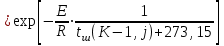 ; (6.7.23) ; (6.7.23)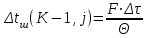 ; (6.7.24) ; (6.7.24)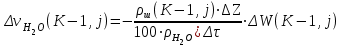 ; (6.7.25) ; (6.7.25)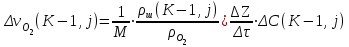 ; (6.7.26) ; (6.7.26)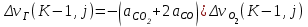 ; (6.7.27) ; (6.7.27)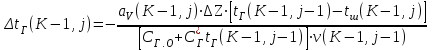 , (6.7.28) , (6.7.28)Где 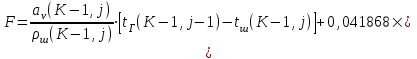 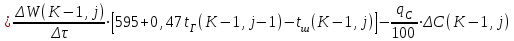 ; (6.7.29) ; (6.7.29)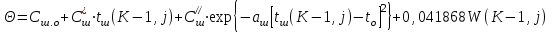 (6.7.30) (6.7.30)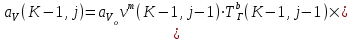 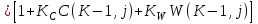 ; (6.7.31) ; (6.7.31)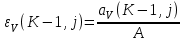 (6.7.32) (6.7.32)Изменение скорости просасываемого через слой воздуха 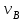 при моделировании принято таким же, как и в производственных условиях, в которых установлена эмпирическая зависимость (парабола четвертой степени): при моделировании принято таким же, как и в производственных условиях, в которых установлена эмпирическая зависимость (парабола четвертой степени):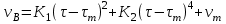 , (6.7.33) , (6.7.33)где 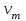 - минимальный расход в момент времени - минимальный расход в момент времени 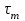 ; ;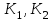 - постоянные. - постоянные.В процессе программирования расчетов на ЭВМ предусмотрены логические операции по ограничению величин С≥0 и W≥0 это позволяет обеспечить абсолютную устойчивость процесса вычислений. |
