коробок. Регрессионный и корреляционный анализ результатов эксперимента
 Скачать 47.22 Kb. Скачать 47.22 Kb.
|
Кафедра Технической механики по курсу: «Основы планирования и проведения эксперимента» Реферат на тему: регрессионный и корреляционный анализ результатов эксперимента. Выполнил студент группы Проверил Содержание Введение 2 1. Корреляционный анализ 3 1.2 Этапы корреляционного анализа 5 1.3 Коэффициенты корреляции 5 1.4 Основные свойства коэффициентов корреляции 7 1.5 Проверка значимости коэффициентов корреляции 7 2.Регрессионный метод оценки 8 2.1 Понятие регрессионного анализа 8 2.2Задачи регрессионного анализа 8 2.3Этапы регрессионного анализа 9 Заключение 12 Список используемых источников 13 ВведениеПланирование эксперимента -математико-статистическая дисциплина, изучающая методы рациональной организации экспериментальных исследований — от оптимального выбора исследуемых факторов и определения собственно плана эксперимента в соответствии с его целью до методов анализа результатов. Начало планирования эксперимента положили труды английского статистика Р.Фишера (1935), подчеркнувшего, что рациональное планирование экспериментадаёт не менее существенный выигрыш в точности оценок, чем оптимальная обработка результатов измерений. В 60-х годах 20 века сложилась современная теория планирования эксперимента. Её методы тесно связаны с теорией приближения функций и математическим программированием. Построены оптимальные планы и исследованы их свойства для широкого класса моделей. Планирование эксперимента – выбор плана эксперимента, удовлетворяющего заданным требованиям, совокупность действий направленных на разработку стратегии экспериментирования (от получения априорной информации до получения работоспособной математической модели или определения оптимальных условий). Это целенаправленное управление экспериментом, реализуемое в условиях неполного знания механизма изучаемого явления. В процессе измерений, последующей обработки данных, а также формализации результатов в виде математической модели, возникают погрешности и теряется часть информации, содержащейся в исходных данных. Применение методов планирования эксперимента позволяет определить погрешность математической модели и судить о ее адекватности. Если точность модели оказывается недостаточной, то применение методов планирования эксперимента позволяет модернизировать математическую модель с проведением дополнительных опытов без потери предыдущей информации и с минимальными затратами. Цель планирования эксперимента – нахождение таких условий и правил проведения опытов при которых удается получить надежную и достоверную информацию об объекте с наименьшей затратой труда, а также представить эту информацию в компактной и удобной форме с количественной оценкой точности. Среди основных методов анализа эксперимента, используют: - корреляционный анализ; - регрессивный анализ 1. Корреляционный анализ1.1 Суть корреляционного анализа Исследователя нередко интересует, как связаны между собой две или большее количество переменных в одной или нескольких изучаемых выборках. Например, может ли рост влиять на вес человека или может ли давление влиять на качество продукции? Такого рода зависимость между переменными величинами называется корреляционной, или корреляцией. Корреляционная связь - это согласованное изменение двух признаков, отражающее тот факт, что изменчивость одного признака находится в соответствии с изменчивостью другого. Известно, например, что в среднем между ростом людей и их весом наблюдается положительная связь, и такая, что чем больше рост, тем больше вес человека. Однако из этого правила имеются исключения, когда относительно низкие люди имеют избыточный вес, и, наоборот, астеники, при высоком росте имеют малый вес. Причиной подобных исключений является то, что каждый биологический, физиологический или психологический признак определяется воздействием многих факторов: средовых, генетических, социальных, экологических и т.д. Корреляционные связи - это вероятностные изменения, которые можно изучать только на представительных выборках методами математической статистики. Оба термина - корреляционная связь и корреляционная зависимость - часто используются как синонимы. Зависимость подразумевает влияние, связь - любые согласованные изменения, которые могут объясняться сотнями причин. Корреляционные связи не могут рассматриваться как свидетельство причинно-следственной зависимости, они свидетельствуют лишь о том, что изменениям одного признака, как правило, сопутствуют определенные изменения другого. Корреляционная зависимость - это изменения, которые вносят значения одного признака в вероятность появления разных значений другого признака. Задача корреляционного анализа сводится к установлению направления (положительное или отрицательное) и формы (линейная, нелинейная) связи между варьирующими признаками, измерению ее тесноты, и, наконец, к проверке уровня значимости полученных коэффициентов корреляции. Корреляционные связи различаютсяпо форме, направлению и степени (силе). По форме корреляционная связь может быть прямолинейной или криволинейной. Прямолинейной может быть, например, связь между количеством тренировок на тренажере и количеством правильно решаемых задач в контрольной сессии. При повышении мотивации эффективность выполнения задачи сначала возрастает, затем достигается оптимальный уровень мотивации, которому соответствует максимальная эффективность выполнения задачи; дальнейшему повышению мотивации сопутствует уже снижение эффективности. 1.2 Этапы корреляционного анализа Практическая реализация корреляционного анализа включает следующие этапы: а) постановка задачи и выбор признаков; б) сбор информации и ее первичная обработка (группировки, исключение аномальных наблюдений, проверка нормальности одномерного распределения); в) предварительная характеристика взаимосвязей (аналитические группировки, графики); г) устранение мультиколлинеарности (взаимозависимости факторов) и уточнение набора показателей путем расчета парных коэффициентов корреляции; д) исследование факторной зависимости и проверка ее значимости; е) оценка результатов анализа и подготовка рекомендаций по их практическому использованию. 1.3 Коэффициенты корреляции Коэффициенты корреляции является общепринятой в математической статистике характеристикой связи между двумя случайными величинами. Коэффициент корреляции - показатель степени взаимозависимости, статистической связи двух переменных; изменяется в пределах от -1 до +1. Значение коэффициента корреляции 0 указывает на возможное отсутствие зависимости, значение +1 свидетельствует о согласованности переменных. Различают следующие коэффициенты корреляции: - дихотомический - показатель связи признаков (переменных) измеряемых по дихотомическим шкалам наименований; - Пирсона (Pearson product-moment correlation) - коэффициент корреляции, используемый для континуальных переменных; - ранговой корреляции Спирмена (Spearmen's rank-order correlation) - коэффициент корреляции для переменных, измеренных в порядковых (ранговых) шкалах; - точечно-бисериальной корреляции (point-biserial correlation) - коэффициент корреляции, применяемый в случае анализа отношения переменных, одна из которых измерена в континуальной шкале, а другая - в строго дихотомической шкале наименований; - j - коэффициент корреляции, используемый в случае, если обе переменные измерены в дихотомической шкале наименований. - тетрахорический (четырехпольный) (tetrachoric) - коэффициент корреляции, используемый в случае, если обе переменные измерены в континуальных шкалах. Линейная связь между переменными Xi и Xj оценивается коэффициентом корреляции: 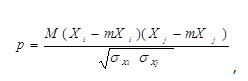 где Xi и Xj – исследуемые переменные; mXi и mXj – математические ожидания переменных; σX и σX – дисперсии переменных. Выборочный коэффициент корреляции определяют по формуле: или по преобразованной формуле: 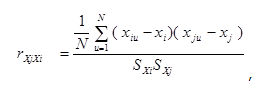 \ \или по преобразованной формуле: 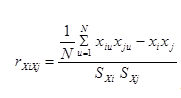 где i =1, 2, ., n, j = 1, 2, ., m, u = 1, 2, ., N; N – число опытов(объем выборки); xi, xj – оценки математических ожиданий; SXi, SXj – оценки среднеквадратических отклонений. Только при совместной нормальной распределенности исследуемых случайных величин Xi и Xj коэффициент корреляции имеет определенный смысл связи между переменными. В противном случае коэффициент корреляции может только косвенно характеризовать эту связь[5]. 1.4 Основные свойства коэффициентов корреляции К основным свойствам коэффициента корреляции необходимо отнести следующие: - коэффициенты корреляции способны характеризовать только линейные связи, т.е. такие, которые выражаются уравнением линейной функции. При наличии нелинейной зависимости между варьирующими признаками следует использовать другие показатели связи; - значения коэффициентов корреляции – это отвлеченные числа, лежащее в пределах от —1 до +1, т.е. -1 < r < 1; - при независимом варьировании признаков, когда связь между ними отсутствует, r = 0; - при положительной, или прямой, связи, когда с увеличением значений одного признака возрастают значения другого, коэффициент корреляции приобретает положительный знак и находится в пределах от 0 до +1, т.е. 0 < r < 1; - при отрицательной, или обратной, связи, когда с увеличением значений одного признака соответственно уменьшаются значения другого, коэффициент корреляции сопровождается отрицательным знаком и находится в пределах от 0 до –1, т.е. -1 < r <0; - чем сильнее связь между признаками, тем ближе величина коэффициента корреляции к 1. Если r = ±1, то корреляционная связь переходит в функциональную, т.е. каждому значению признака Х будет соответствовать одно или несколько строго определенных значений признака Y; - только по величине коэффициентов корреляции нельзя судить о достоверности корреляционной связи между признаками. Этот параметр зависит от числа степеней свободы f = n –2, где n – число коррелируемых пар показателей Х и Y. Чем больше n, тем выше достоверность связи при одном и том же значении коэффициента корреляции. [2] 1.5 Проверка значимости коэффициентов корреляции Для проверки значимости коэффициентов корреляции чаще всего используют распределение Стьюдента и условие: 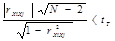 , f = N – 2, α = 0,05. , f = N – 2, α = 0,05.Если условие выполняется, то гипотеза об отсутствии корреляционной связи принимается. Регрессионный метод оценки 2.1 Понятие регрессионного анализаЭто группа методов, направленных на выявление и математическое выражение тех изменений и зависимостей, которые имеют место в системе случайных величин. Если такая система моделирует педагогическую, психологическую, биологическую и т. п., то, следовательно, путем регрессионного анализа выявляются и математически выражаются явления научного эксперимента и зависимости между ними. Характеристики этих явлений измеряются в разных шкалах, что накладывает ограничения на способы математического выражения изменений и зависимостей, которые изучаются исследователем. Методы регрессионного анализа рассчитаны, главным образом, на случай устойчивого нормального распределения, в котором изменения от опыта к опыту проявляются лишь в виде независимых испытаний. Задачи регрессионного анализа Выделяются различные формальные задачи регрессионного анализа. Они могут бы ть простыми или сложными по формулировкам, по математическим средствам и трудоемкости. Перечислим и рассмотрим на примерах те из них, которые представляются основными. Первая задача – выявить факт изменчивости изучаемого явления при определенных, но не всегда четко фиксированных условиях. Вторая задача – выявить тенденцию как периодическое изменение признака. Третья задача – это выявление закономерности, выраженной в виде корреляционного уравнения (регрессии). Линейная модель парной регрессии Регрессия – функция, позволяющая по величине одного корреллируемого признака определить среднюю величину другого признака. Этапы регрессионного анализа Выделим основные этапы регрессионного анализа. Первый этап. Предположение. На этом этапе происходит выбор формы связи между переменными (модель). Второй этап. Параметризация – происходит оценка значений параметра в выбранной формуле статистической связи. Форма связи (функция) линейная, нелинейная. Третий этап. Проверка надёжности полученных оценок. На этом этапе осуществляются следующие тесты: F-тест (проверка статистической значимости выбранной формы связи), t-тест (проверка статистической значимости найденных числовых значений параметра). В результате анализа статистических данных, выбора и построения модели последовательно выполняются все три этапа. Формально могут возникать ситуации двух типов: 1. Вид функциональной зависимости неизвестен. В этом случае нужно решить предварительно задачу, направленную на отыскание подходящей функциональной зависимости. Это достаточно сложная задача, но она успешно решается современными средствами информационных технологий (программа Excel). 2.Вид функциональной зависимости известен и требуется только найти ее параметры (коэффициенты регрессии b 0 , b 1 , b 2 , …). Термином линейный регрессионный анализ обозначают такое прогнозирование, которое описывается линейной взаимосвязью между исследуемыми переменными: y = b0 + b1x. При всем разнообразии эмпирических формул все же имеется вид аналитической зависимости, получивший широкое распространение. Им является уравнение регрессии в виде многочленов (полинома), расположенных по восходящим степеням изучаемого фактора и одновременно линейных ко всем коэффициентам. Такая формула имеет вид: y = f(x) = b0 + b1x + b2x2 +…+bm 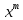 , ,где b0 , b1 , b2 ,…, bm − коэффициенты, подлежащие определению. Этот ряд − сходящийся, т.к. стремится к некоторому пределу. Эмпирические формулы (аппроксимирующие уравнения) всегда имеют ограниченную область применения, которая не должна выходить за пределы имеющихся опытных данных. Широкое применение аппроксимирующих уравнений объясняется следующими причинами: 1. Точное аналитическое выражение зависимости между исследуемыми величинами может оставаться неизвестным и поэтому по необходимости приходится ограничиваться приближенными формулами эмпирического характера. 2. Точная функциональная зависимость выражается формулой настолько сложной, что ее непосредственное применение при вычислениях было бы очень затруднительным. Эмпирические формулы могут быть разнообразными, т.к. при выборе аналитической зависимости руководствуются не какими-то строгими теориями (физическими или экономическими), а ставят только одно условие −возможно близкое соответствие значений, вычисленных по формуле опытным данным. Таким образом, формально описание одного и того же процесса можно дать разными по виду уравнениями. Их пригодность оценивается только по одному критерию − наиболее точное предсказание экспериментального результата. В эмпирическую формулу можно вводить различное число постоянных параметров (коэффициентов), величину которых нужно определить с большой точностью. Более удачными (удобными) следует считать уравнения с небольшим числом коэффициентов (не более 2−3). В противном случае возрастают трудности с применением таких формул. 2.4 Метод наименьших квадратов Для определения коэффициентов уравнения регрессии b применяют разные методы (графический, метод средних), однако наибольшее распространение получил метод наименьших квадратов (МНК). Экспериментальные данные о значениях переменных х и у приведены в таблице
В результате их выравнивания получена функция Используя метод наименьших квадратов , аппроксимировать эти данные линейной зависимостью y=ax+b (найти параметры а и b). Выяснить, какая из двух линий лучше (в смысле метода наименьших квадратов) выравнивает экспериментальные данные. Суть метода наименьших квадратов Задача заключается в нахождении коэффициентов линейной зависимости, при которых функция двух переменных а и b 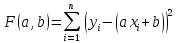 принимает наименьшее значение. То есть, при данных а и b сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. В этом вся суть метода наименьших квадратов. Таким образом, решение примера сводится к нахождению экстремума функции двух переменных. Заключение Любой показатель практически зависит от бесконечного количества факторов. Однако лишь ограниченное количество факторов действительно существенно воздействуют на исследуемый показатель. Доля влияния остальных факторов столь незначительна, что их игнорирование не может привести к существенным отклонениям в поведении исследуемого объекта. Выделение и учет в модели лишь ограниченного числа реально доминирующих факторов является важной задачей качественного анализа, прогнозирования и управления ситуаций. Если в естественных науках большей частью имеют дело со строгими (функциональными) зависимостями, при которых каждому значению одной переменной соответствует единственное значение другой, то между экономическими переменными, в большинстве случаев, таких зависимостей нет и дело имеют с корреляционными зависимостями. Корреляционно-регрессионные модели, какими бы сложными они не были, не скрывают полностью всех причинно-следственных связей, однако достаточно адекватно могут описывать влияние на результативный признак существенных факторов, если проведен предварительный анализ сущности и специфики исследуемых явлений и процессов. Таким образом, корреляционный и регрессионный анализ позволяет определить зависимость между факторами, а так же проследить влияние задействованных факторов. Эти показатели имеют широкое применение в обработке статистических данных Список используемых источников Н.Ш. Кремер. Теория вероятностей и математическая статистика. - М.:2000г Пугачёв В.С., «Теория вероятностей и математическая статистика», – М.: «Инфра–М», 2004. Замков О.О., Толстопятенко А.В., Черемных Р.Н., «Математические методы в экономике», – М.: «Дис», 2003; |
