Дисперсионный анализ. Дисперсионный анализ (конспект). Регулируемые (или контролируемые) и неконтролируемые

• Название: Регулируемые (или контролируемые) и неконтролируемые
• Анкор: Дисперсионный анализ
• Дата: 16.01.2021
• Размер: 27.8 Kb.
• Имя файла: Дисперсионный анализ (конспект).docx
• Тип: Задача; #168647

Работа №12. Дисперсионный анализ

Все факторы , влияющие на величину какого-либо биологического признака, подразделяют на регулируемые (или контролируемые) и неконтролируемые.

Величина воздействия первой группы факторов может быть задана исследователем (доза облучения , концентрация раствора , температура химической реакции и т.д.) или измерена (солнечная освещённость, влажность воздуха, содержание солей в водоеме и т.д.)

Неконтролируемые факторы обычно варьируют случайным образом; порою эффект от их воздействия на биологические объекты не поддается учету, хотя сами факторы могут быть количественно оценены (вспышки на Солнце , атмосферное давление и др.)

Влияние неконтролируемых факторов затрудняет выявление связи между величинами признака и регулируемого фактора. Задача ещё более усложняется в том случае, когда на объект действует не один , а два и более регулируемых фактора и необходимо установить , какой из этих факторов влияет на определённый признак , а какой не влияет.

Для решения такого рода задач Р.А. Фишер(1925г) предложил метод , который называется дисперсионным анализом . Сущность этого метода заключается в том , что результаты экспериментов оцениваются не по средним арифметическим , а по дисперсиям. Величина общей вариации признака D_y состоит из двух слагаемых:

Вариации D_x , обусловленной действием регулируемого (контролируемого) фактора

ВариацииD_z ,обусловленной действием неконтролируемого фактора.

D_y= D_x +D_z

Задача состоит в том , что чтобы найти общую дисперсию для всего комплекса наблюдений и разложить ее на составляющие части .

Перед началом анализа исходные данные группирует в комплексы, представляемые в форме таблиц. В зависимости от числа факторов , по которым производится анализ , комплексы подразделяют на однофакторные , двухфакторные и многофакторные. Анализ во всех случаях проводится по некоторым общим схемам. Достоверность влияния регулируемого фактора на рассматриваемый признак оценивается с помощью критерия Фишера (фактического)

F_ф=σ²_x/σ²_z ,

Где σ²_x-межгрупповая дисперсия,

σ²_z – внутригрупповая дисперсия.

Вычисленное значение критерия Фишера сравнивается со стандартным (Fcт), найденным в таблице П-6 Приложения для соответствующего числа степеней свободы и принятого уровня значимости. Если фактическое значение критерия Фишера Fф ≥ Fcт , то заключение о влиянии регулируемого фактора на рассматриваемый признак достоверно .

Одним из путей повышения значения Fф (за счёт снижения σ²_z) является использование генетически однородного материала( определенного штамма микроорганизмов , сорта растений , линии мышей , крыс и т.д)

Дисперсионный анализ однофакторных комплексов

Дисперсионный анализ проводится по следующей схеме:

1. 
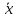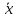   Вычисляют среднюю арифметическую всего комплекса(общую среднюю) и частные (групповые) средние _i для соответствующих градаций фактора. Полученные значения групповых средних вносят в таблицу
   
2. 
   Определяют общую сумму квадратов отклонений: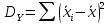
   

3. 
   Вычисляют межгрупповую сумму квадратов отклонений: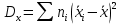
   

, где n_i- статистический вес групповых средних (число повторностей )

4. 
   Находят внутригрупповую (остаточную) сумму квадратов отклонений
   

5. 
   Устанавливают числа степеней свободы:
   

Для общей дисперсии Ку=N-1

Для межгрупповой дисперсии Кх=а-1

Для внутригрупповой дисперсии Кz= N-a ,

Где N-общее число значений признака , а-число градаций фактора.

6. 
   Вычисляют значение дисперсий:
   

Общая σ²_Y=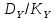

Межгрупповая σ²_x=

Внутригрупповая(остаточная) σ²_z=

7. 
   Для установления достоверности заключения вычисляют критерий Фишера:
   

Fф= σ²_x/ σ²_z

8. 
   В таблице П-6 приложения для числа k1=K_x и k2=K_z находят значения критерия Фишера – Fст для Р=0,05 и Fст для Р=0,01.
   

Если Fф ≥ Fcт , то влияние регулируемого фактора на рассматриваемый признак можно считать достоверным .

Дисперсионный анализ двухфакторных комплексов

Анализ проводят в следующем порядке :

1. 
   Все варианты комплекса суммируют. Найденную сумму возводят в квадрат и делят на общее число наблюдений N:
   

2. 
   Каждую варианту возводят в квадрат и находят сумму квадратов
   

3. 
   Находят сумму квадратов отклонений , общую для всего комплекса:
   

4. 
   Для каждой клетки находят сумму чисел , возводят ее в квадрат и делят на число повторностей n_i .Полученные результаты суммируют для всех клеток: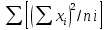
   

5. 
   Находим межгрупповую сумму квадратов отклонений:
   

6. 
   Определяют внутригрупповую сумму квадратов отклонений:
   

7. 
   Находят сумму квадратов отклонений:
   

• 
  По фактору А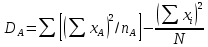
  

• 
  По фактору В
  

• 
  По взаимодействию фактора А и В:
  

8. 
   Определяем число степеней свободы:
   

K_A=a-1 K_B=b-1

K_AB=(a-1)*(b-1)=K_A * K_B

K_Z=N-ab

9. 
   Вычисляют величины дисперсий:
   

σ²_A=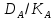

σ²_B=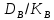

σ²_AB=

σ²_Z=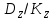

10. 
    Определяют значения критерия Ыишера (фактические):
    

• 
  По фактору А Fф^А= σ²_А/ σ²_z
  
• 
  По фактору В Fф^В= σ²_В/ σ²_z
  
• 
  По совместному действию факторов АВ Fф^АВ= σ²_АВ/ σ²_z
  

Соответствующие стандартные значения критерия Фишера для уровня значимости Р=0,01 находят в таблице П-6 Приложения

Если все стандартные значения критерия Фишера меньше соответствующих фактических значений , то это свидетельствует о том , что оба фактора в отдельности и совместно с достоверностью выше 0,99 влияют на рассматриваемый признак

-