ALIKHAN BOKEIKHAN UNIVERSITY

СРО
тема: «Рекурсия и двумерные массивы»
Выполнил(a) Акежан А.М ВТ-202С
Проверил(а)Назарова.В.В
Семей 2022г.
Содержание
Содержание 2
Введение 2
Работа с рекурсией в Python 4
Использование рекурсии в Python 5
Пример рекурсивной функции в Python 5
Типы рекурсии в Python 6
Пример хвостового рекурсивного вызова 6
Рекурсия в Python с числами 8
Факториал числа 8
найти n-е число в ряду Фибоначчи 8
Обращение целых чисел 9
Рекурсия в Python со строками и массивами 9
Рекурсия в Python со структурами данных 10
Что такое 2D массив в Python и его использование 11
Пример обхода 11
Вставка массива в 2D массив. 12
Вставка элемента во внутренний массив. 12
Удаление одного элемента 13
Удаление внутреннего массива 14
15
Заключение 16
Введение
Что произойдет, если мы разместим два зеркала параллельно друг другу? Вы увидите несколько изображений, растянутых до бесконечности, вызванных отражениями между поверхностями. Представьте, что вы хотите узнать имя человека в очереди, в которой вы стоите. Вы просите людей узнать об этом. Они продолжают спрашивать следующего человека, пока не найдут ответ. Как только ответ найден, они отправляют его обратно, пока он не дойдет до вас. Два приведенных выше примера изображают процесс, в котором определенное действие повторяется до тех пор, пока не будет выполнено условие. Эти процессы имеют сильное сходство с тем, что мы называем рекурсией. Процесс, в котором функция вызывает саму себя, называется рекурсией. Этот процесс помогает упростить метод решения проблем, заменяя итеративный код рекурсивными операторами.
2D массив в python - это двумерная структура данных, используемая для хранения данных, как правило, в табличном формате. Например, если вы хотите сохранить матрицу и выполнить некоторые вычисления, как бы вы это сделали на Python? Ну, ответ заключается в использовании 2D массивов в Python. Читайте дальше, чтобы узнать больше.
Работа с рекурсией в Python
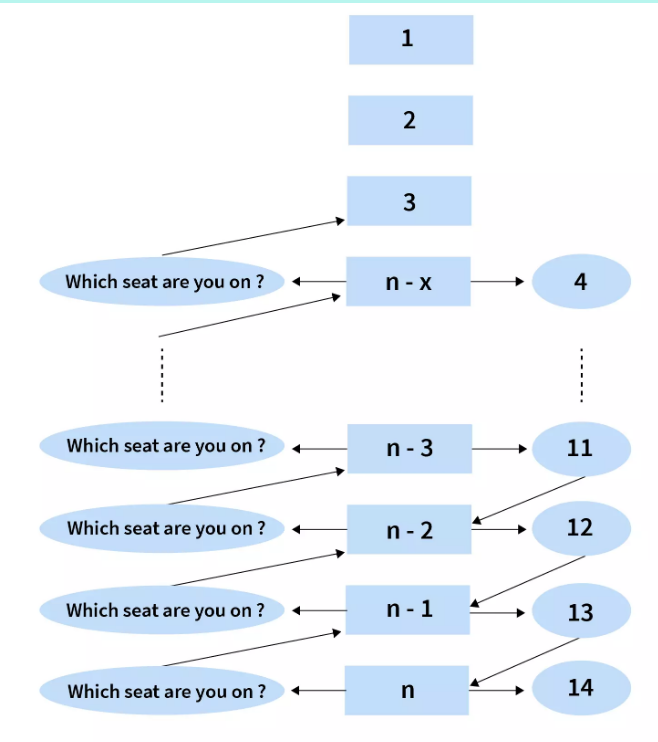
Представьте, что вы сидите в аудитории и не понимаете, в каком ряду вы сидите. Поскольку вы не можете считать до первой скамейки, вы спрашиваете человека прямо перед вами, в каком ряду он сидит. Если человек не знает номер своего места, он спросит человека прямо перед ним.
Процесс запроса будет продолжаться до тех пор, пока кто-нибудь не узнает номер своего места. Как показано на приведенной выше диаграмме, когда человек в 3-м ряду сообщает, что он сидит в ряду 3, человек позади него добавит единицу и передаст свой номер в ряду 4 человеку сразу после него. Номер строки будет вычислен в каждой строке и будет передаваться до тех пор, пока он не дойдет до вас. Как только он дойдет до вас, добавьте 1, чтобы получить свой окончательный номер строки. Именно так работает рекурсия в Python.
Использование рекурсии в Python
Довольно часто люди задаются вопросом, почему мы должны использовать рекурсию, когда существуют циклы. Все может быть закодировано без рекурсии. Разница между итерацией и рекурсией заключается в том, что у рекурсивного кода нет последовательного завершения. Он проверяет базовое условие и может продолжаться до тех пор, пока оно выполняется. Рекурсия в python используется, когда задачи можно разбить на более простые части для упрощения вычислений и более читаемого кода.
Например, если вы хотите найти ученика в школе, это можно сделать двумя способами. Вы могли бы собрать всех студентов в аудитории, а затем искать ее по одному. Более простой метод разделил бы школу на разделы до тех пор, пока не будет создан наименьший раздел для поиска ученика, т. Е. Было бы разумнее сначала выполнить поиск по классу, в котором она учится, затем по классу, и тогда вы сможете гораздо легче найти ее местоположение. Хотя обнаружено, что рекурсия в некоторых случаях дает результаты быстрее при правильной оптимизации, она также может увеличить использование памяти.
Таким образом, рекурсию следует использовать только при необходимости.
Пример рекурсивной функции в Python
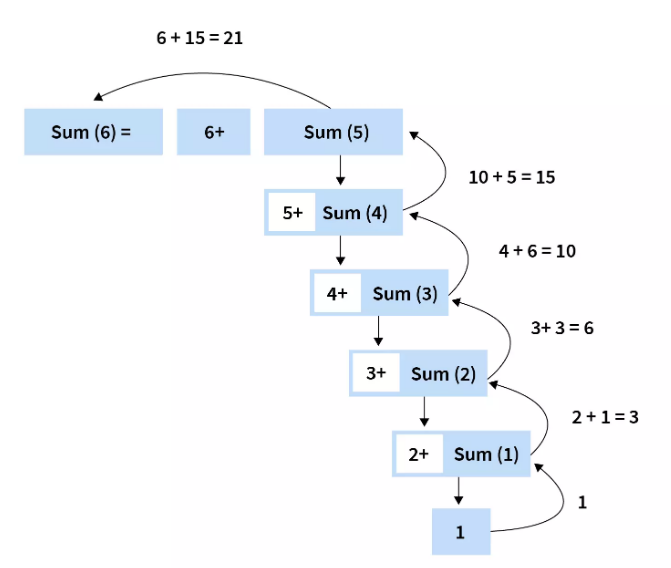
Предположим, вы хотите найти сумму n натуральных чисел. Мы бы написали следующий код, чтобы получить ответ. Мы бы написали следующий код, чтобы получить ответ.
def sum(n):
if n <= 1:
return n
else:
ans = sum(n - 1)
return n + ans
print(sum(6))
Вывод 21
Типы рекурсии в Python
Существует в основном 2 типа рекурсивных функций:
1) Прямая рекурсия -
В этом типе рекурсии функция вызывает саму себя.
a) Хвостовая рекурсия - рекурсивный вызов называется хвостово-рекурсивным, если это последний оператор, который выполняется внутри функции.
Пример хвостового рекурсивного вызова
Следующая функция выводит натуральные числа из n в порядке убывания. Это делается путем перемещения цифр от n до 1 и возврата каждой цифры при вызове. В этом примере позиция оператора print имеет первостепенное значение. Базовый вариант будет равен 0, где вызову не будет возвращено значение.
При первом вызове функции оператор print выводит на экран 5, а disp(4) добавляется в верхнюю часть стека. При следующем вызове печатается 4, а disp(5) добавляется в стек.
Аналогично, 3, 2 и 1 печатаются в следующих вызовах. При последнем вызове значение n становится равным 0, и, таким образом, выполняется базовый вариант, что приводит к завершению рекурсии.В последнем вызове значение n становится 0, и, таким образом, выполняется базовый вариант, что приводит к завершению рекурсии.
def dispn(n):
if n == 0:
return
print(n)
dispn(n – 1)
dispn(5)
Вывод:
5
4
3
2
1
Пример хвостового рекурсивного вызова
def GCD(a, b):
if b == 0:
return a
return GCD(b, a % b)
print(GCD(49, 35))
Вывод:7
def A(n):
if n > 0:
print("", n, end='')
B(n + 1)
def B(n):
if n > 1:
print("", n, end='')
A(n - 5)
A(20)
Вывод: 20 21 16 17 12 13 8 9 4 5
Рекурсия в Python с числами
def isDivisibleBy7(num):
if num < 0:
return isDivisibleBy7(-num)
if num == 0 or num == 7:
return True
if num < 10:
return False
return isDivisibleBy7(num // 10 - 2 * (num - num // 10 * 10))
print(isDivisibleBy7(63))
print(isDivisibleBy7(23))
Вывод True False
Факториал числа
def fact(n):
if n == 1:
return n
else:
return n * fact(n - 1)
print(fact(5))
Вывод:120
найти n-е число в ряду Фибоначчи
def fib(n):
if n == 0:
return 0
elif n == 1 or n == 2:
return 1
return (fib(n - 1) + fib(n - 2))
print(fib(8))
Вывод 21
Обращение целых чисел
res = 0
start = 1
def reverseDigits(num):
global res
global start
if num > 0:
reverseDigits(int(num / 10))
res += (num % 10) * start
start *= 10
return res
print(reverseDigits(524))
Вывод 425
Рекурсия в Python со строками и массивами
def isAscending(arr):
n = len(arr)
if n == 1 or n == 0:
return True
return arr[0] <= arr[1] and isAscending(arr[1:])
arr=[1,4,2,3,5]
print(isAscending(arr))
arr=[1,2,3,4,5]
print(isAscending(arr))
Вывод false true
Рекурсия в Python со структурами данных
class Node:
def __init__(self, data):
self.data = data
self.next = None
def newNode(data):
new_node = Node(data)
new_node.data = data
new_node.next = None
return new_node
def insertEnd(head, data):
if (head == None):
return newNode(data)
else:
head.next = insertEnd(head.next, data)
return head
def traverse(head):
if (head == None):
return
print(head.data, end=" ")
traverse(head.next)
head = None
head = insertEnd(head, 6)
head = insertEnd(head, 8)
head = insertEnd(head, 10)
head = insertEnd(head, 12)
head = insertEnd(head, 14)
traverse(head)
Вывод 6 8 10 12 14
Что такое 2D массив в Python и его использование
2D массив в python - это двумерная структура данных, линейно хранящаяся в памяти. Это означает, что он имеет два измерения, строки и столбцы, и, следовательно, он также представляет собой матрицу. Под линейной структурой данных мы подразумеваем, что элементы линейно размещаются в памяти, и каждый элемент связан со своими предыдущими и следующими элементами.
Мы визуализируем 2D массив в табличном формате, но на самом деле элементы хранятся в памяти линейно. Элементы 2D массива последовательно размещаются в памяти. Это означает, что если один элемент присутствует по текущему адресу памяти, следующий элемент будет помещен по следующему адресу памяти. Этот тип хранилища делает массивы доступными случайным образом. Это означает, что мы можем получить доступ к любому элементу массива независимо.
Пример
arr=[[1,2,3],[4,5,6],[7,8,9]]
print("Element at [2]=",arr[2])
Вывод Element at [2]= [7, 8, 9]
Пример обхода
arr=[[1,2,3],[4,5,6],[7,8,9]]
for _ in arr:
for i in _:
print(i,end=" ")
print()
Вывод:
1 2 3
4 5 6
7 8 9
Вставка массива в 2D массив.
from array import *
arr=[[1,2,3],[4,5,6],[7,8,9]]
arr.insert(2,[11,12,13])
for _ in arr:
for i in _:
print(i,end=" ")
print()
Вывод
1 2 3
4 5 6
11 12 13
7 8 9
Вставка элемента во внутренний массив.
from array import *
arr=[[1,2,3],[4,5,6],[7,8,9]]
print("Original Array")
for _ in arr:
for i in _:
print(i,end=" ")
print()
arr[1].insert(2,12)
print("Modified Array")
for _ in arr:
for i in _:
print(i,end=" ")
print()
Вывод:
Original Array
1 2 3
4 5 6
7 8 9
Modified Array
1 2 3
4 5 12 6
7 8 9
Удаление одного элемента
from array import *
arr=[[1,2,3],[4,5,6],[7,8,9]]
print("Original Array")
for _ in arr:
for i in _:
print(i,end=" ")
print()
del(arr[1][2])
print("Modified Array")
for _ in arr:
for i in _:
print(i,end=" ")
print()
Вывод
Original Array
1 2 3
4 5 6
7 8 9
Modified Array
1 2 3
4 5
7 8 9
Удаление внутреннего массива
from array import *
arr=[[1,2,3],[4,5,6],[7,8,9]]
print("Original Array")
for _ in arr:
for i in _:
print(i,end=" ")
print()
del(arr[1])
print("Modified Array")
for _ in arr:
for i in _:
print(i,end=" ")
print()
Вывод
Original Array
1 2 3
4 5 6
7 8 9
Modified Array
1 2 3
7 8 9
Заключение
Массив представляет собой набор линейных структур данных, которые содержат все элементы одного и того же типа данных в непрерывном пространстве памяти.
Это похоже на контейнер, который содержит определенное количество элементов, имеющих один и тот же тип данных.
Индекс массива начинается с 0, и, следовательно, программист может легко получить положение каждого элемента и выполнять различные операции над массивом.
2D массив - это массив массивов, которые могут быть представлены в виде матрицы, например, строк и столбцов. В этом массиве положение элементов данных определяется двумя индексами вместо одного индекса.
В Python мы можем получить доступ к элементам двумерного массива, используя два индекса. Первый индекс относится к индексации списка, а второй индекс относится к положению элементов. Если мы определяем только один индекс с именем массива, он возвращает все элементы 2-мерного, хранящиеся в массиве. |
 Скачать 307.41 Kb.
Скачать 307.41 Kb.


