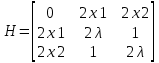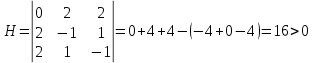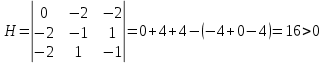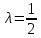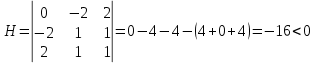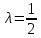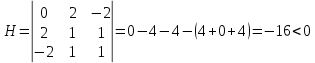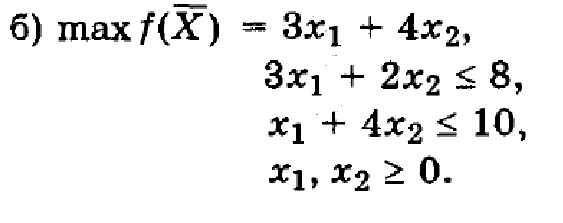
Решение
1 способ. Решаем в среде Excel с помощью команды «Поиск решения».
Создаем в Excel документ с входными данными, вызываем команду «Поиск решения» и проводим расчет (рис.2)
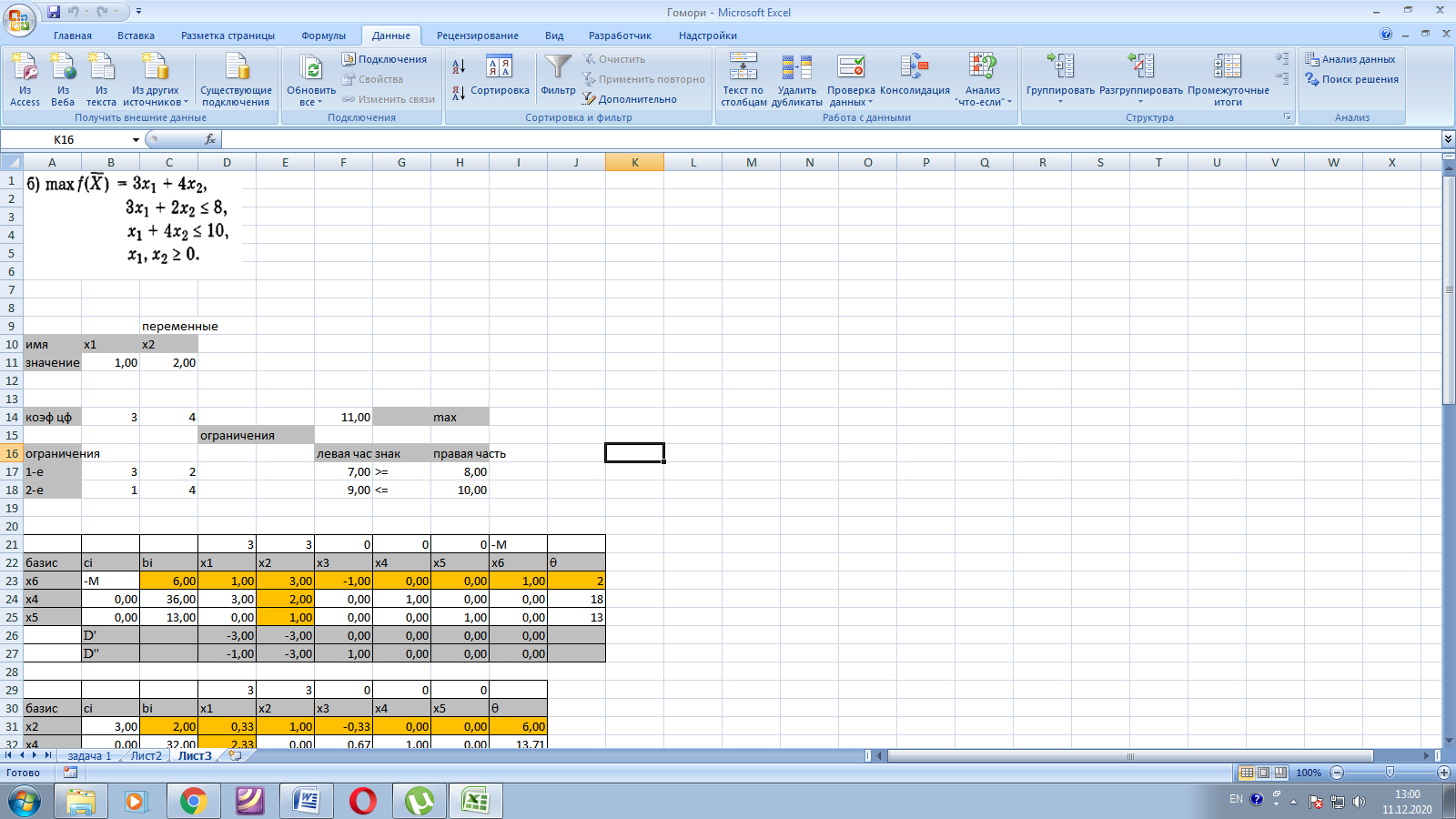
Рисунок 2 – Решение в среде Excel
Решаем задачу симплекс-методом, пока без учета условия целочисленности переменных. Приводим задачу к канонической форме.
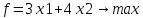
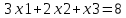
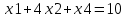
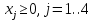
Строим симплекс-таблицу и производим расчет.
|
|
|
3
|
4
|
0
|
0
|
|
базис
|
сi
|
bi
|
x1
|
x2
|
x3
|
x4
|
q
|
x4
|
0,00
|
8,00
|
3,00
|
2,00
|
1,00
|
0,00
|
4
|
x5
|
0,00
|
10,00
|
1,00
|
4,00
|
0,00
|
1,00
|
2,5
|
|
D'
|
|
-3,00
|
-4,00
|
0,00
|
0,00
|
|
|
|
|
|
|
|
|
|
|
|
|
3
|
4
|
0
|
0
|
|
базис
|
сi
|
bi
|
x1
|
x2
|
x3
|
x4
|
q
|
x4
|
0,00
|
3,00
|
2,50
|
0,00
|
1,00
|
-0,50
|
1,20
|
x2
|
4,00
|
2,50
|
0,25
|
1,00
|
0,00
|
0,25
|
10,00
|
|
D'
|
|
-2,00
|
0,00
|
0,00
|
1,00
|
|
|
|
|
|
|
|
|
|
|
|
|
3
|
4
|
0
|
0
|
|
базис
|
сi
|
bi
|
x1
|
x2
|
x3
|
x4
|
q
|
x1
|
3,00
|
1,20
|
1,00
|
0,00
|
0,40
|
-0,20
|
|
x2
|
4,00
|
2,20
|
0,00
|
1,00
|
-0,10
|
0,30
|
|
|
D'
|
|
0,00
|
0,00
|
0,80
|
0,60
|
|
Получаем x1=1.2; x2=2.2.
План содержит дробные значения.
Составляем дополнительное ограничение по строки переменной x2.
[0]x1+[1]x2+[-0.1]x3+[0.3]x4[2.2]
0.9 x3+0.3 x4 0.2; -0,9x3-0,3x4+x5=-0,2
Добавляем это ограничение и продолжаем решение двойственным симплекс-методом.
|
|
|
3
|
4
|
0
|
0
|
0
|
|
базис
|
сi
|
bi
|
x1
|
x2
|
x3
|
x4
|
x5
|
|
x1
|
3,00
|
1,20
|
1,00
|
0,00
|
0,40
|
-0,20
|
0,00
|
|
x2
|
4,00
|
2,20
|
0,00
|
1,00
|
-0,10
|
0,30
|
0,00
|
|
x5
|
0,00
|
-0,2
|
0,00
|
0,00
|
-0,9
|
-0,3
|
1,00
|
|
|
D'
|
|
0,00
|
0,00
|
0,80
|
0,60
|
0,00
|
|
|
q
|
|
|
|
8/9
|
2
|
|
|
Выводим переменную x5 из базиса и вводим в базис переменную x3
|
|
|
|
3
|
4
|
0
|
0
|
0
|
0
|
базис
|
сi
|
bi
|
x1
|
x2
|
x3
|
x4
|
x5
|
x6
|
x1
|
3,00
|
10/9
|
1,00
|
0,00
|
0,00
|
-1/3
|
4/9
|
0
|
x2
|
4,00
|
20/9
|
0,00
|
1,00
|
0,00
|
1/3
|
-1/9
|
0
|
x3
|
0,00
|
2/9
|
0,00
|
0,00
|
1,00
|
1/3
|
-1/9
|
0
|
|
D'
|
|
0,00
|
0,00
|
0,00
|
1/3
|
8/9
|
0,00
|
Вводим дополнительное ограничение по строке переменной x3:
[0]x1+[0]x2+[1]x3+[1/3]x4+[-1/9]x5 [2/9]
-1/3*x4-8/9*x4+x6=-2/9
|
|
|
3
|
4
|
0
|
0
|
0
|
0
|
базис
|
сi
|
bi
|
x1
|
x2
|
x3
|
x4
|
x5
|
x6
|
x1
|
3,00
|
10/9
|
1,00
|
0,00
|
0,00
|
-1/3
|
4/9
|
0
|
x2
|
4,00
|
20/9
|
0,00
|
1,00
|
0,00
|
1/3
|
-1/9
|
0
|
x3
|
0,00
|
2/9
|
0,00
|
0,00
|
1,00
|
1/3
|
-1/9
|
0
|
x6
|
0
|
-2/9
|
0
|
0
|
0
|
-1/3
|
-8/9
|
1
|
|
D'
|
|
0,00
|
0,00
|
0,00
|
1/3
|
8/9
|
0,00
|
|
q
|
|
|
|
|
1
|
1
|
|
Выводим переменную x6 из базиса и вводим в базис x4
|
|
|
3
|
4
|
0
|
0
|
0
|
0
|
базис
|
сi
|
bi
|
x1
|
x2
|
x3
|
x4
|
x5
|
x6
|
x1
|
3,00
|
1,33
|
1,00
|
0,00
|
0,00
|
0,00
|
1,33
|
-1,00
|
x2
|
4,00
|
2,00
|
0,00
|
1,00
|
0,00
|
0,00
|
-1,00
|
1,00
|
x3
|
0,00
|
0,00
|
0,00
|
0,00
|
1,00
|
0,00
|
-2,00
|
1,00
|
x4
|
0,00
|
0,666667
|
0
|
0
|
0
|
1
|
2,666667
|
-3
|
|
D'
|
|
0,00
|
0,00
|
0,00
|
0,00
|
0,00
|
1,00
|
|
q
|
|
|
|
|
|
0
|
|
Вводим дополнительное ограничение по строке переменной x4:
[0]x1+[0]x2+[0]x3+[1]x4+[2.66667]x5+[-3]x6 [0.6667]
0.6667*x5 0.6667
-0.6667*x5+x7=- 0.6667
|
|
|
3
|
4
|
0
|
0
|
0
|
0
|
0
|
базис
|
сi
|
bi
|
x1
|
x2
|
x3
|
x4
|
x5
|
x6
|
x7
|
x1
|
3,00
|
1,33
|
1,00
|
0,00
|
0,00
|
0,00
|
1,33
|
-1,00
|
0,00
|
x2
|
4,00
|
2,00
|
0,00
|
1,00
|
0,00
|
0,00
|
-1,00
|
1,00
|
0,00
|
x3
|
0,00
|
0,00
|
0,00
|
0,00
|
1,00
|
0,00
|
-2,00
|
1,00
|
0,00
|
x4
|
0,00
|
0,666667
|
0
|
0
|
0
|
1
|
2,666667
|
-3
|
0,00
|
x7
|
0,00
|
-0,66667
|
0,00
|
0,00
|
0,00
|
0,00
|
-0,66667
|
0,00
|
1,00
|
|
D'
|
|
0,00
|
0,00
|
0,00
|
0,00
|
0,00
|
1,00
|
0,00
|
|
q
|
|
|
|
|
|
0
|
|
|
Выводим из базиса x7 и вводим x5
|
|
|
3
|
4
|
0
|
0
|
0
|
0
|
0
|
базис
|
сi
|
bi
|
x1
|
x2
|
x3
|
x4
|
x5
|
x6
|
x7
|
x1
|
3,00
|
0,00
|
1,00
|
0,00
|
0,00
|
0,00
|
0,00
|
-1,00
|
2,00
|
x2
|
4,00
|
3,00
|
0,00
|
1,00
|
0,00
|
0,00
|
0,00
|
1,00
|
-1,50
|
x3
|
0,00
|
2,00
|
0,00
|
0,00
|
1,00
|
0,00
|
0,00
|
1,00
|
-3,00
|
x4
|
0,00
|
-2
|
0
|
0
|
0
|
1
|
0
|
-3
|
4
|
x5
|
0,00
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
-1,5
|
|
D'
|
|
0,00
|
0,00
|
0,00
|
0,00
|
0,00
|
1,00
|
0,00
|
|
q
|
|
|
|
|
|
|
0,33
|
|
Выводим x4 вводим x6
|
|
|
3
|
4
|
0
|
0
|
0
|
0
|
0
|
базис
|
сi
|
bi
|
x1
|
x2
|
x3
|
x4
|
x5
|
x6
|
x7
|
x1
|
3,00
|
0,67
|
1,00
|
0,00
|
0,00
|
-0,33
|
0,00
|
0,00
|
0,67
|
x2
|
4,00
|
2,33
|
0,00
|
1,00
|
0,00
|
0,33
|
0,00
|
0,00
|
-0,17
|
x3
|
0,00
|
1,33
|
0,00
|
0,00
|
1,00
|
0,33
|
0,00
|
0,00
|
-1,67
|
x6
|
0,00
|
0,666667
|
0
|
0
|
0
|
-0,3333
|
0
|
1
|
-1,3333
|
x5
|
0,00
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
-1,5
|
|
D'
|
|
0,00
|
0,00
|
0,00
|
0,33
|
0,00
|
0,00
|
1,33
|
Составляем дополнительное ограничение по строке переменной x1
[1]x1+[0]x2+[0]x3+[-0.33]x4+[0]x5+[0]x6[+[0.6667]x7 [0.6667]
0.66667x3+0.66667x70.6667
0.66667x3+0.66667x7-x8=0.6667
|
|
|
3
|
4
|
0
|
0
|
0
|
0
|
0
|
0
|
базис
|
сi
|
bi
|
x1
|
x2
|
x3
|
x4
|
x5
|
x6
|
x7
|
x8
|
x1
|
3,00
|
0,67
|
1,00
|
0,00
|
0,00
|
-0,33
|
0,00
|
0,00
|
0,67
|
0,00
|
x2
|
4,00
|
2,33
|
0,00
|
1,00
|
0,00
|
0,33
|
0,00
|
0,00
|
-0,17
|
0,00
|
x3
|
0,00
|
1,33
|
0,00
|
0,00
|
1,00
|
0,33
|
0,00
|
0,00
|
-1,67
|
0,00
|
x6
|
0,00
|
0,666667
|
0
|
0
|
0
|
-0,33333
|
0
|
1
|
-1,33333
|
0,00
|
x5
|
0,00
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
-1,5
|
0,00
|
x8
|
0,00
|
-0,67
|
0
|
0
|
0
|
-0,67
|
0
|
0
|
-0,67
|
1,00
|
|
D'
|
|
0,00
|
0,00
|
0,00
|
0,33
|
0,00
|
0,00
|
1,33
|
0,00
|
|
q
|
|
|
|
|
0,5
|
|
|
2
|
0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3
|
4
|
0
|
0
|
0
|
0
|
0
|
0
|
базис
|
сi
|
bi
|
x1
|
x2
|
x3
|
x4
|
x5
|
x6
|
x7
|
x8
|
x1
|
3,00
|
1,00
|
1,00
|
0,00
|
0,00
|
0,00
|
0,00
|
0,00
|
1,00
|
-0,50
|
x2
|
4,00
|
2,00
|
0,00
|
1,00
|
0,00
|
0,00
|
0,00
|
0,00
|
-0,50
|
0,50
|
x3
|
0,00
|
1,00
|
0,00
|
0,00
|
1,00
|
0,00
|
0,00
|
0,00
|
-2,00
|
0,50
|
x6
|
0,00
|
1
|
0
|
0
|
0
|
0,666667
|
0
|
-1
|
1,666667
|
-0,5
|
x5
|
0,00
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
-1,5
|
0
|
x4
|
0,00
|
1,00
|
0,00
|
0,00
|
0,00
|
1,00
|
0,00
|
0,00
|
1,00
|
-1,50
|
|
D'
|
|
0,00
|
0,00
|
0,00
|
0,00
|
0,00
|
0,00
|
1,00
|
0,50
|
x1=1; x2=2; x3=1; x4=1; x5=1;x6=1
Ответ: x1=1; x2=2; 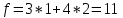
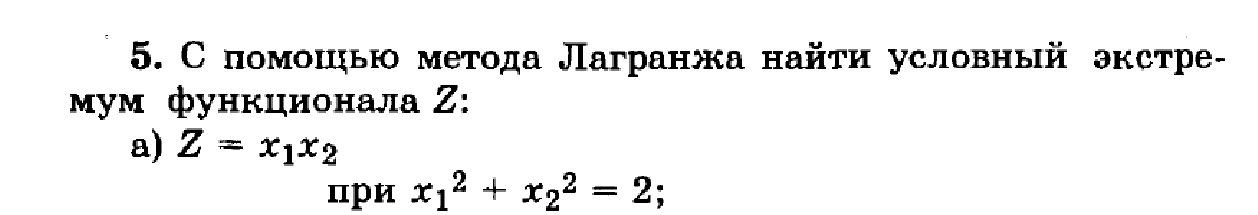
Решение
Строим функцию Лагранжа
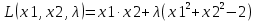
Находим частные производные
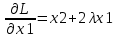 ; ;
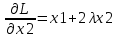 ; ;
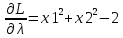 . .
Решаем систему уравнений
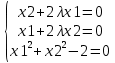 ; ;
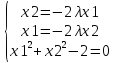 ; ; 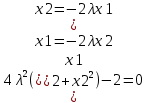 ; ; 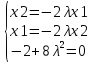 ; ; 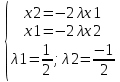 ; ;
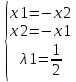 из уравнения из уравнения 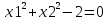 получаем получаем 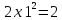 ; ; 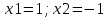 или или
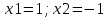
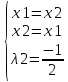 ; из уравнения ; из уравнения 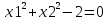 получаем получаем 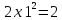 ; ; 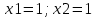 или или
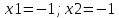
Выясним характер экстремума в каждой стационарной точке: M1(1;1), M2(−1;-1), M3(1;-1) и M4(−1;1).
Для этого вычислим определитель H в каждой из точек.
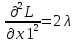 ; ; 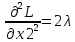 ; ; 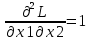 ; ;
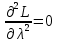 ; ; 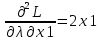 ; ;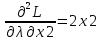 . .
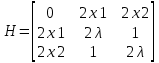
В точке M1(1;1), 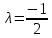
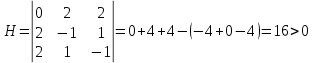
Следовательно, в точке M1(1;1) функция Z(x1,x2)=x1*x2 имеет условный максимум, Zmax=Z(1;1)=1.
В точке M2(-1;-1), 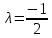
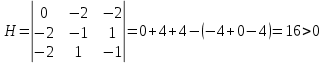
Следовательно, в точке M2(-1;-1) функция Z(x1,x2)=x1*x2 имеет условный максимум, Zmax=Z(-1;-1)=1.
В точке M3(-1;1), 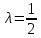
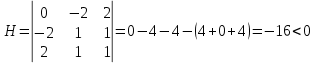
Следовательно, в точке M3(-1;1) функция Z(x1,x2)=x1*x2 имеет условный минимум, Zmin=Z(-1;1)=-1.
В точке M4(1;-1), 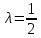
Следовательно, в точке M4(1;-1) функция Z(x1,x2)=x1*x2 имеет условный минимум, Zmin=Z(1;-1)=-1. |
 Скачать 257.42 Kb.
Скачать 257.42 Kb.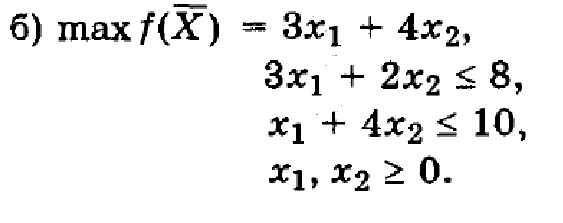

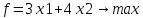
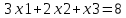
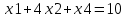
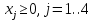
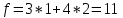
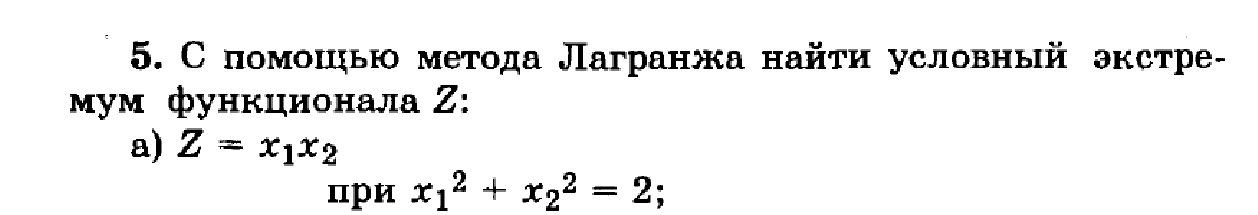
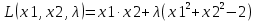
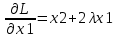 ;
;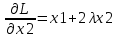 ;
;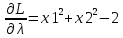 .
.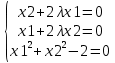 ;
;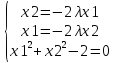 ;
; 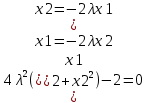 ;
; 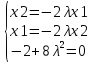 ;
; 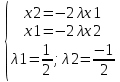 ;
;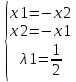 из уравнения
из уравнения 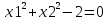 получаем
получаем 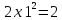 ;
; 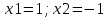 или
или 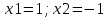
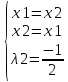 ; из уравнения
; из уравнения 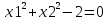 получаем
получаем 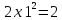 ;
; 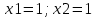 или
или 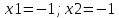
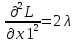 ;
; 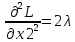 ;
; 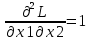 ;
;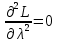 ;
; 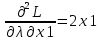 ;
;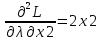 .
.