Математика 6 вариант. Решение Задание 216. Исследовать функцию на экстремум
 Скачать 288.46 Kb. Скачать 288.46 Kb.
|
|
Задание 206. Дана функция двух переменных. Найти первые и вторые частные производные: 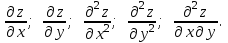 𝛕 = arcsin 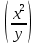 Решение: 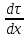 = = 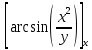 = = 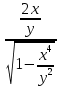 = = 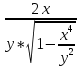 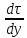 = = 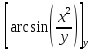 = = 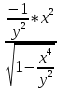 = = 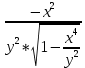 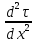 = = 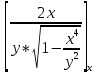 = = 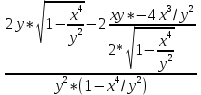 = = 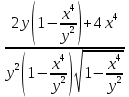 = = 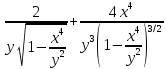 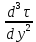 = = 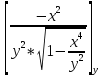 = = 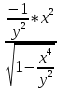 = = 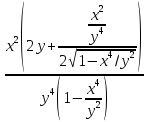 = = 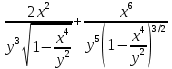 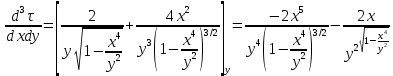 Задание 216. Исследовать функцию 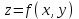 на экстремум. на экстремум.𝛕 = x2 + xy + y2 – 2x – 3y Решение: Находим частные производные I порядка: 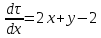 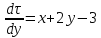 Решим систему: 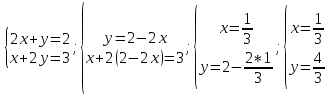 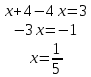 =>M 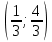 – критическая точка – критическая точка3. Находим частные производные II порядка: 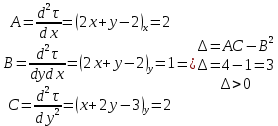 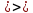 M M 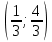 – точка min – точка minЗадание 226. Дана функция скалярного поля 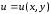 . Требуется: . Требуется:построить линии уровня 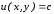 при 4-х значениях при 4-х значениях  ; ;найти производную функции  в точке в точке 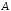 по направлению вектора по направлению вектора 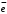 ; ;найти 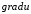 в точке в точке 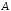 ; ;найти наибольшую скорость изменения функции в точке 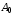 . .u = 2x2+3y2 ; A(4; -4) , ē = 2 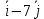 Решение: Линия уровня 2x2+3y2= C : 2x2+3y2 –c = 0 – семейство эллипсов c = 0 ; 2x2+3y2 = 0 - пара мнимых пересекающихся прямых c 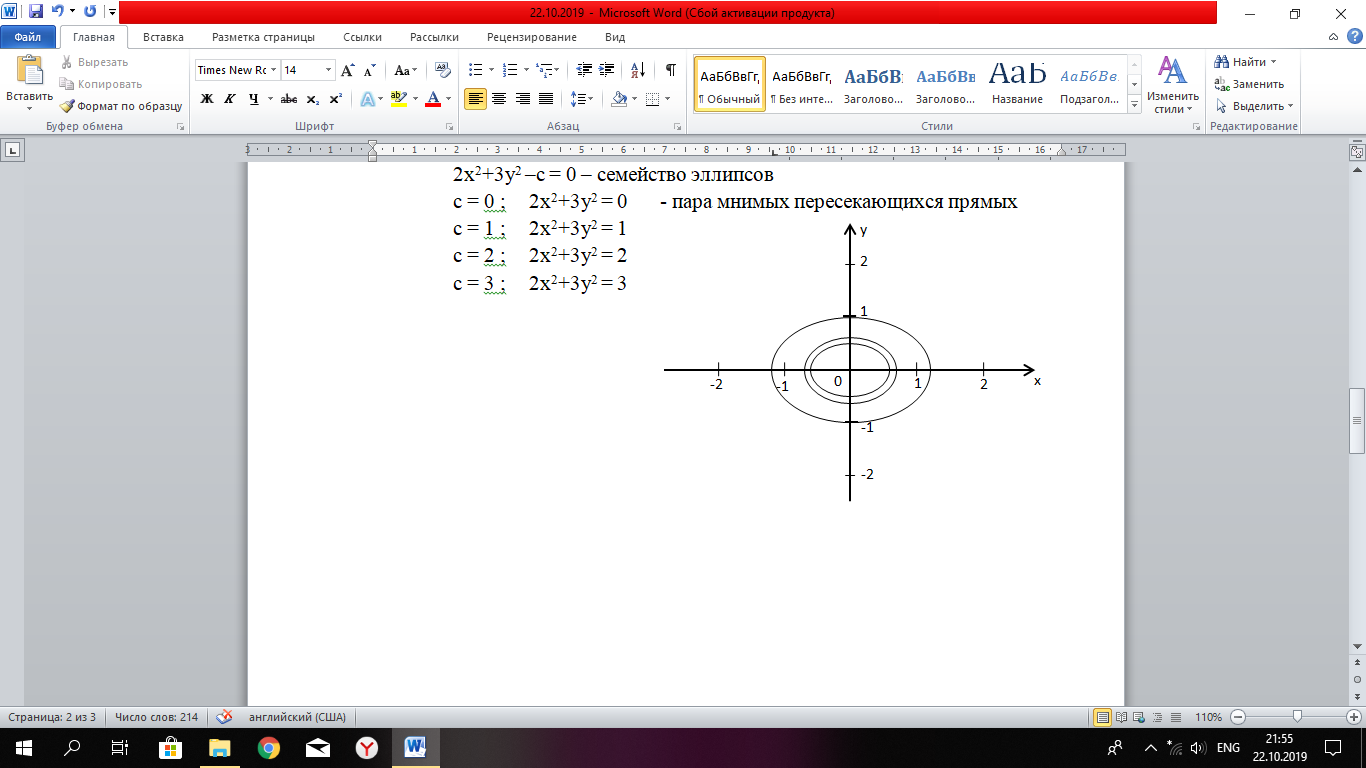 = 1 ; 2x2+3y2 = 1 = 1 ; 2x2+3y2 = 1c = 2 ; 2x2+3y2 = 2 c = 3 ; 2x2+3y2 = 3 Производная u (x;y) по направлению вектора ē = 2 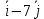 в точке А(4; - 4) в точке А(4; - 4)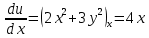 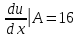 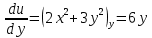 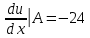 cos 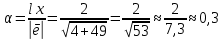 cos 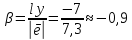 Для такого поля: 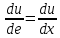 cos cos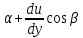 ; ;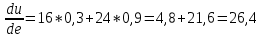 Градиент плоского поля u(x;y) gradu = 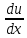 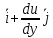 = = 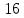 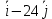 Наибольшая скорость изменения функции в точке А: 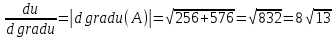 Задание 236. Прейти к полярным координатам и вычислить. 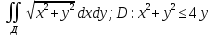  Построим область Д, ограниченную эллипсом 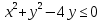 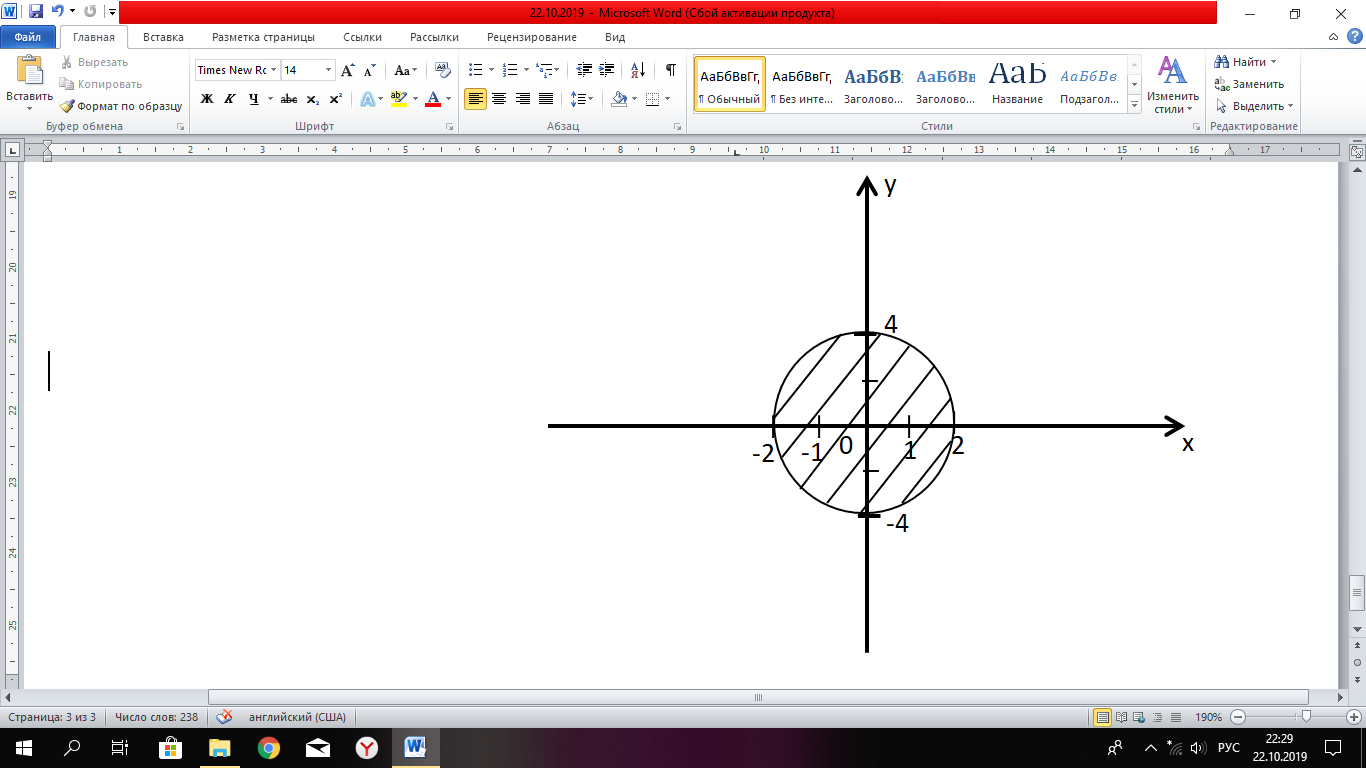 Перейдем к полярным координатам: 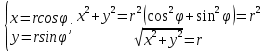 Перейдем к уравнению в полярных координатах: 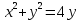 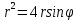 , где 0 , где 0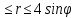 r = 4 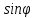 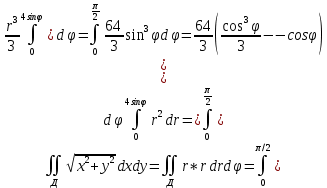 Задание 246. Найти работу силы 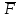 при перемещении материальной точки вдоль дуги линии при перемещении материальной точки вдоль дуги линии 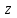 от точки от точки 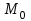 до точки до точки 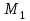 . .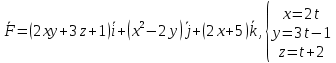 Mo (0; -1; -2) до M1 (2; 2; 3) Решение: Е = 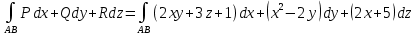 Перейдем к вычислению определенного интеграла и переменной t: 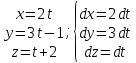 E = 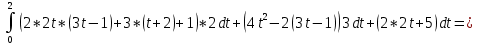 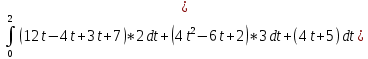 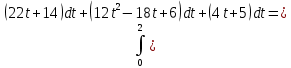 = (22* 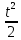 +14t) +14t)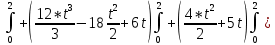 = 4*4+25*2+4*8=16+50+32=98 Задание 256. Дан числовой ряд 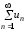 . Записать четыре первых члена ряда. Исследовать на сходимость числовой ряд. . Записать четыре первых члена ряда. Исследовать на сходимость числовой ряд.а) 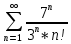 Проверим сходимость по признаку Даламбера: 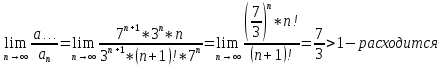 a1 = 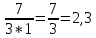 a3 = a3 = 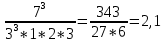 a2 = 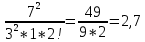 a4 = a4 = 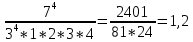 б) 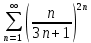 Проверим сходимость по признаку Коши: 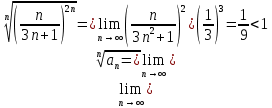 – ряд сходится a1 = 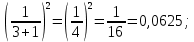 a3 = a3 = 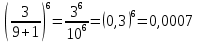 a2 = 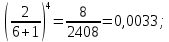 a4 = a4 = 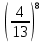 = = 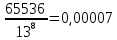 в) 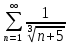 a1 = 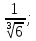 a3 = a3 =  a2 =  a4 = a4 =  Проверим интегральную сходимость:  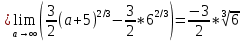 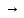 ряд сходится ряд сходится(т.к. интеграл не равен 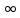 ) )Задание 266. Дан знакочередующийся числовой ряд 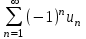 . Записать четыре первых члена ряда; Определить: условно, или абсолютно сходится этот ряд. . Записать четыре первых члена ряда; Определить: условно, или абсолютно сходится этот ряд.а) 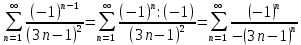 По т. Лейбница : 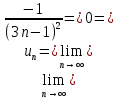 Ряд сходится a1 = 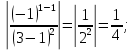 a3 = a3 = 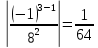 a2 = 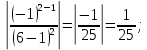 a4 = a4 = 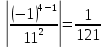 б) 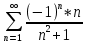 По признаку Даламбера: 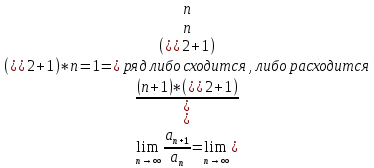 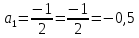 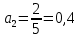 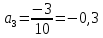 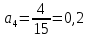 Задание 276. Определить область сходимости данного степенного ряда. Исследовать сходимость ряда на границах области. 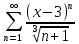 an = 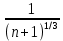 Найдем область сходимости: R = 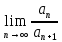 R = 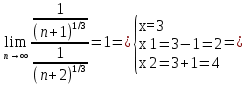 2 < R < 4 - ряд является сходящихся (абсолютно) Проверим сходимость на концах интервала 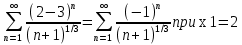 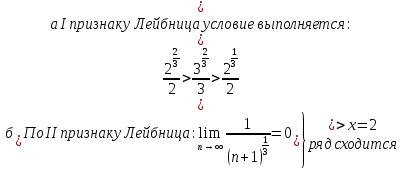 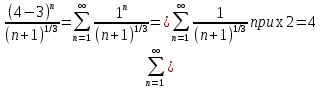 По признаку Коши: 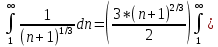 = 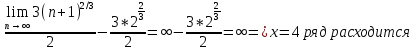 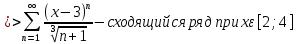 Задание 286. Вычислить определенный интеграл 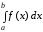 с точностью до 0,001, разложив подынтегральную функцию в ряд Маклорена и затем проинтегрировав его почленно. с точностью до 0,001, разложив подынтегральную функцию в ряд Маклорена и затем проинтегрировав его почленно.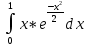 Решение: Запишем разложение функции ʄ (х)= 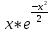 в степенной ряд в степенной рядex = 1 + x + 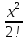 + + 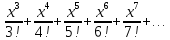 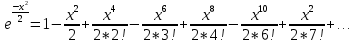 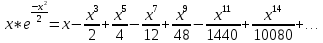 Интегрируем ряд и находим значение интеграла с точностью до 0,001. 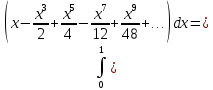 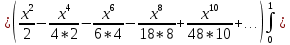 = 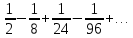 = 0,5-0,125+0,041-0,01+0,00005=0,41 = 0,5-0,125+0,041-0,01+0,00005=0,41Задание 296. Разложить данную функцию 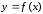 в ряд Фурье в интервале в ряд Фурье в интервале 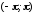 . .ʄ(х) 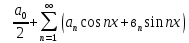 коэффициенты a0, an, вn находятся по формулам: 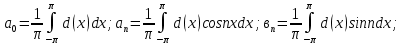 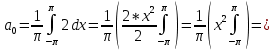 = 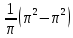 =0 =0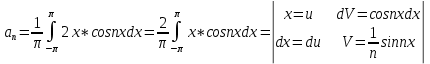 = == 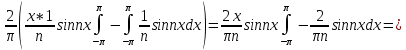 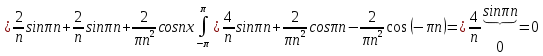 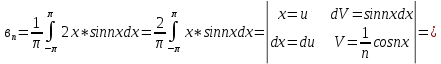 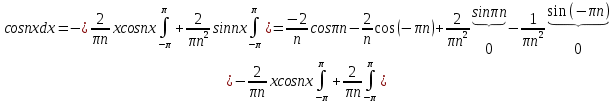 = = 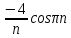 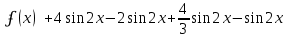 |
