контрольная работа по нефтебахам и терминалам. Решение Диаметр резервуара равен 4,73 м, высота 5,96 м. Масса нефтепродукта определяется по формуле
 Скачать 174.61 Kb. Скачать 174.61 Kb.
|
|
Задача № 1 В вертикальном цилиндрическом резервуаре типа РВС номинальной емкости V хранится М нефтепродукта плотностью 20. Определить колебание уровня нефтепродукта в резервуаре, если его температура изменилась от t1 до t2 . Расширение резервуара не учитывать. Дано: V = 100 м3; М = 70 тн 20 = 750 кг/м3; t1 = 30 0С; t2 = 00С. Найти: 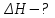 Решение: Диаметр резервуара равен 4,73 м, высота 5,96 м. Масса нефтепродукта определяется по формуле: 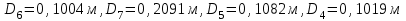 где V1, V2 – объем нефтепродукта при заданной температуре, м3; 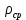 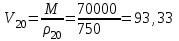 – средняя плотность нефтепродукта при заданной температуре изменения уровня, кг/м3. – средняя плотность нефтепродукта при заданной температуре изменения уровня, кг/м3.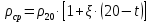 г 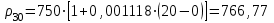 де де 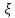 – коэффициент объемного расширения (при заданной плотности = 0,000831 1/C) – коэффициент объемного расширения (при заданной плотности = 0,000831 1/C)Изменение объема нефтепродукта при изменении температуры: 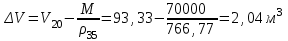 Колебание уровня нефтепродукта в резервуаре: 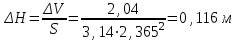 Ответ: Колебания уровня нефтепродукта в резервуаре составляет 0,116 м Задача № 3 Определить пропускную способность самотечного трубопровода диаметром Dн х мм и длиной L км при разности нивелирных отметок начальной и конечной точек трубопровода Z, м. Дано: Dн = 159 мм = 0,159 м; δ = 4 мм = 0,004 м; L = 1км = 1000 м; ΔZ = 10 м; v= 7∙10-6 м2/с; ρ20 = 850 кг/м3 Найти: Q = ? Решение: Напишем уравнение Бернулли относительно плоскости сравнения 0–0, взятой по оси симметрии трубы на выходе жидкости из трубопровода, для сечений 1–1 (уровень жидкости в резервуаре) и 2–2 (выход жидкости из трубопровода). 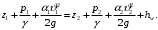 Сечения 1–1 и 2–2 выбраны потому, что давление в них известно и оно равно атмосферному рат, следовательно 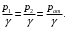 Скорость движения жидкости в резервуаре ϑ1 при достаточно больших его размерах по сравнению с выходным отверстием трубы можно считать близкой к нулю (ϑ1 ≈ 0), а значит, 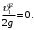 Координата сечения 1–1 над плоскостью сравнения z1= h, а сечения 2–2 z2= 0, так как плоскость сравнения 0–0 проходит по оси симметрии трубы. Принимаем α2 = 1, так как при турбулентном режиме α2 = 1,05÷1,10. С учетом выше изложенного уравнение Бернулли принимает следующий вид: 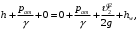 или после сокращения получаем 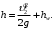 В связи с тем, что про местные потери напора в трубопроводе ничего не сказано, принимаем их равными 10% от потерь напора по длине. Тогда величину потерь напора hwопределим из выражения 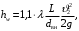 где dвн – внутренний диаметр трубы, определяемый из выражения 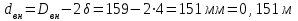 При этом коэффициент сопротивления трения, с допущением того, что данная стальная труба эксплуатируется несколько лет, приближенно принимаем равным λ = 0,02 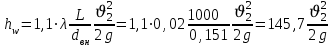 Подставив данное значение в преобразованное уравнение Бернулли, получаем: 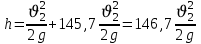 Из полученного выражения определим скорость: 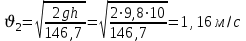 Зная скорость движения жидкости на выходе из трубы, уточним, правильно ли мы приняли λ = 0,02. Определим число Рейнольдса из выражения 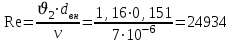 Из полученного числа Рейнольдса следует, что режим движения турбулентный. Определим, по какой формуле необходимо рассчитывать коэффициент λ. Предположив, что это переходная область турбулентного режима, произведем проверку, при этом Δэкак для бывших в употреблении бесшовных стальных труб определим из таблицы, Δэ= 0,2 мм 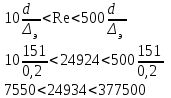 Так как неравенство выдерживается, то производим расчет коэффициента трения λ по формуле Альтшуля 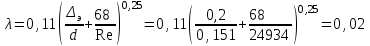 Так как коэффициенты трения λ расчетный и принятый нами полностью совпали, то уточнять скорость нет необходимости. Поэтому определяем расход из выражения 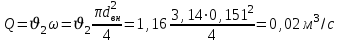 Ответ: Q = 0,02 м3 /с. Задача № 5 Определить диаметры отдельных участков разветвленного трубопровода, схема которого приводится на рис. 1. 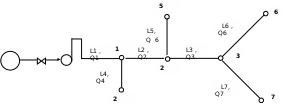 AА Рис. 1 Общее количество выкачиваемого из резервуара А нефтепродукта Q1 (м3/ч). В каждый пункт поступает Q4, Q5, Q6, Q7 (м3/ч) нефтепродукта. При производительности Q1 (м3/ч) насос развивает давлениеР1 (МПа). Давления в точках 4, 5, 6 и 7 принять равными Р2. Вязкость и плотность перекачиваемого продукта Дано:
Найти:_D_6_,_D_7_,_D_5_,_D_4_Решение'>Найти: D6, D7, D5, D4 Решение: Напор, развиваемый насосом: 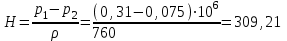 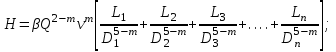 Основное расчётное уравнение: 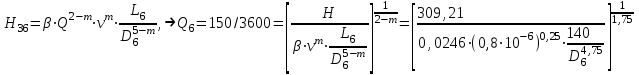 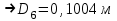 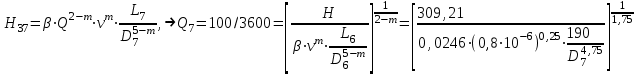 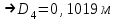 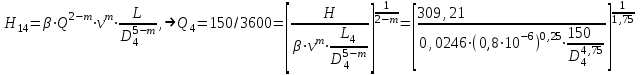 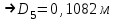 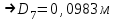 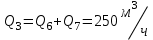 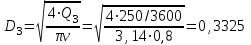 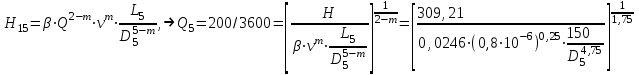 О 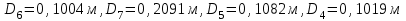 твет: твет: Задача № 7 Определить, какой должна быть температура нефтепродукта, чтобы он сливался самотеком из цистерны типа N, в течение часов. Схема слива приведена на рис. 3. Трубопровод имеет длину L, диаметр Dн мм, высоту Н. Местные сопротивления: универсальный сливной прибор, плавный переход, задвижка, два угольника. Режим движения ламинарный. Вязкость нефтепродукта 20 и 50. Дано: N = 90; = 2 ч; L = 30 м; Dн = 219х6; Н = 2 м; 20 *104 = 40 м2/с; 50*104 = 5 м2/с. Найти: t-? Решение: Габариты цистерны грузоподъемностью 90 т: длина L1=20,266 м; диаметр D1=3 м. Найдем сумму коэф. местных сопротивлений: универсальный сливной прибор – 0,73; плавный переход – 0,3; задвижка – 0,9; два угольника – 2х1,61. 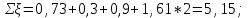 Из уравнения времени слива: 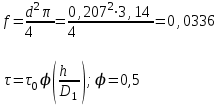 Если производится закрытый слив нефтепродуктов, необходимо ввести поправочный коэффициент 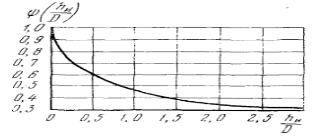 Рис. 3. График зависимости поправочного коэффициента ϕ=0,5 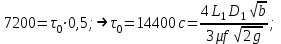 Значения b, вычисляется по формуле: 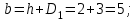 Тогда: 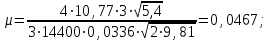 Коэф. расхода рассчитывается по формуле: 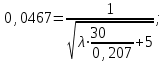 Отсюда коэф. гидравлического сопротивления: 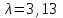 При ламинарном режиме течения число Рейнольдса равно: 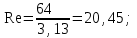 Определим скорость истечения нефти: 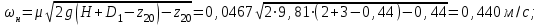 Зная число Рейнольдса и скорость истечения нефтепродукта найдем вязкость при искомой температуре: 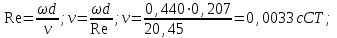 Вязкость нефти при температуре перекачке определяется по формуле 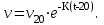  где k – эмпирический коэффициент; 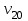 – кинематическая вязкость перекачиваемой нефти при 20С, – кинематическая вязкость перекачиваемой нефти при 20С,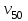 – кинематическая вязкость перекачиваемой нефти при 50С, – кинематическая вязкость перекачиваемой нефти при 50С,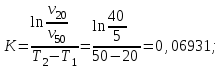 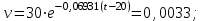 Отсюда искомая температура нефтепродукта: 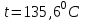 Ответ: Температура нефтепродукта= 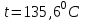 Задача № 9 Определить поверхность нагрева парового змеевикового подогревателя и расход пара для подогрева нефтепродукта в резервуаре типа РВС номинальной емкости V. В резервуаре хранится мазут марки М. Мазут хранился в резервуаре в течение времени х и был закачен в резервуар при температуре tн . Средняя температура окружающего воздуха в период хранения - tв , температура грунта - tгр , скорость ветра - Vв. Необходимая температура разогрева мазута при откачке из резервуара - tк . Время разогрева продукта в резервуаре р . Дано:
Найти: F-? Решение: Общее количество теплоты, необходимое для разогрева нефтепродукта, определяют по формуле: 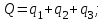 где q1 – теплота, необходимая для разогрева всей массы нефтепродукта М от начальной до конечной температуры; 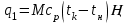 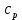 – удельная изобарная теплоемкость, Дж/(кг∙К). – удельная изобарная теплоемкость, Дж/(кг∙К).q2 – теплота, необходимая на расплавление застывшего нефтепродукта (парафина) в количестве Мп (принимаем равным нулю, так как по условию задачи нет застывшего нефтепродукта); q3 – тепловые потери в окружающую среду. 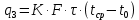 К – коэффициент теплопередачи от нефтепродукта в окружающую среду, Вт/(м2∙К); F – поверхность охлаждения, м2; τ – время разогрева; 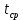 – средняя температура нефтепродукта в резервуаре за время разогрева, °С; – средняя температура нефтепродукта в резервуаре за время разогрева, °С;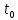 – температура окружающей среды, °С. – температура окружающей среды, °С.Удельная массовая теплоемкость для нефтепродуктов лежит в пределах 1600–2500 Дж/(кг∙К). Для расчетов принимаем среднее значение, равное 2100 Дж/(кг∙К). 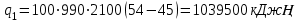 Коэффициент теплопередачи К рассчитывают в зависимости от типа емкости, толщины стенок, изоляции, способов хранения (наземный, подземный), а также принимают по опытным или справочным данным. При расчетах коэффициент К для стенок наземных металлических резервуаров принимают равным 5 – 7 Вт/(м2∙К). Примем коэффициент К для стенок равным 6 Вт/(м2∙К), для днища равным 0,3 Вт/(м2∙К), для крыши равным 1 Вт/(м2∙К). Технические характеристики РВС-100: диаметр – 10,43 м, высота - 9 м, площадь днища 42,69 м2, площадь стенки – 340 м2. Определим эффективную температуру с учетом охлаждающего эффекта ветра: 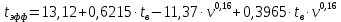 где 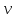 – скорость ветра, м/с. – скорость ветра, м/с.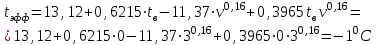 Найдем тепловые потери в окружающую среду для днища, стенок и крыши РВС: 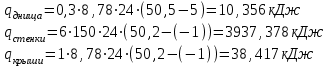 Тогда общее количество теплоты, необходимое для разогрева нефтепродукта: 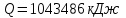 Мощность парового нагревателя за один час: 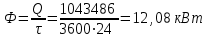 Нагрев мазута производится паром. На входе в нагреватель температуру насыщения пара принимаем t1 = 130 °С. Степень сухости насыщенного пара x = 0,9. На выходе из нагревателя пар конденсируется, его температуру принимаемt2 = 100 оС. Определим энтальпию влажного насыщенного пара 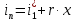 где 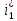 - энтальпия кипящей жидкости при насыщенииtн = 130 °С, равна 546,3 кДж/кг; - энтальпия кипящей жидкости при насыщенииtн = 130 °С, равна 546,3 кДж/кг;r – теплота парообразования при tн = 130 оС, равна 2174,4 кДж/кг. 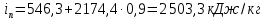 Энтальпия конденсата: 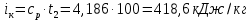 Определим требуемый расход пара: 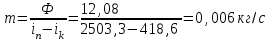 Площадь поверхности нагрева теплообменника найдем по формуле: 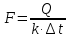 где 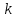 - коэффициент теплопередачи теплообменника, примем k=3,4 кВт/(м2C). - коэффициент теплопередачи теплообменника, примем k=3,4 кВт/(м2C).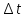 – среднелогарифмический температурный напор: – среднелогарифмический температурный напор: 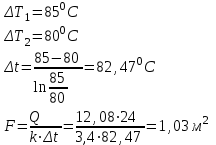 Ответ: Площадь поверхности нагрева равна 1,03 м2, требуемый расход пара = 0,006кг/с. Задача № 11 Определить потери автобензина за одно «малое дыхание» в июле из резервуара типа РВС номинальной емкости V, расположенного в местности с географической широтой . Высота взлива нефтепродукта в резервуаре Hвзл . Максимальная температура воздуха – tв max, минимальная температура воздуха – tв min ,продолжительность дня - . Нагрузка дыхательных клапанов – Рк.д. и Рк.в. Барометрическое давление – Ра. Температура начала кипения бензина – tн.к. Плотность бензина - 20. Определить на какое давление должен быть установлен дыхательный клапан, чтобы при условиях данной задачи потери от «малых дыханий» были равны нулю. Дано:
Найти: G м.б.-? Решение: Резервуар –1000 м3 степень заполнения резервуара –0,4 среднее атмосферное давление: Ра =100000 Па давление насыщенных паров по Рейду: Рру =56000 Па Принимая Р1 ≈ Р2 ≈ Ра: 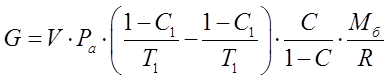 Находим упругость паров Ру соответственно температуре верхних слоев бензина ( при tв.с.п.min и tв.с.п.max): Ру1 =0,33 атм Ру2 = 0,55 атм С1 = Ру1/Ра=0,33/1=0,33 С2 = Ру2/Ра=0,55/1=0,55 Определяем среднюю объемную конденсацию паров бензина: С=(С1+С2)/2=(0,33+0,55)/2=0,44 Определяем среднюю объемную конденсацию паров бензина: Мб = 60 + 0,3tн.к. + 0,001t2н.к.= 60+0,3·50+0,001·502=77,5 кг/моль Объем газового пространства: V=400 м3 абсолютные температуры газового пространства: Т1 =T+Trmin=273+17=290К Т2=T+trmax= 273+35=308 К Подставляя значения в формулу, определим потери бензина за одно малое "дыхание": 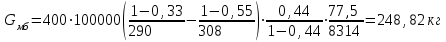 Ответ: потери автобензина за одно "малое дыхание" 248,82 кг |
