математика к.р.1, вариант 9. К. р. 1. Вариант 9. Решение 1 Формулы Крамера,, где основной определитель системы
 Скачать 0.73 Mb. Скачать 0.73 Mb.
|
|
| φ | 0 | | | | | | | | |
| r | 0,33 | 0,34 | 0,36 | 0,41 | 0,5 | 0,61 | 0,77 | 0,92 | 1 |
| φ | | | | | | | | | |
| r | 0,92 | 0,77 | 0,61 | 0,5 | 0,41 | 0,36 | 0,34 | 0,33 | |
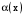 при
при 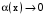 .
.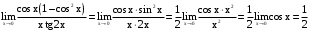 .
.По правилу Лопиталя
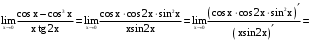
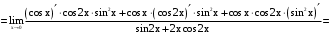
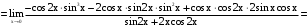
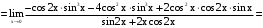
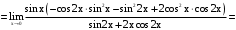
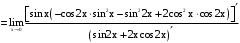 .
.Найдем отдельно пределы числителя и знаменателя (из-за длины), а затем их отношение.
Предел числителя
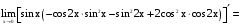
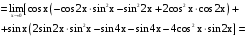
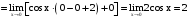 .
.Предел знаменателя
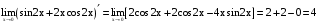 .
.Ответ:
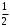 .
. г)
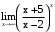 . Неопределенность
. Неопределенность 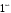 .
.Преобразуем выражение и применим 2 – й замечательный предел
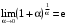 .
.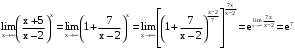 .
.Ответ: а)
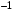 , б)
, б) 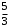 , в)
, в) 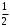 , г)
, г) 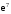 .
.51 – 60. Задана функция
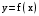 . Найти точки разрыва функции, если они существуют. Сделать чертеж.
. Найти точки разрыва функции, если они существуют. Сделать чертеж.59.
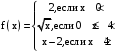 .
.Решение
Элементарные функции 2,
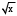 и
и 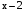 непрерывны на заданных промежутках, поэтому точки разрыва функции
непрерывны на заданных промежутках, поэтому точки разрыва функции 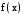 следует искать среди тех точек, в которых меняется её аналитическое задание, т.е. точек 0 и 4.
следует искать среди тех точек, в которых меняется её аналитическое задание, т.е. точек 0 и 4.Функция непрерывна в точке, если она определена в ней, и её левый и правый пределы равны значению функции в этой точке.
Находим пределы функции слева и справа от этих точек.
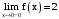 .
.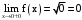 .
.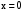 – точка разрыва 1 рода (скачок).
– точка разрыва 1 рода (скачок).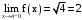 .
.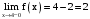 .
.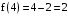 .
.В точке
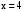 функция непрерывна.
функция непрерывна.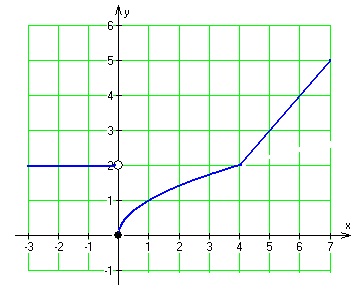
Ответ:
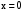 – точка разрыва 1 рода (скачок равен 2).
– точка разрыва 1 рода (скачок равен 2).61 – 70. Найти производные
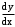 данных функций.
данных функций.Решение
69. а)
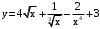 .
.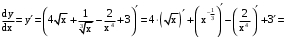
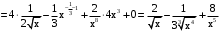 .
.Применены формулы дифференцирования:
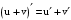 ,
, 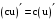 ,
, 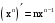 ,
, 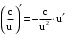 .
.Ответ:
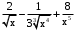 .
.б)
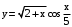 .
.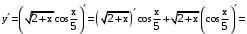
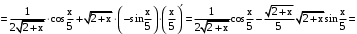
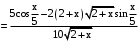 .
.По формулам:
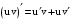 ,
, 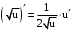 ,
, 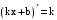 ,
, 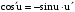
Ответ:
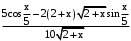 .
.в)
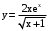 .
.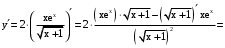
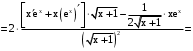
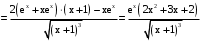 .
.По формулам:
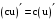 ,
, 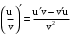 ,
, 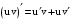 ,
, 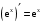 ,
, 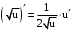 .
.Ответ:
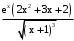 .
.г)
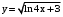 .
.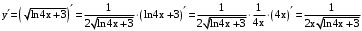
По формулам:
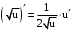 ,
, 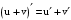 ,
, 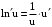
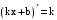
Ответ:
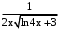 .
.71 – 80. Найти производную
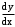 показательно-степенной функции.
показательно-степенной функции.79.
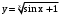 .
.Решение
Переменная х содержится и в основании и в показателе степени.
Сначала логарифмируем обе части равенства.
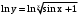 .
.По свойству логарифма степени получим
 .
.Дифференцируем обе части равенства.
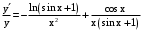 .
.Отсюда выражаем
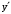 .
. 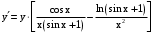 .
.Ответ:
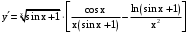 .
.81–90. Исследовать данную функцию методом дифференциального исчисления и построить её график.
89.
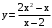 .
.Решение
Функция общего вида.
Область определения функции
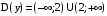 .
.Нули функции:
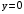 при
при 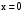 и
и 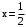 .
.Промежутки знакопостоянства
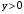 при
при 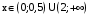 .
.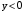 при
при 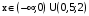 .
.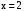 – точка разрыва.
– точка разрыва. Асимптоты.
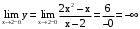 .
.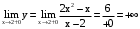 .
.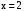 – вертикальная асимптота.
– вертикальная асимптота.Ищем наклонную асимптоту
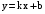 .
.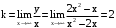 .
.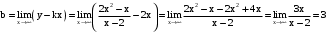 .
.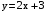 – наклонная асимптота.
– наклонная асимптота.Промежутки монотонности и экстремумы.
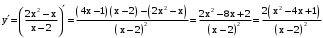 .
.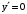 , если
, если 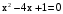 , т.е. при
, т.е. при 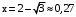 и и
и и 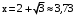 .
.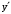 не существует при
не существует при 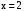 .
.Знаки производной и поведение функции
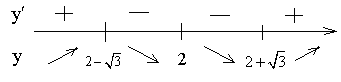
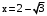 – точка максимума.
– точка максимума. Максимум равен
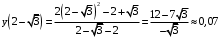 .
.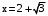 – точка минимума.
– точка минимума.Минимум равен
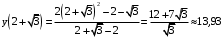 .
.Выпуклости, перегибы.
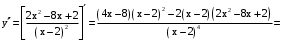
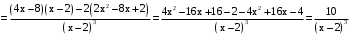
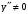 .
.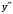 не существует при
не существует при 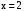 .
.Знаки второй производной и направления выпуклости
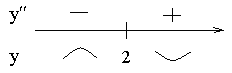
Перегибов нет.
График функции
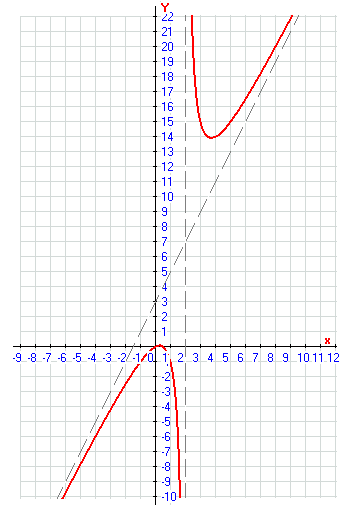
Ответ:
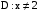 , функция возрастает на
, функция возрастает на 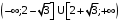 , убывает на
, убывает на 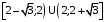 ,
, 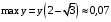 ,
, 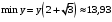 , имеет асимптоты
, имеет асимптоты 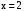 и
и 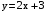 , перегибов нет.
, перегибов нет.91 –100. Найти частные производные функции
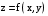 . Показать, что
. Показать, что 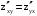 .
.99.
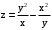 .
.Решение
Производную по каждой переменной находим, считая другую переменную постоянной величиной.
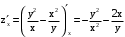 .
.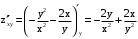 .
.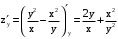 .
.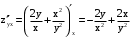 .
.Ответ: равенство
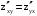 выполняется.
выполняется.101 –110. Найти наименьшее и наибольшее значения функции
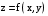 в замкнутой области.
в замкнутой области.109.
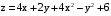 ,
, 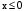 ,
, 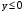 ,
, 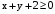 .
.Решение
Свое наибольшее (наименьшее) значение в заданной области функция может принимать либо во внутренней точке области, либо на границе области. Если внутри области имеются точки экстремума, то в этих точках обе частные производные функции равны 0, или не существуют.
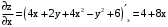 .
. 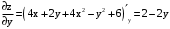 .
. 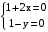 ,
, 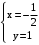 .
. Точка
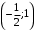 не принадлежит заданной области.
не принадлежит заданной области.Внутри области точек экстремума нет.
Исследуем границы области. На каждом участке границы функция может принимать наибольшее (наименьшее) значение либо в критической точке, принадлежащей этому участку, либо на конце участка.
На OA:
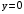 ,
, 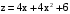 ,
, 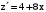 ,
, 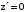 при
при 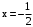 . Точка
. Точка 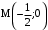 .
.На OB:
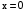 ,
, 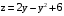 ,
, 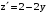 ,
, 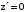 при
при 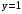 . Точка
. Точка 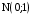
На AB:
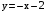 ,
, 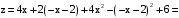
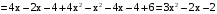 ,
,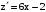 ,
, 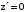 при
при 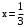 ,
, 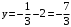 .
. Точка
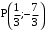 не принадлежит заданной области.
не принадлежит заданной области.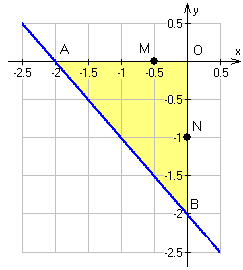
Находим значения функции в точках
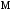 и
и 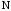 , и из полученных чисел выбираем наибольшее и наименьшее.
, и из полученных чисел выбираем наибольшее и наименьшее.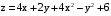 .
.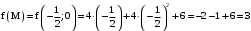 .
.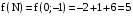 .
.Ответ:
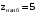 ,
, 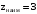 .
.111 –120. Экспериментально получено 5 значений искомой функции
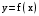 при пяти значениях аргумента, которые записаны в таблице.
при пяти значениях аргумента, которые записаны в таблице.Методом наименьших квадратов найти функцию
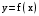 в виде
в виде 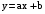 .
. 119.
| х | 1 | 2 | 3 | 4 | 5 |
| у | 5,7 | 6,7 | 5,2 | 3,2 | 3,7 |
Решение
Методом наименьших квадратов коэффициенты aи b находим из системы уравнений
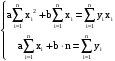 .
. 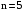 .
.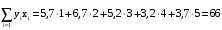 .
.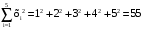 .
.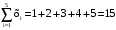 .
.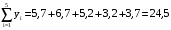 .
.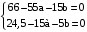 ,
, 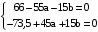 ,
, 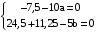 ,
, 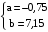 .
.Ответ:
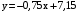 .
.
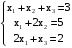
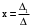 ,
, 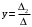 ,
, 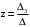 где:
где: 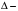
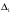 – определитель, полученный из основного заменой
– определитель, полученный из основного заменой 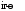 столбца на столбец свободных членов.
столбца на столбец свободных членов.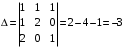 .
.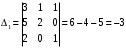 .
.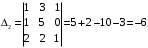 .
.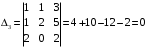 .
.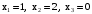 .
.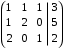 .
.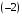 . 3 строку заменим суммой с 1 – й.
. 3 строку заменим суммой с 1 – й.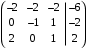
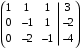 .
.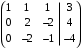
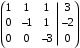 .
.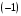 и на
и на 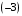 .
.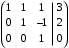 .
.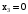 ,
,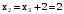 .
.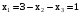 .
.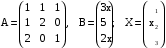 .
.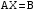 . Умножим обе части этого равенства на матрицу
. Умножим обе части этого равенства на матрицу 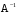 , обратную матрице A.
, обратную матрице A. 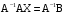 .
.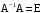 , где E - единичная матрица, получим
, где E - единичная матрица, получим 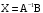 .
.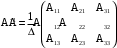 , где
, где 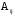 – взятый со знаком
– взятый со знаком 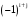 определитель 2-го порядка, полученный из определителя матрицы A вычеркиванием
определитель 2-го порядка, полученный из определителя матрицы A вычеркиванием 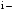 й строки и
й строки и 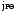 столбца.
столбца.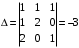 .
.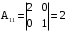 ,
, 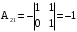 ,
, 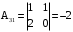 ,
,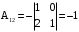 ,
, 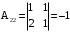 ,
, 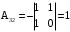 ,
,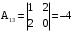 ,
, 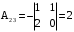 ,
, 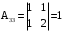 .
.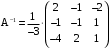 .
.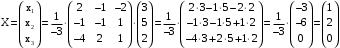
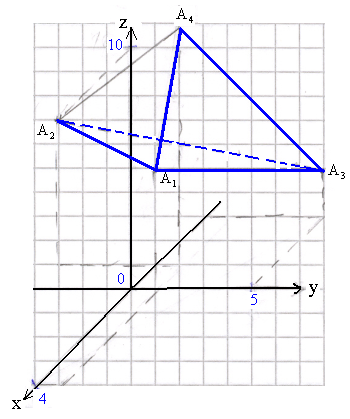
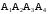 . Требуется:
. Требуется: 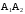 ;
; 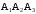 .
.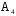 на грань
на грань 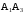 ;
;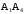 и гранью
и гранью 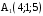 ,
, 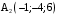 ,
, 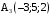 ,
, 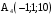 .
.
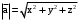 .
.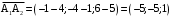 .
.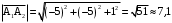 .
.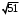 .
.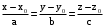 уравнений прямой, проходящей через данную точку
уравнений прямой, проходящей через данную точку 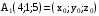 с данным направляющим вектором
с данным направляющим вектором 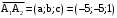 .
.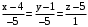 .
.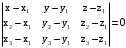 .
. 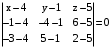 .
. 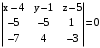 .
.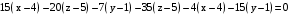 .
.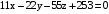 .
.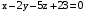 .
.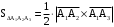 .
.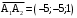 .
.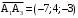 .
.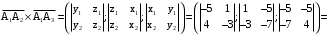
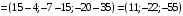 .
.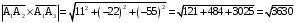 .
.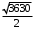 кв. ед.
кв. ед.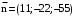 к плоскости
к плоскости 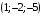 .
.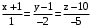 - уравнения высоты.
- уравнения высоты.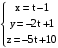 .
. 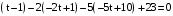 .
. 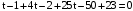 .
.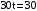 ,
,  .
. 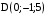 .
.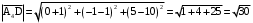 .
. .
.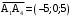 .
.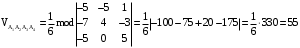 .
.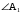 между ребрами найдем, используя формулу косинуса угла между векторами
между ребрами найдем, используя формулу косинуса угла между векторами 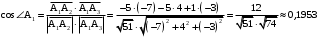 .
.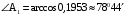 .
.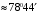 .
.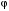 между ребром
между ребром 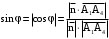 , где
, где 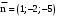 - вектор нормали к грани
- вектор нормали к грани 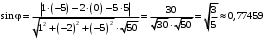 .
.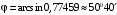 .
.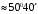 .
.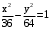 .
.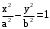 .
.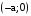 ,
, 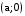 .
.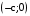 ,
, 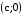 , где
, где 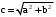 .
.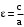 .
.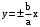 .
.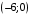 ,
, 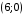 ; фокусы
; фокусы 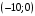 ,
, 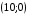 ; эксцентриситет
; эксцентриситет 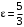 ; асимптоты
; асимптоты 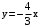 и
и 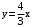 .
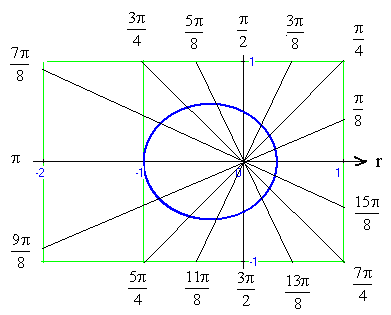
.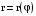 в полярной системе координат.
в полярной системе координат.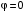 до
до 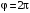 , придавая
, придавая 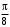 ;
;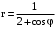
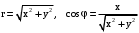 . Подставим в (1).
. Подставим в (1).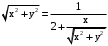 .
. 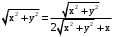 .
. 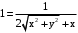 .
.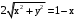 . Возведем в квадрат.
. Возведем в квадрат.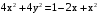 .
.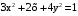 .
.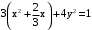 .
.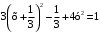 .
. 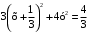 . Разделим уравнение на
. Разделим уравнение на 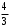 .
.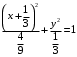 . Эллипс с центром симметрии в точке
. Эллипс с центром симметрии в точке 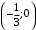 .
.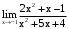 .
.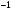 вместо х получим неопределенность
вместо х получим неопределенность 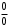 .
.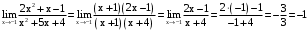 .
.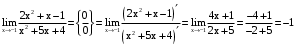 .
.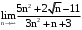 . Неопределенность
. Неопределенность 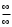 . Делим числитель и знаменатель на наибольшую степень n.
. Делим числитель и знаменатель на наибольшую степень n.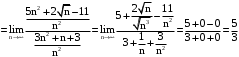 .
.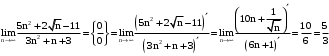 .
.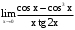 . Неопределенность
. Неопределенность 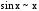 при
при 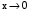 ,
,