Решение. 1 Проводим проверку гипотезы о равенстве дисперсий h 0 d x d y
 Скачать 29.21 Kb. Скачать 29.21 Kb.
|
|
Практическая работа 4 Для сравнения двух марок стали А и В с точки зрения их предела текучести проверяется 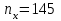 проб стали марки А и проб стали марки А и 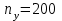 проб стали марки В. Получены следующие статистические характеристики: для марки А: проб стали марки В. Получены следующие статистические характеристики: для марки А: 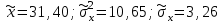 ; для марки В: ; для марки В:  . Считая распределения величин Х и Y нормальным, проверить при уровне значимости . Считая распределения величин Х и Y нормальным, проверить при уровне значимости  : 1) гипотезу о равенстве дисперсий : 1) гипотезу о равенстве дисперсий  ; 2) гипотезу о равенстве математических ожиданий ; 2) гипотезу о равенстве математических ожиданий 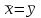 . .Решение. 1) Проводим проверку гипотезы о равенстве дисперсий: H0: Dx = Dy; Альтернативная гипотеза: H1: Dx ≠ Dy; Найдём наблюдаемое значение критерия Фишера:  . .Числа степеней свободы: f1 = nу – 1 = 200 – 1 = 199 f2 = nx – 1 = 145 – 1 = 144 По таблице критических точек распределения Фишера–Снедекора при уровне значимости α = 0.05 и данным числам степеней свободы находим Fкр(199;144) = 1,27. Т.к. Fнабл < Fкр, то нет оснований отвергать нулевую гипотезу (т.е. можно считать, что дисперсии двух выборок равны). 2) 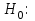 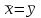  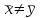 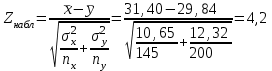  Так как 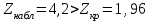 то нулевую гипотезу следует отвергнуть в пользу альтернативных. Средние двух выборок не равны. то нулевую гипотезу следует отвергнуть в пользу альтернативных. Средние двух выборок не равны. |
