Решение. Решение 1) Внутри обоих цилиндров (
 Скачать 106.98 Kb. Скачать 106.98 Kb.
|
|
Задача3. Найти потенциал незаряженного проводящего шара, на расстоянии r от центра которого расположен точечный заряд q. Решение: Применим теорему Гаусса. Выберем в качестве замкнутой поверхности концентрическую сферу радиуса r > R (рис.). Очевидно, что напряженность на поверхности этой сферы будет одинакова по величине и направлена по радиусу. Тогда поток напряженности через нее будет E ⋅ 4πr2. Согласно теореме Гаусса откуда Выбрав в качестве поверхности сферу радиуса r < R, получим E = 0. Таким образом, однородно заряженная сфера во внешней области пространства создает такое же поле, как и заряд, помещенный в ее центре. Внутри сферы поля нет. Найдем потенциал сферы во всем пространстве. Так как вне сферы напряженность поля совпадает с напряженностью заряда, находящегося в центре, то и потенциал при r > R выразится в виде Пронесем единичный положительный заряд из бесконечности до расстояния r от центра, меньшего радиуса сферы. Тогда работа, которую необходимо совершить по переносу до поверхности сферы будет равна kq∕R. Внутри сферы поле равно нулю и работа не совершается. Таким образом Ответ: Задача 10. Имеются два бесконечно длинных коаксиальных металлических цилиндра с радиусами a = 2 см и b = 5 см. Пространство между цилиндрами заполнено воздухом. Потенциал внутреннего цилиндраa =5В,внешний цилиндр заземлён. Найти распределение потенциала в пространстве между цилиндрами. Вычислит значение потенциала на окружности радиусом = 4 см Решение: 1) Внутри обоих цилиндров (r < R1) результирующая напряженность поля Е = 0; электрическое смещение D = εε0Е = 0. 2) Между цилиндрами результирующая напряженность поля: в области без диэлектрика (R1 ≤ r ≤ R0) 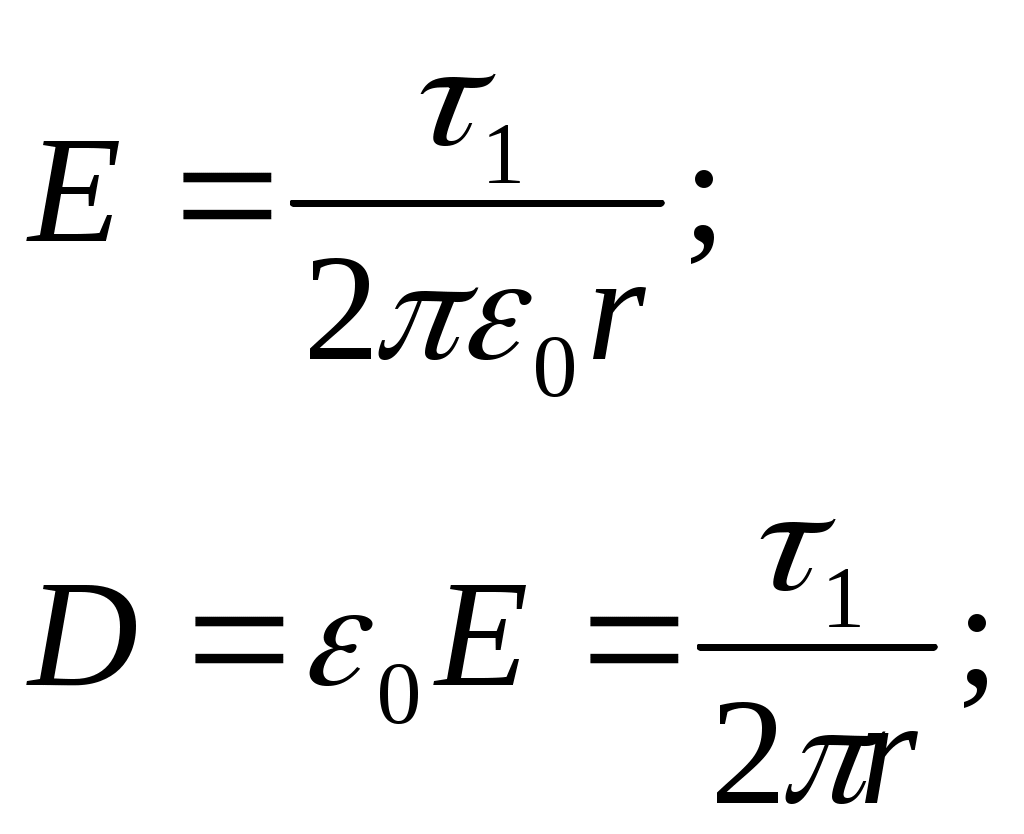 в области с диэлектриком (R0 < r ≤ R2) 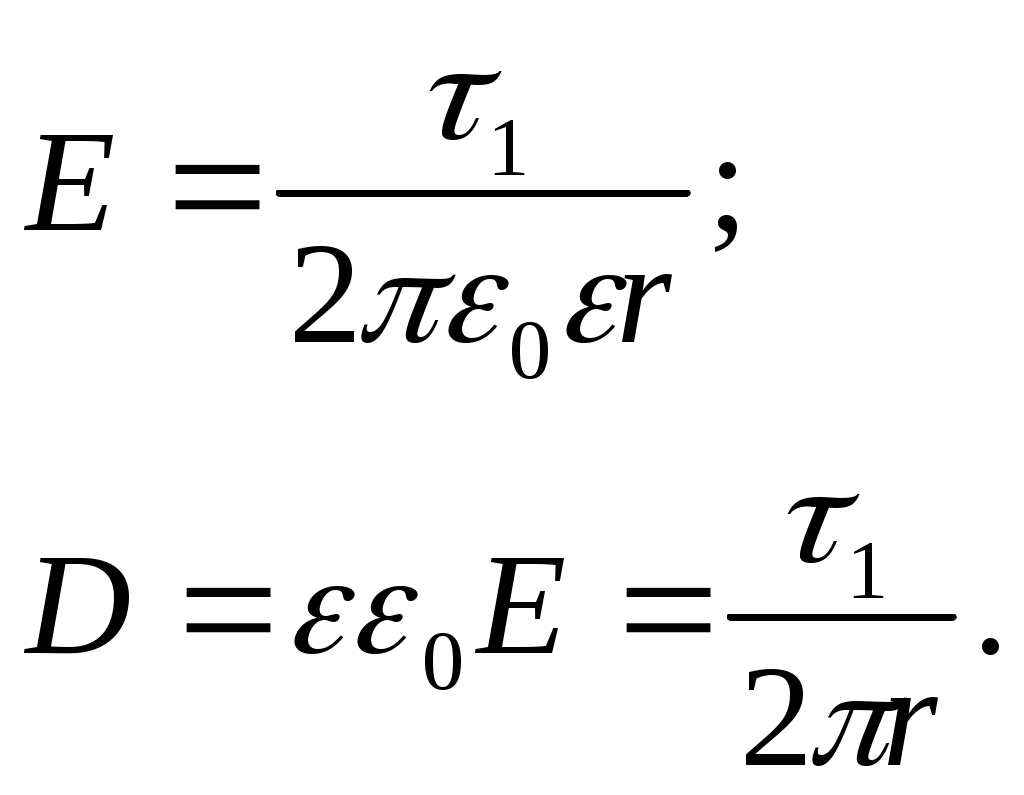 3) Вне цилиндров (r > R2) 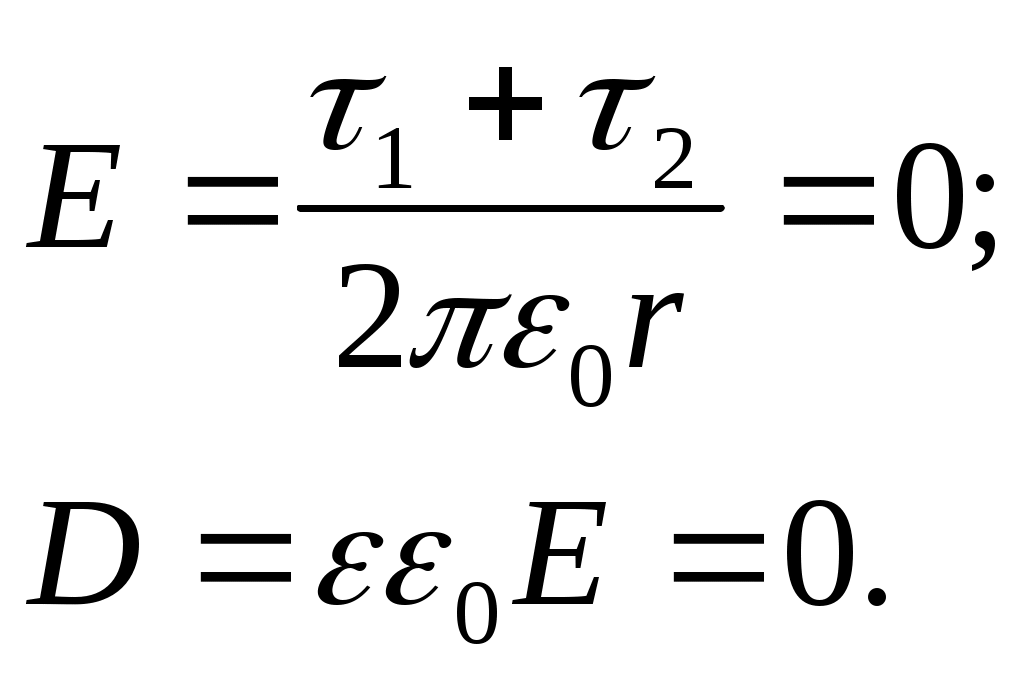 Найдем разность потенциалов между точками r1 = 2 см и r2 = 5 см по формуле 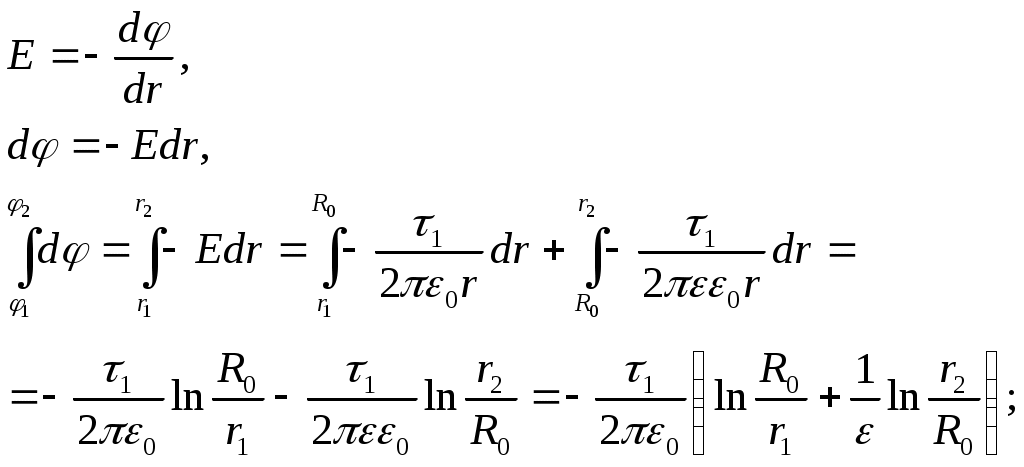 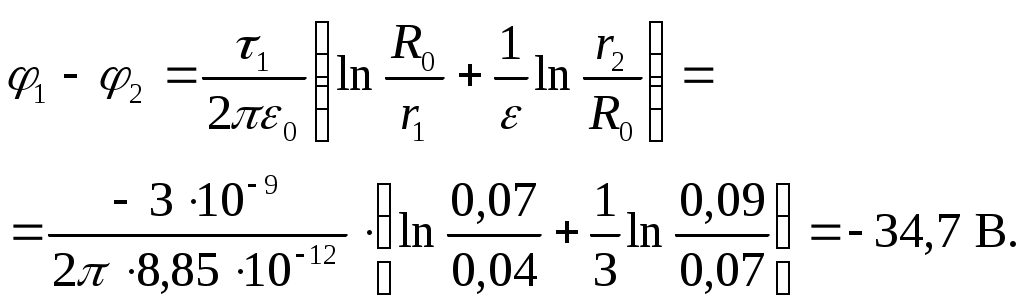 Ответ: φ1–φ2 = –34,7 В. Задача 11. Внутри сферической области радиуса a равномерно распределён заряд с объёмной плотностью ρ. Предполагая, что относительные диэлектрические проницаемости внутренней и внешней областей равны единице, определить напряжённость и потенциал в обеих областях. Решение: Объёмную плотность энергии шара определим по формуле: ρ=qV(1),V=43⋅π⋅R3(2),q=ρ⋅43⋅π⋅R3 Так как точечный заряд, расположенный на поверхности, а внутри поля нет Напряженность поля шара, вычисленная с помощью теоремы Остроградского Гаусса : E=q⋅r4⋅π⋅ε⋅ε0⋅R3=ρ⋅r3⋅ε⋅ε0,(r<R),E=q4⋅π⋅ε⋅ε0⋅R2,(r=R),E=q4⋅π⋅ε0⋅r2=k⋅qr2,(r>R) 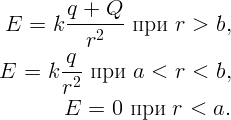 Для потенциала при r > b имеем φ = k(q + Q)∕r. На поверхности внешней сферы φ(b) = k(q + Q)∕b. Так как эта сфера заземлена, φ(b) = 0. Отсюда Тогда напряженность поля при r > b равна нулю. Вне заземленной сферы поля нет. Этот результат не зависит от формы заземленного проводника. Говорят, что заземленная оболочка экранирует находящиеся внутри заряды: никакие изменения их величины или положения не сказываются снаружи. Понятно, что при r > b потенциал равен нулю. Для нахождения потенциала между сферами пронесем единичный положительный заряд из бесконечности в данную точку, используя принцип суперпозиции. В поле заряда Q работа совершается лишь до поверхности внешней сферы: φ1 = kQ∕b--kq∕b. А в поле внутренней сферы φ2 = kq∕r. Полный потенциал E = 0, потенциал не меняется и равен потенциалу на поверхности |
