Решение 1

Название	Решение 1
Дата	15.07.2020
Размер	240.4 Kb.
Формат файла
Имя файла	61.docx
Тип	Решение #134425

Задача 1

В электрической цепи (рис. 1) в результате коммутации возникает переходный процесс. Параметры цепи для каждого варианта приведены в табл. 1, постоянное напряжение источника питания 100 В, сопротивления резисторов в схемах рис. 1 одинаковы.

Необходимо:

1. Определить начальные значения токов в ветвях и напряжения на конденсаторе (если он есть) до коммутации и в первый момент после коммутации.

2. Определить принужденные значения токов в ветвях и напряжения на конденсаторе (если он есть).

3. Определить постоянную времени цепи.

4. Построить графики изменения во времени токов в ветвях и напряжения на конденсаторе (если он есть) на основе начальных и принужденных значений

Дано: E = 100 В; r = 10 Ом; C = 150 мкФ.

Решение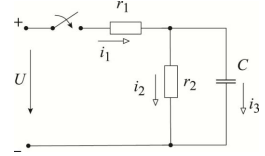

1. Расчет режима до коммутации

Токи в ветвях цепи

i₁(0–) = i₂(0–) = i₃(0–) = 0.

По второму закону коммутации

u_C(0) = u_C(0–) = 0 В.

2. Расчет принужденного режима после коммутации

Токи в ветвях цепи

i_1пр = i_2пр = = = 5 А,

i_3пр = 0.

Напряжение на конденсаторе

u_C_пр = i_1прr = 5∙10 = 50 В.

3. Расчет коммутационного режима

Уравнения по законам Кирхгофа для схемы после коммутации

i₁ – i₂ – i₃ = 0,

i₁r + i₂r= E,

i₂r – u_C = 0.

Для момента времени t = 0

i₁(0) – i₂(0) – i₃(0) = 0,

i₁(0)r + i₂(0)r= E,

i₂(0)r – u_C(0) = 0,
i₁(0) – i₂(0) – i₃(0) = 0,

i₁(0) + i₂(0) = ,

i₂(0) = ,
Токи в активных ветвях цепи

i₁(0) = = = 10 А,

i₂(0) = = 0;

i₃(0) = i₁(0) – i₂(0) = 10 – 0 = 10 А.
4. Определение корней характеристического уравнения

Комплексное сопротивление ветви с емкостью

Z₃(j) = .

Комплексное сопротивление разветвления

Z₂₃(j) = = .

Комплексное сопротивление цепи

Z(j) = r₁ + Z₂₃(j) = r₁ +

Характеристическое уравнение при j = p с учетом r₁ = r₂ = r₃ = r

Z(p) = r + = 0,

rpC + 2 = 0.

Корень характеристического уравнения

p = – = – = – 1333 с^-1.

5. Определение постоянных интегрирования и законов изменения токов

Свободные составляющие токов ветвей и напряжения на конденсаторе

i₁_св(t) = A₁e^–¹³³³^t;

i₂_св(t) = A₂e^–¹³³³^t;

i₃_св(t) = A₃e^–¹³³³^t ;

u_C_св(t) = Be^–¹³³³^t.

Законы изменения токов ветвей

i₁(t) = i_1пр + i_1св(t) = 5 + A₁e^–¹³³³^t А,

i₂(t) = i_2пр + i_2св(t) = 5 + A₂e^–¹³³³^t А,

i₃(t) = i_3пр + i_3св(t) = 0 + A₃e^–¹³³³^t А.

Закон изменения напряжения на конденсаторе

u_C(t) = u_C_пр + u_C_св(t) = 50 + Be^–¹³³³^t В .

Для момента времени t = 0

i₁(0) = 5 + A₁ = 10,

i₂(0) = 5 + A₂ = 0,

i₃(0) = 0 + A₃ = 10,

u_C(0) = 50 + B = 0.

Постоянные интегрирования

A₁ = 10 – 5 = 5 А,

A₂ = 0 – 5 = – 5 А,

A₃ = 10 – 0 = 10 А,

B = 0 – 50 = – 50 В.

Токи ветвей переходного режима

i₁(t) = i₁_пр + i₁_св(t) = 5 + 5e^–¹³³³^t А,

i₂(t) = i₂_пр + i₂_св(t) = 5 – 5e^–¹³³³^t А,

i₃(t) = i₃_пр + i₃_св(t) = 10e^–¹³³³^t А.

Переходное напряжение на конденсаторе
u_C(t) = u_C_пр + u_C_св(t) = 50 – 50e^–¹³³³^t В.
Графики найденных токов и напряжения на конденсаторе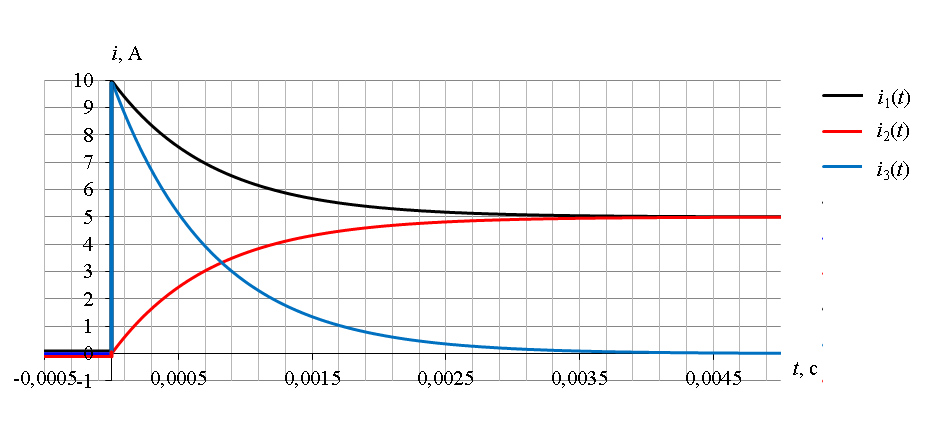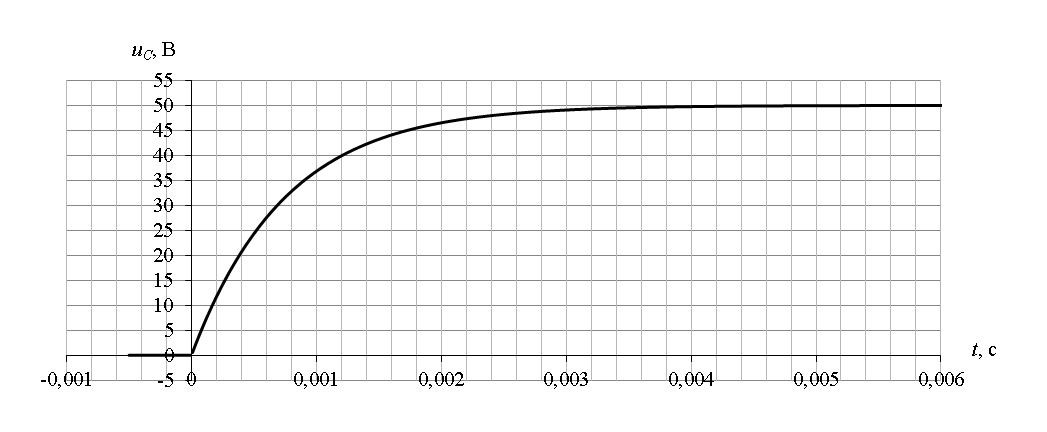

Задача 2

Для магнитной цепи, изображенной на рис. 8, выполнить следующее:

1. Начертить эквивалентную схему, указав на ней направления магнитных потоков и магнитодвижущих сил (МДС).

2. Составить для магнитной цепи систему уравнений по законам Кирхгофа.

3. Определить магнитные потоки в стержнях и значение магнитной индукции в воздушном зазоре. Размеры магнитопровода на рис. 8 даны в мм. Магнитопровод выполнен из электротехнической стали, кривая намагничивания которой представлена в табл.2. Величины токов и число витков обмоток для каждого варианта даны в табл. 3. При расчете цепи магнитными потоками рассеяния пренебречь

Дано: I₁ = 15 А; w₁ = 200; I₂ = 45 А; w₂ = 100.

B, Тл	0	0,4	0,8	1,2	1,6	2
H, А/м	0	200	400	950	3900	15000

Решение

Э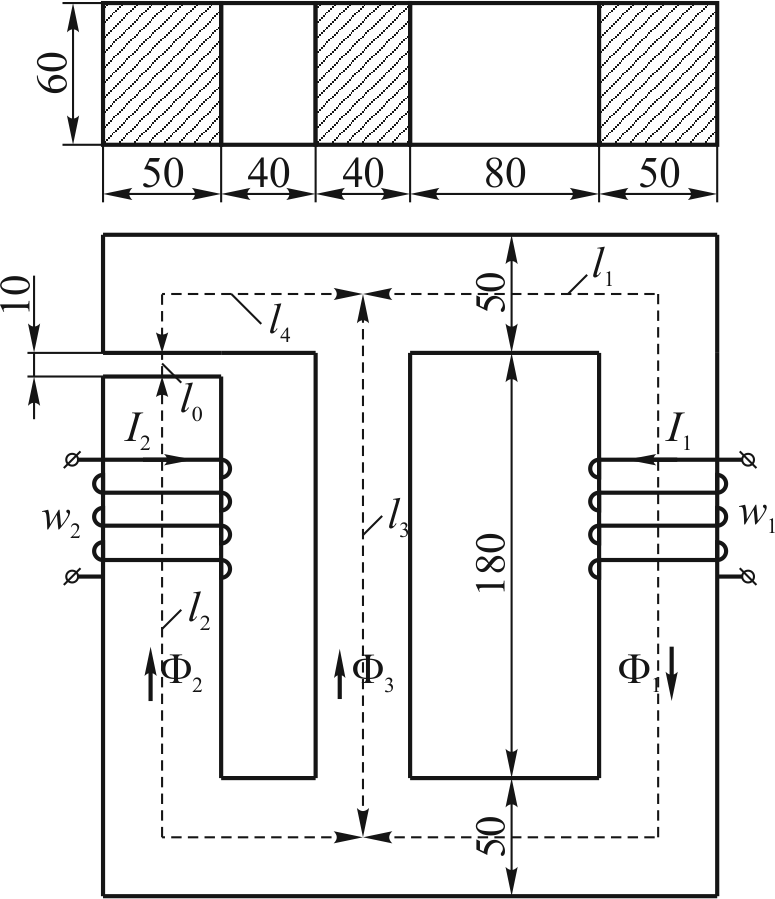

квивалентная схема

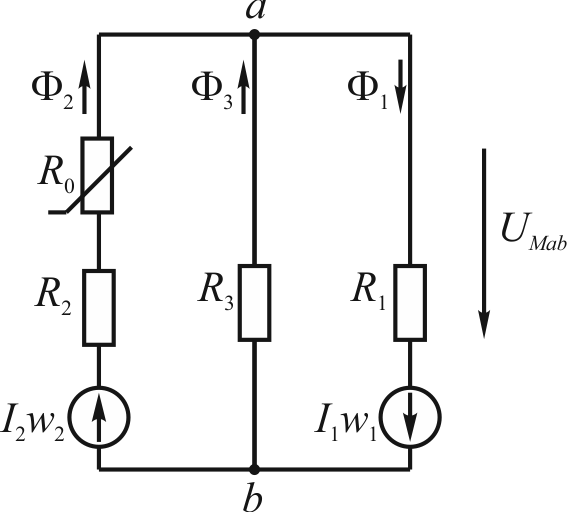Длины участков сердечника

l₁ = 2∙(40/2 + 80 + 50) + 180 = 480 мм;

l₂ = 40/2 + 40 + 50 + 180 – 10 = 320 мм;

l₃ = 180 + 50 = 230 мм;

l₄ = 40/2 + 40 + 50 = 150 мм;

l₀ = 10 мм.

Площади сечений участков сердечника

S₁ = S₂ = 50∙60 = 3000 мм²;

S₃ = 40∙60 = 2400 мм².

Система уравнений по законам Кирхгофа

– ₁ + ₂ + ₃ = 0;

I₂w₂ = H₂(l₂ + l₄) – H₃l₃ + H₀l₀;

I₁w₁ = H₁l₁ + H₃l₃.

Магнитодвижущие силы I₁w₁ = 15∙200 = 3000 А; I₂w₂ = 45∙100 = 4500 А.

Построение зависимости магнитодвижущей силы от магнитного потока в среднем стержне.

Принимается магнитная индукция в стержне с зазором B₀ = B₂.

Напряженность магнитного поля в воздушном зазоре H₀ = 0,8B₀∙10⁶.

Напряженность магнитного поля

в левом стержне H₂ определяется по кривой намагничивания;

в среднем стержне H₃ = (– I₂w₂ + H₂(l₂ + l₄) + H₀l₀)/l₃;

в правом стержне H₁ = (I₁w₁ – H₃l₃)/l₁.

Магнитные индукции в среднем и правом стержнях B₃ и B₁ определяются по кривой намагничивания.

Магнитные потоки в каждом стержне и воздушном зазоре ₁ = B₁S₁; ₂ = B₂S₂; ₃ = B₃S₃.

Межузловое магнитное напряжение для каждой ветви

U_м₁ = H₁l₁ – I₁w₁; U_м₂ = H₂(l₂ + l₄) + H₀l₀ – I₂w₂; U_м₃ = H₃l₃.

B₀, B₂, Тл	H₀, ∙10⁶ А/м	H₂, А/м	H₁, А/м	H₃, А/м	B₁, Тл	B₃, Тл	₁, мВб	₂, мВб	₃, мВб	U_м1, А	U_м₂, А	U_м₃, А	, мВб
0,567	0,4536	283,5	5897	736	1,67	1,04	5,02	1,70	3,13	169	169	169,2	0,18
0,568	0,4544	284,0	5880	772	1,67	1,07	5,01	1,70	3,21	177	177	177,5	0,10
0,569	0,4552	284,5	5863	807	1,67	1,10	5,01	1,71	3,29	186	186	185,7	0,02
0,570	0,456	285,0	5846	843	1,67	1,12	5,01	1,71	3,37	194	194	193,9	-0,07
0,571	0,4568	285,5	5829	879	1,67	1,15	5,01	1,71	3,45	202	202	202,2	-0,15
0,572	0,4576	286,0	5812	915	1,67	1,17	5,01	1,72	3,52	210	210	210,4	-0,23
0,573	0,4584	286,5	5794	951	1,67	1,20	5,00	1,72	3,60	219	219	218,7	-0,32

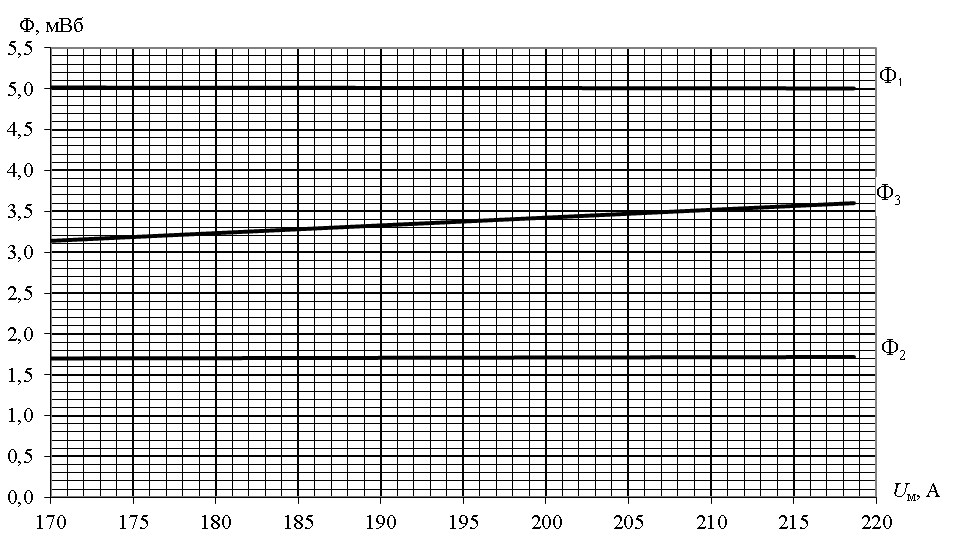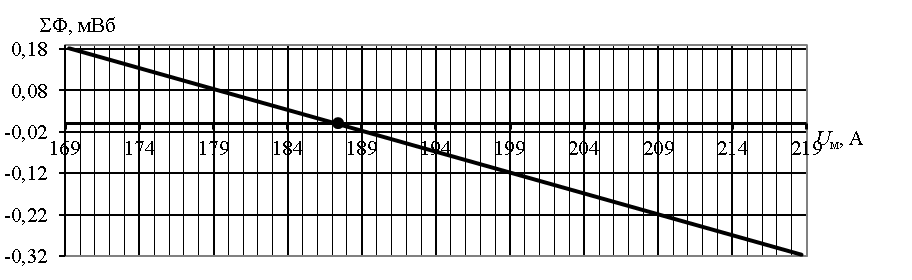Магнитное напряжение при  = 0: U_м = 17 А.

Магнитные потоки по графику ₁ = 35,2 мВб; ₂ = 1,71 мВб; ₃ = 3,3 мВб.

Магнитная индукция в воздушном зазоре B₀ = ₂/S₂ = 1,71∙10³/3000 = 0,569 Тл.
Задача 3

В табл. 2 заданы основные парамегры выпрямителя:

U_н_.ср – среднее значение выпрямленного напряжения на нагрузке:

I_н_.ср – среднее значение выпрямленного тока;

Напряжение питающей сети U₁ = 220 В.

Требуется:

Начертить принципиальную электрическую схему однофазного мостового выпрямителя и описать его работу.

Выбрать тип диодов выпрямителя.

Рассчитать действующие значения напряжения вторичной обмотки трансформатора U₂, токов обмоток трансформатора I₁ и I₂.

Определить габаритную мощность трансформатора.

Построить временные диаграммы

а) напряжения и тока во вторичной обмотке трансформатора

б) напряжения и тока в активной нагрузке.

Дано: U_н.ср = 5 В; I_н.ср = 1 В.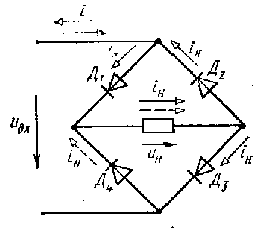

Ток нагрузки мостового выпрямителя I_н направлен в одну и ту же сторону и обеспечивается диодами
Д1 и Д3 в положительный полупериод входного напряжения u_вх и диодами Д2 и Д4 в отрицательный полупериод.

Максимальное обратное напряжение на диодах

U_{обр.макс} = 1,57U_н.ср = 1,57∙5 = 7,85 В.

Средний прямой ток каждого диода

I_пр.ср = 0,5I_н.ср = 0,5∙1 = 0,5 В.

Необходимые параметры диода

I_пр.д = 1,3I_пр.ср = 1,3∙0,5 = 0,650 В.

U_{обр.макс.д} = 1,3U_{обр.макс} = 1,3∙7,85 = 10,21 В.

Выбирается диод типа КД221А с характеристиками:

допустимое обратное напряжение U_обр._max = 100 В;

выпрямленный ток I_пр.ср = 0,7 А;

падение напряжения в прямом направлении U_пр = 1,4 В;

постоянный обратный ток I_обр = 50 мкА.

Действующее значение напряжения вторичной обмотки трансформатора

U₂ = 1,11U_н.ср = 1,11∙5 = 5,55 В.

Коэффициент трансформации

n = U₁/U₂ = 220/5,55 = 39,64.

Сопротивление нагрузки

R_н = U_н.ср/I_н.ср = 5/1 = 5 Ом.

Действующее значение тока вторичной обмотки трансформатора

I₂ = U₂/R_н = 5,55/5 = 1,11 А.

Действующее значение тока первичной обмотки трансформатора

I₁ = I₂/n = 1,11/39,64 = 0,028 А.

Габаритная мощность трансформатора для однофазной мостовой схемы выпрямления

S_г = 1,23U₂I₂ = 1,23∙5,55∙1,11 = 7,58 В∙А.

Частота питающего напряжения

f = 50 Гц.

Угловая частота питающего напряжения

 = 2f = 2∙3,14∙50 = 314 рад/с.
Амплитуда напряжения во вторичной обмотке трансформатора

U₂_m = U₂ sin(t) = 5,55∙1,414 = 7,85 В;

I₂_m = I₂ sin(t) = 1,11∙1,414 = 1,57 В.

Временная диаграмма напряжения и тока во вторичной обмотке трансформатора

u₂(t) = U₂_m sin(t) = 7,85 sin(314t);

i₂(t) = I₂_m sin(t) = 1,57 sin(314t).

Временная диаграмма напряжения и тока в активной нагрузке

u₂(t) = U₂_m sin(t) = 7,85 |sin(314t)|;

i₂(t) = I₂_m sin(t) = 1,57 |sin(314t)|.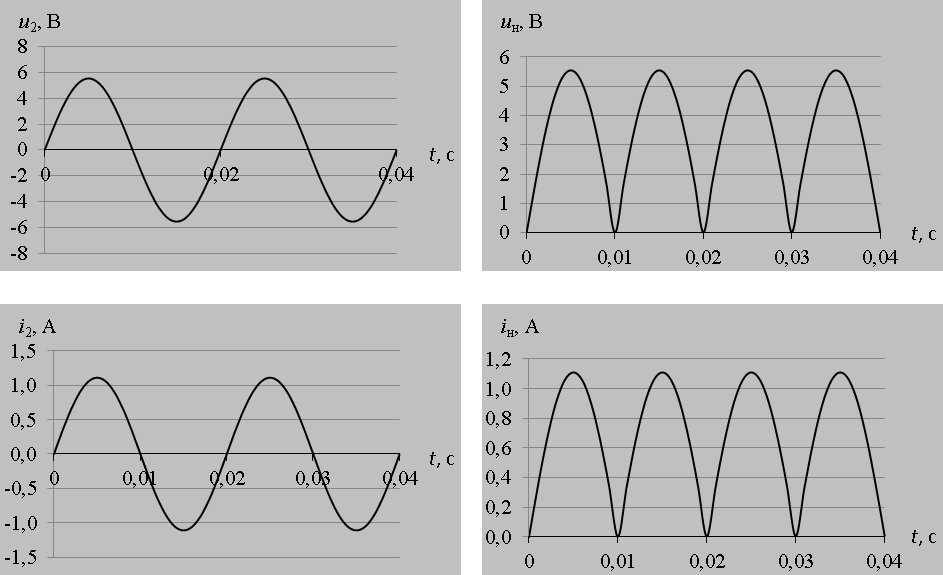

Основная литература
1. Теоретические основы электротехники: В 3-х т. Учебник для вузов. Том 2/ К. С. Демирчян,
Л. Р. Нейман, Н. В. Коровкин – СПб.: Питер, 2009 (в ЭБС «Айбукс»).

2. Чижма С.Н. Электроника и микросхемотехника. М.: УМЦ ЖДТ, 2012 (в ЭБС «Айбукс»).
Дополнительная литература
3. Серебряков А.С. Электротехника. Магнитные цепи: учебное пособие. – 3-е изд. перераб. и доп. –
М.: РГОТУПС, 2007. - Утверждено редакционно-методическим. советом РГОТУПСа (в библ. РОАТ).

4. Климентов Н.И. Теоретические основы электротехники. Нелинейные электрические и магнитные цепи постоянного тока. Учебное пособие. – М.: РГОТУПС, 2010 (в библ. РОАТ).

5 Серебряков А.С. Нелинейные электрические и магнитные цепи переменного тока. Конспект лекций. –
М.: РГОТУПС, 2009 (в библ. РОАТ).

6 Серебряков. А.С. Mathcad и решение задач электротехники: учеб. пособ. / А.С. Серебряков, В.В. Шумейко. - М.: Маршрут, 2005 (в библ. РОАТ).

7. Частоедов Л.А., Ручкина Л.Г., Гирина Е.С. Теоретические основы электротехники. Электротехника и электроника. Ч.2., Методические указания по решению задач для студентов II курса. – М.: РГОТУПС, 2008 (в СДО КОСМОС).

8. Электротехника и электроника. Учебник для вузов. – В 3-х кн. Кн. 3. Электрические измерения и основы электроники/ Г.П. Гаев, В.Г. Герасимов, О.М. Князьков и др.; Под ред. проф. В.Г. Герасимова. – Энергоатомиздат, 1998 (в библ. РОАТ).