КР (1). Решение 5 Построение спецификации эконометрической модели 5 Оценка параметров модели парной регрессии 5
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
СодержаниеЗадание 2 Условие вариант 18. 3 Решение 5 1. Построение спецификации эконометрической модели 5 2. Оценка параметров модели парной регрессии 5 3. Оценивание качества спецификации модели 7 4. Проверка предпосылки теоремы Гаусса-Маркова об отсутствии автокорреляции случайных возмущений 9 12 5. Множественная регрессия 12 6. Прогнозирование экзогенной переменной 15 7. Прогнозирование эндогенной переменной 17 8. Представить результаты моделирования и прогнозирования в графическом формате 19 ЗаданиеПостроение спецификации эконометрической модели Привести постановку задачи построения модели парной линейной регрессии. Выбрать эндогенную переменную. Сделать предположения относительно знаков (положительный или отрицательный) параметров модели. Оценка параметров модели парной регрессии Оцените параметры модели. Выпишите полученное уравнение регрессии. Дайте экономическую интерпретацию параметрам модели. Оценивание качества спецификации модели Проверить статистическую значимость регрессии в целом. Проверить статистическую значимость оценок параметров. Оценить точность модели с помощью средней относительной ошибки аппроксимации. Сделайте выводы качестве уравнения регрессии. Проверка предпосылки теоремы Гаусса-Маркова об отсутствии автокорреляции случайных возмущений Выполнить визуальный анализ автокорреляции остатков с помощью графика. Привести результаты тестирования на отсутствие автокорреляции случайных возмущений с помощью теста Дарбина -Уотсона. Сделать выводы. При необходимости предложить вариант корректировки автокорреляции. Множественная регрессия В связи с тем, что объясняющая переменная представляет собой временной ряд, одной из составляющих компонент которого может быть сезонная волна, необходимо учесть эту структуру для дальнейшего прогноза, введя фиктивные переменные для соответствующих кварталов. Постройте график изменения объясняющей переменной - индекс реальных инвестиций в основной капитал во времени с целью визуального выявления сезонной волны. Постройте многофакторную модель динамики объясняющей переменной. Оцените качество и значимость модели и отдельных ее параметров. Поясните экономический смысл параметров при фиктивных переменных сдвига при исследовании сезонных колебаний. Прогнозирование экзогенной переменной Использовать построенную многофакторную модель с фиктивными переменными для прогнозирования экзогенной переменной на ближайшие четыре квартала. Привести график. Прогнозирование эндогенной переменной Используя прогнозную оценку потребности в работниках, построить точечный и интервальный прогноз с вероятностью 0,9 (α=0,1) исследуемой нормы безработицына ближайшие четыре квартала. Представить результаты моделирования и прогнозирования в графическом формате Условие вариант 18.Ставится задача исследовать, как влияет заявленная потребность в работниках (в тыс.чел.) (EMPLDEC_Q) на норму безработицы в среднем за период в млн. чел. (UNEMPL_Q_SH) в России.
Решение1. Построение спецификации эконометрической моделиТребуется исследовать, как влияет размер заявленная потребность в работниках (в тыс.чел.) (EMPLDEC_Q) на норму безработицы в среднем за период в млн. чел. (UNEMPL_Q_SH) в России. Экзогенная, независимая переменная – размер заявленной потребности в работниках. А эндогенная, зависимая переменная – норма безработицы в среднем за период. Парная линейная регрессия определяется моделью вида: 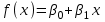 , ,в обозначениях задачи: 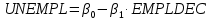 . .Предполагаем, что рост потребности в работниках ведет к снижению нормы безработицы, поэтому ожидаем, что коэффициент регрессии 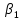 модели будет отрицательным. модели будет отрицательным.2. Оценка параметров модели парной регрессии1) Исходные данные импортируем в Gretl как временные ряды (квартальные данные): 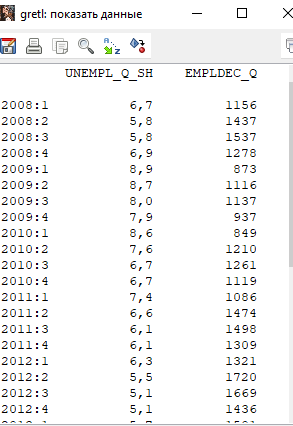 2) Оценим параметры модели в Gretl (Модель / Метод наименьших квадратов). Окно с результатами: 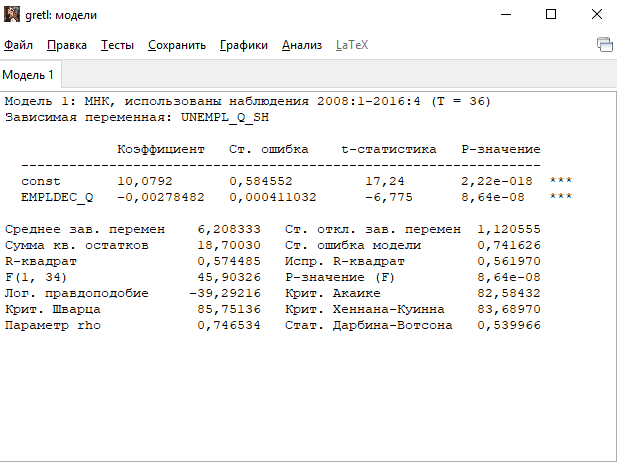 Рис. 1 Результат оценки параметров модели МНК. Уравнение линейной регрессии: 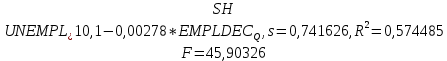 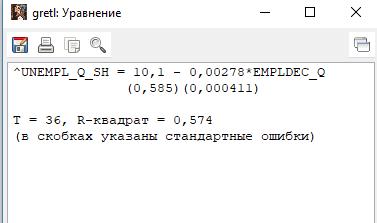 Рис.2 Уравнение линейной регрессии в Gretl Интерпретация параметров модели: при увеличении заявленной единицы работников на 1 ед. норма безработицы в среднем уменьшается на 0,00278%. 3. Оценивание качества спецификации моделиКоэффициент детерминации R2=0,574. Он показывает долю вариации (дисперсии) результативного признака под воздействием изучаемых факторов. Следовательно, около 57,4% вариации зависимой переменной учтено в модели и обусловлено влиянием включенного фактора, а 42,6% приходится на прочие не учтенные в модели факторы. Используя информацию, приведенную на рис.1, можно проверить значимость всего уравнения регрессии в целом по критерию Фишера и значимость отдельных коэффициентов. Согласно рис.1 𝐹выч = 𝐹(1, 34)= 45,90326. 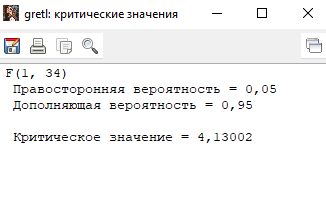 Рис.3. Получение критического значения критерия Фишера Так как 𝐹выч = 45,9 > 𝐹крит = 4,13002 (рис.3), то модель значима. Нулевая гипотеза H0: R2=0, отвергается и, коэффициент детерминации признается статистически значимым (регрессия в целом статистически значима). для проверки значимости модели регрессии можно воспользоваться Р-значением (F). В Р-значении содержится вероятность ошибки первого рода при тестировании гипотезы, Р-значение показывает вероятность ошибиться, отвергнув гипотезу H0, при том, что она верна. Значение критерия Фишера равно 45,9. Р-значение (F) равно 8,63722042575011E-08 (рис. 1). Это говорит о том, что можно отвергнуть гипотезу H0 (вероятность ошибки близка к нулю). Критерий Стьюдента. При проверке гипотезы 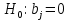 против альтернативной гипотезы против альтернативной гипотезы 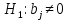 , для коэффициентов , для коэффициентов 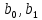 рассчитывается абсолютная величина t -статистики: рассчитывается абсолютная величина t -статистики: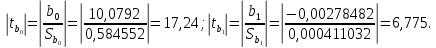 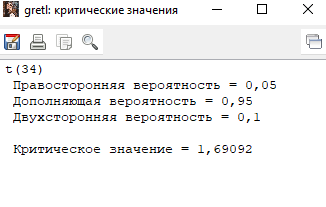 Рис.4. Получение критического значения критерия Стьюдента Критическое значение 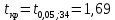 (рис.4). Так как (рис.4). Так как 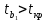 , то b1 значимый на 5% уровне и заявленная потребность в работниках оказывает значимое влияние на норму безработицы. Для свободного члена , то b1 значимый на 5% уровне и заявленная потребность в работниках оказывает значимое влияние на норму безработицы. Для свободного члена 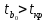 , он значим на 5% уровне. , он значим на 5% уровне.На следующем этапе найдем значение средней относительной ошибки аппроксимации. Для этого в модели нужно выбрать Анализ / Наблюдаемые и расчетные значения.  Рис.5. Средняя относительная ошибка аппроксимации Значение MAPE – это средней относительной ошибкой аппроксимации: 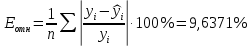 фактические уровни доходов населения отличаются от расчетных в среднем на 9,6371%. Значение превысило 7%, что говорит о невысокой точности модели. 4. Проверка предпосылки теоремы Гаусса-Маркова об отсутствии автокорреляции случайных возмущенийПостроим график остатков с помощью Gretl (Модель/График/График остатков): 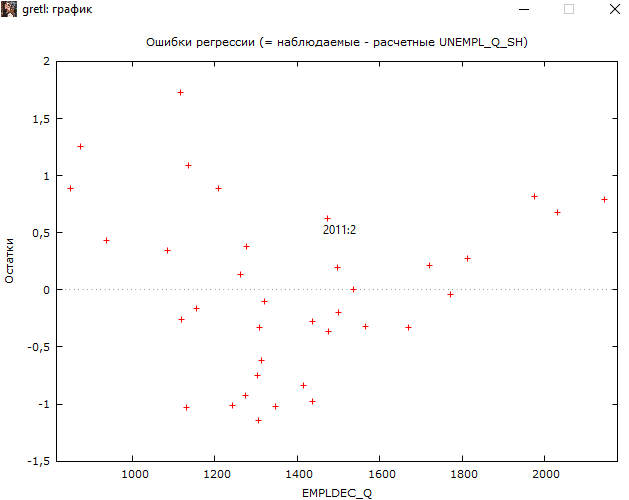 Рис.6. График остатков Визуальное распределение (рис.6) остатков свидетельствует о случайном характере связей между отклонениями, поэтому предполагаем отсутствие автокорреляции остатков. В соответствии с алгоритмом теста Дарбина-Уотсона по формуле: 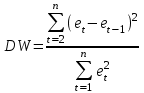 вычислим значение статистики теста. вычислим значение статистики теста. Выполним тест Дарбина-Уотсона в программе GRETL: Тесты / p - значение статистики Дарбина–Уотсона. 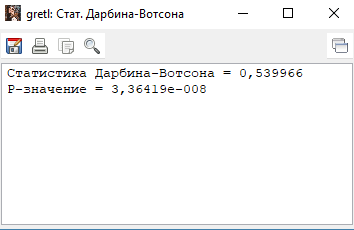 Рис.7. Тест Дарбина – Уотсона. 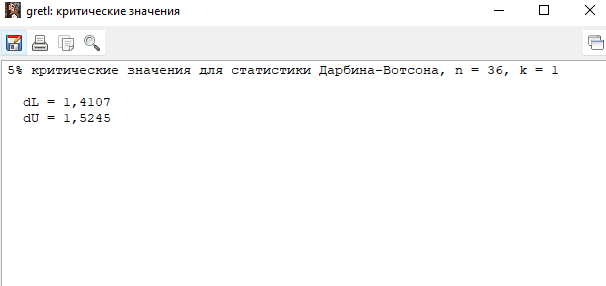 Рис.8. Критическое значение Дарбина – Уотсона. Расположим на графике: 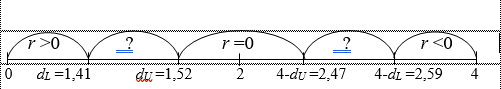 Рис.9. Анализ значений Дарбина – Уотсона Вычисленное значение статистики dU =1,52> DW=0,54 попадает в первый интервал, свойство независимости не выполняется, поэтому модель нужно корректировать. Гипотеза об отсутствии автокорреляции отвергается.  Для корректировки модели используем процедуру Хильдрата-Лу: Для корректировки модели используем процедуру Хильдрата-Лу:Рис. 10. Результаты процедуры Хильдрата-Лу Значение Дарбина – Уотсона = 1,43, находится в промежутке между критическими значениями модели. Отсюда следует, что автокорреляция отсутствует. Ниже представлено уравнение по скорректированной модели: 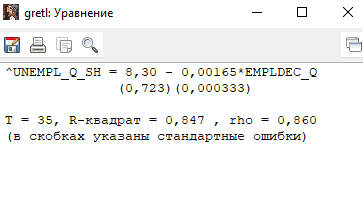 5. Множественная регрессияПостроим график изменения потребности в работниках во времени. 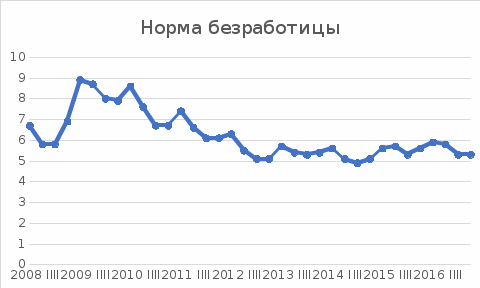 Рис.11. Изменение во времени По графику прослеживается сезонность, поэтому необходимо ввести эту структуру в модель для дальнейшего прогноза. Запишем спецификацию регрессионной модели с фиктивными переменными сдвига, учитывающими сезонные колебания 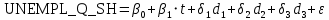 , , 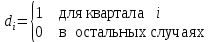 , , 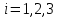 . .Построим МНК в Gretl: 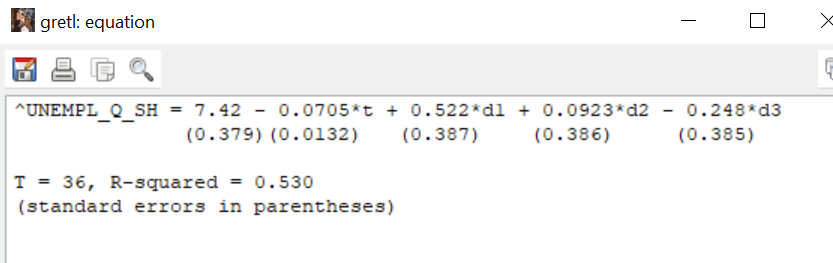 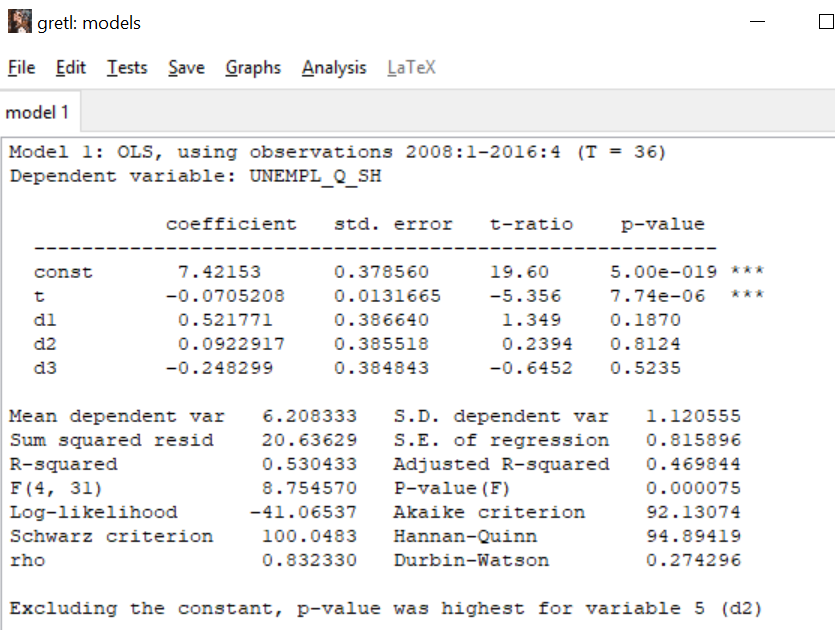 Рис.12. Полученные результаты Интерпретация параметров модели: -0,071 показывает, что с каждым кварталом норма безработицы в среднем снижается на 0,071%. Остальные коэффициенты показывают, как изменяется показатель в зависимости от сезона. В данной модели 4 квартал базовый, значит, в начальный момент времени (при t=0) норма безработицы в 4 квартале составляет 7,42%. Коэффициенты сдвига di показывают следующее: в 1 квартале года норма увеличивается на 0,52% по сравнению с 4 кварталом (при неизменных значениях остальных параметров), во 2 квартале года увеличивается на 0,09% по сравнению с 4 кварталом (при неизменных значениях остальных параметров), в 3 квартале года снижается на 0,25% по сравнению с 4 кварталом (при неизменных значениях остальных параметров). Критерий Фишера: Fнабл = 8,75 > Fтаб = 2,67, т.е. полученная модель статистически значима в целом на 5% уровне. 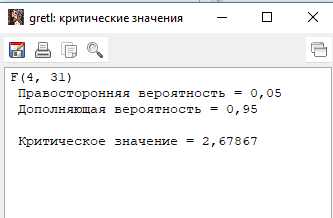 Значения t-статистик в результатах моделирования по модулю больше критического (1,7), значит, параметры значимы на 5% уровне. Незначимы параметр 1 квартала. 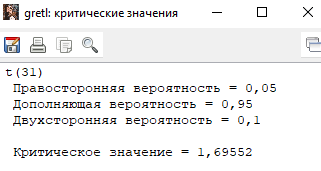 Оценим точность модели с помощью средней относительной ошибки аппроксимации: 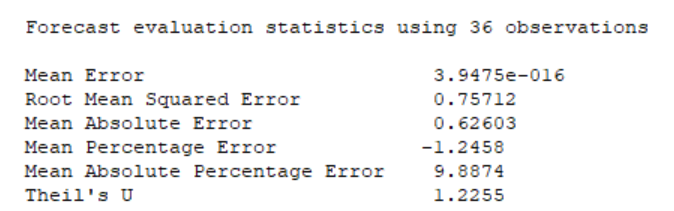 Фактические уровни нормы безработицы отличаются от расчетных в среднем на 9,89%. Значение превышает 7%, что говорит о низкой точности модели. 6. Прогнозирование экзогенной переменнойИспользовать построенную многофакторную модель с фиктивными переменными для прогнозирования размера заявленной потребности в работниках на ближайшие четыре квартала. Для этого предварительно добавим 4 наблюдения:  Прогноз: 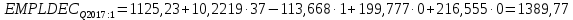 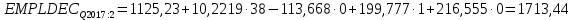 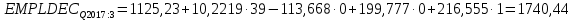 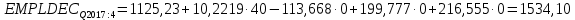 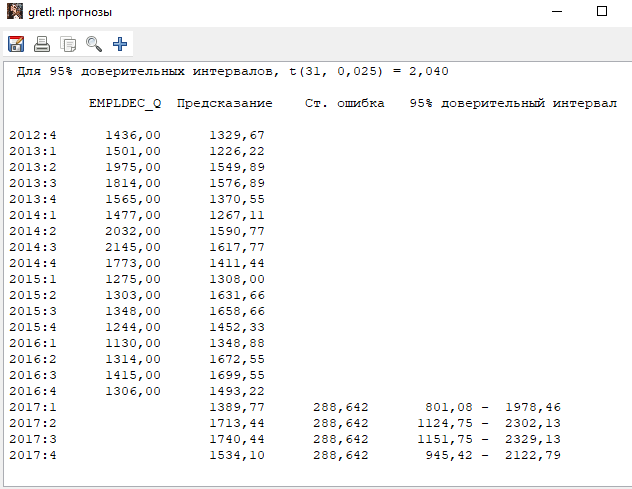 График: 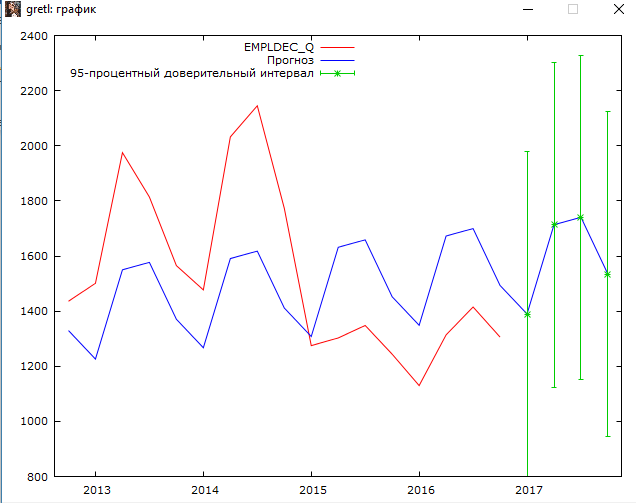 7. Прогнозирование эндогенной переменнойМодель с учетом добавленных параметров и прогнозных значений экзогенной переменной. 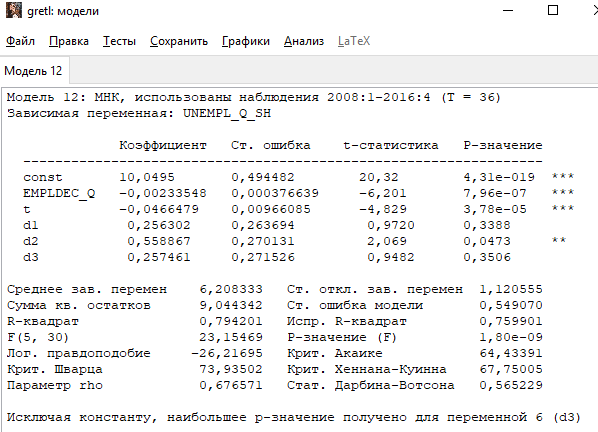 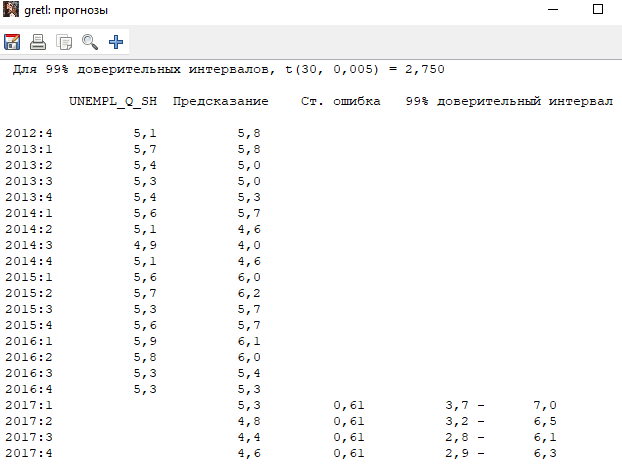 Точечный и интервальный прогноз нормы безработицы на 4 квартала 2017 года: Точечный и интервальный прогноз нормы безработицы на 4 квартала 2017 года: Таким образом, в 1 квартале 2017 г. при прогнозируемой потребности в работниках 1389,77 норма безработицы с вероятностью 0,9 будет находиться в пределах от 3,7 до 7%, во 2 квартале при потребности 1713,44 интервал 3,2-6,5%; 3 квартал при 1740,44 – 2,8-6,1; в 4 – при 1534,10 – 2,9-6,3. График: 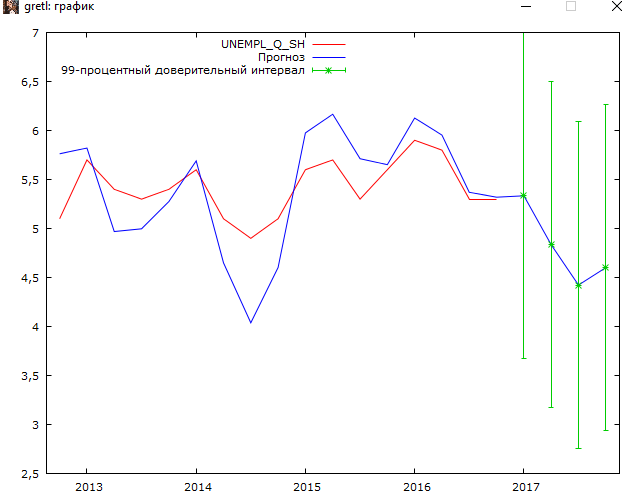 8. Представить результаты моделирования и прогнозирования в графическом формате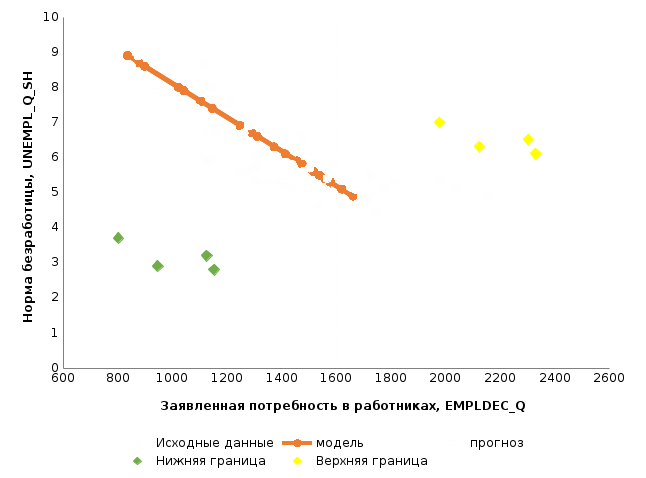 Фактические значения располагаются близко от оцененной прямой, что говорит о хорошем качестве построенной модели. Делаем выводы о достоверности прогнозов. |
