высшая математика. Математика (4,16,26,35). Решение а Представим данный ряд как геометрическую прогрессию

• Название: Решение а Представим данный ряд как геометрическую прогрессию
• Анкор: высшая математика
• Дата: 11.01.2023
• Размер: 159.5 Kb.
• Имя файла: Математика (4,16,26,35).doc
• Тип: Решение; #881727

Математика 5

№: 4, 16, 26, 35

№ 4
Найти сумму ряда:

а) ; б)
Решение:
а) :

Представим данный ряд как геометрическую прогрессию:



Получили бесконечно убывающую геометрическую прогрессию со знаменателем q = 1/14 и q = 1/6, ее сумму определим по формуле:



Ответ:
б)

Для начала разложим выражение в знаменателе на скобки:



Тогда получим:



Так как нижний предел суммирования не равен 1 (в нашем случае он равен 9), то выражение

 не является общим членом ряда.

Изменим нижний предел суммирования на 1:

Введём новый индекс таким образом, чтобы его начальное значение равнялось 1. Этот новый индекс суммирования обозначим буквой k.

Итак, если n = 9, то k = 1 = n – 8, т.е. n = k + 8. Подставляем в знаменатель  вместо n выражение (k + 8). При этом не забываем, что новый индекс изменяется с 1, тогда получаем:



Так как нижний предел суммирования равен 1, то общий член ряда:



Разложим дробь на элементарные дроби:



Приравниваем числители дробей в левой и правой частях полученного равенства:



Приравнивая коэффициенты, имеем:



Тогда, получаем:



Т.е.

Составим частичные суммы для этого ряда:











В сумме S₄ уничтожаются слагаемые с 6/4 , в сумме S₅ уничтожаются слагаемые с 6/5 и т. д. Все частичные суммы будут состоять из 6 слагаемых. Запишем S_k, учитывая, что шестое слагаемое получается из последнего слагаемого k a при подстановке k = k, пятое слагаемое получается из того же самого слагаемого при k  k – 1 и четвертое при k  k – 2. Таким образом:

Находим -ю частичную сумму:


Тогда сумма ряда будет равна:


Ответ:

№ 16

Проверить необходимое условие сходимости числового ряда:

а) ; б)
Решение:
а) ;

Выпишем общий член ряда:

Найдем предел:



Так как предел общего члена ряда равен нулю, то необходимый признак сходимости выполнен. Следовательно, ряд сходится.
б)

Выпишем общий член ряда:

Найдем предел: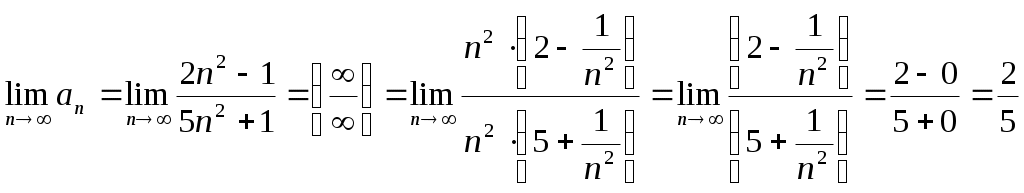



Так как предел общего члена ряда не равен нулю, то необходимый признак сходимости не выполнен. Следовательно, ряд расходится.

№ 26

Исследовать на сходимость ряды с положительными членами:

а) ; б)
Решение:
а) :

Воспользуемся признаком Даламбера:

Выпишем общий член ряда:

Далее запишем:

Найдем предел отношения:



Так как q > 1, то по признаку Даламбера делаем вывод, что ряд расходится.

б)
В данном случае воспользуемся признаком Коши:

Выпишем общий член ряда:

Найдем предел:



Так как q > 1, то по признаку Коши делаем вывод, что ряд расходится.

№ 35

Разложить функцию в ряд Маклорена с указанной точностью:


Решение:
Поскольку требуется получить разложение с точностью o(х⁶), то искомая формула должна иметь вид:



Воспользуемся известным разложением элементарной функции в ряд Маклорена:



Тогда, с учетом того, что получим:







Список литературы:
1. Бугров, Я.С. Высшая математика в 3 т. Т.3 в 2 книгах. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного: Учебник / Я.С. Бугров, С.М. Никольский. – Люберцы: Юрайт, 2016. – 507 c.

2. Клюшин, В.Л. Высшая математика для экономистов.: Учебное пособие для бакалавров / В.Л. Клюшин. – Люберцы: Юрайт, 2016. – 447 c.

3. Лурье, И.Г. Высшая математика. Практикум: Учебное пособие / И.Г. Лурье, Т.П. Фунтикова. – М.: Вузовский учебник, 2018. – 256 c.

4. Шипачев, В.С. Высшая математика. полный курс в 2 т. том 2: Учебник для академического бакалавриата / В.С. Шипачев. – Люберцы: Юрайт, 2016. – 341 c.