Линейная алгебра и аналитическая геометрия. Контрольная работа. конт.алгебра№1. Решение а диагоналями параллелограмма являются векторы и найдем их Тогда
 Скачать 118.13 Kb. Скачать 118.13 Kb.
|
|
К/р №1 Линейная алгебра и аналитическая геометрия. 1. На векторах 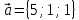 и и 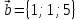 построен параллелограмм. Найти: построен параллелограмм. Найти:а) угол между диагоналями параллелограмма б) площадь параллелограмма, в) высоту параллелограмма, опущенную на вектор 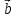 . .Решение: а) диагоналями параллелограмма являются векторы 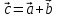 и и 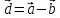 найдем их: 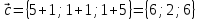 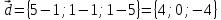 Тогда  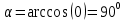 б) Площадь паралелограмма, построенного на векторах равна модулю их векторного произведения: 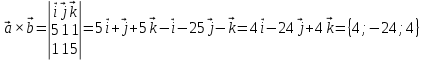  Следовательно, площадь параллелограмма равна  в) Площадь параллелограмма можно найти и другим способом: 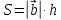 Следовательно, зная площадь параллелограмма и длину вектора на которую опущена высота, можно найти высоту. Площадь параллелограмма мы уже знаем 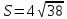 , найдем длину вектора , найдем длину вектора 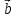 : :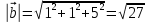 тогда 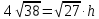 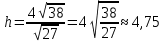 2. Даны координаты вершин пирамиды ABCD: A(6,1,1), B(1,6,1), C(1,1,6), D(0,0,0). Найдите: а) модуль вектор 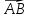 ; ;б) объем пирамиды; в) длину высоты опущенной из вершины D. Решение: а) найдем вектор 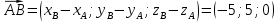 Длина вектора (модуль вектора): 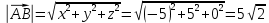 б) Объем пирамиды АВСD найдем используя смешанное произведение векторов 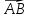 , , 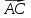 и и  . . Найдем вектора: 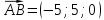 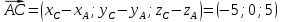  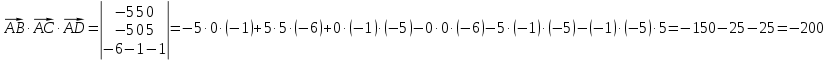 Как считаем, рисую схему: 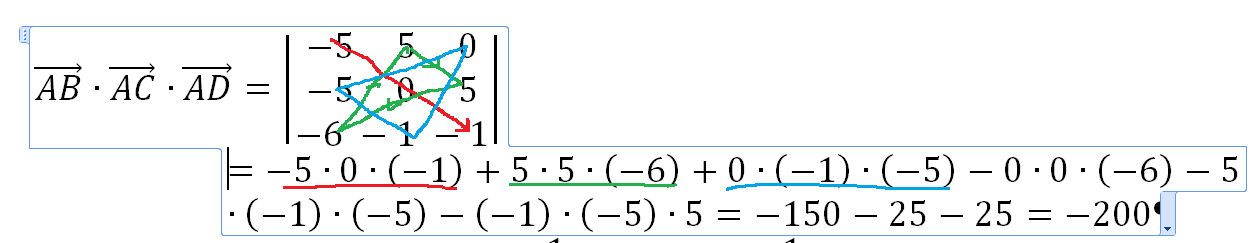 дальше с минусом часть в формуле  Дальше везде, где ищем определить матрицы, пользуемся этим методом. 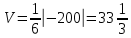 в) Длину высоты, опущенной из вершины D на грань АВС найдем, как расстояние точки D(0;0;0) до плоскости АВС:  Найдем вектор нормали через векторное произведение векторов  : :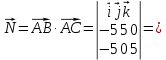 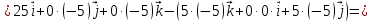 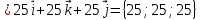 Сократим на 25 и получим вектор нормали: 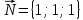 Уравнение грани АВС запишем используя ее вектор нормали N и координаты точки А:  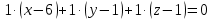 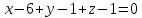 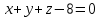 Длина высоты:  3. В условиях предыдущей задачи найдите: а) уравнение плоскости АВС б) уравнение высоты опущенной из вершины D; в) точку пересечения этой высоты с основанием. Решение: а) уравнение плоскости АВС мы уже нашли: 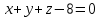 б) Прямая, проходящая через точку M0(x0;y0;z0) и перпендикулярная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется симметричными уравнениями: 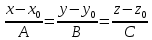 Уравнение плоскости АВС: 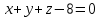 и точка D(0,0,0): и точка D(0,0,0):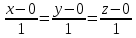 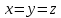 в) переведем найденное уравнение к параметрическому виду: 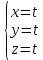 Подставим в уравнение плоскости: 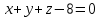   Находим координаты точки пересечения прямой и плоскости по параметрическим уравнениям при 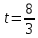  Следовательно, точка пересечения высоты с основанием: 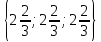 4. Даны матрицы Q, S, D. Найдите: а) S + DT б) Q-1 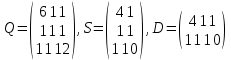 Решение: а) Найдём транспонированную матрицу DT: DT=  Тогда S + DT= 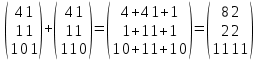 б) Найдем определитель матрицы   Вычислим алгебраические дополнения Аij к соответствующим элементам матрицы А: 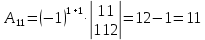 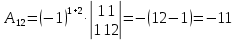  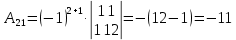 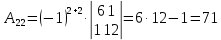 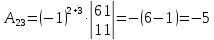  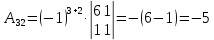 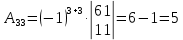 Запишем из полученных дополнений Q* - союзная матрица 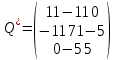 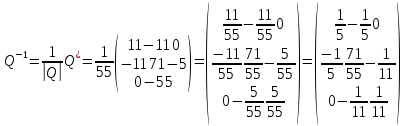 Получили 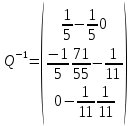 5. Решить систему уравнений: а) с помощью обратной матрицы 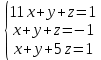 Решение: Метод обратной матрицы используется при решении систем линейных алгебраических уравнений, если число неизвестных равно числу уравнений, проверим число уравнений 3, число неизвестных 3. Эту систему можно записать в виде матричного уравнения  , где , где 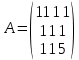 - матрица система, - матрица система, 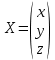 - столбец неизвестных, - столбец неизвестных, - столбец свободных коэффициентов. - столбец свободных коэффициентов.Из полученного матричного уравнения необходимо выразить Х. Для этого умножим обе части матричного уравнения слева на  , получим: , получим: Найдем определитель матрицы:     значит система имеет единственное решение, которое можно найти методом обратной матрицы. значит система имеет единственное решение, которое можно найти методом обратной матрицы.Найдем обратную матрицу А-1 с помощью союзной матрицы. Вычислим алгебраические дополнения Аij к соответствующим элементам матрицы А:  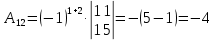  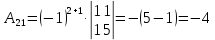 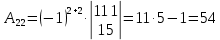 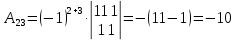    Запишем из полученных дополнений А* - союзная матрица   Умножая обратную матрицу 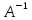 на столбец свободных членов В, получим искомое решение исходной системы: на столбец свободных членов В, получим искомое решение исходной системы: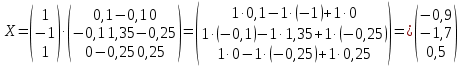 Следовательно, решением системы является:x = - 0,9; y = -1,7; z = 0,5 б) методом Гаусса, указать фундаментальную систему решений соответствующей однородной системы и записать общее решение в векторной форме: 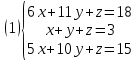 Решение: Убедимся в том, что система совместна: Составляем матрицу А: 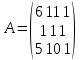 Составим расширенную матрицу 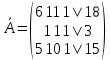 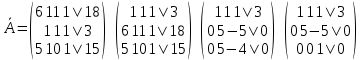 показываю что делаем:  Итак, R(A) = R( 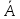 ) = 3 – система совместна. ) = 3 – система совместна. Так как ранг матрицы А равен 3 и равен числу неизвестных - три. Значит, однородная система не имеет свободных неизвестных, а поэтому имеет единственное решение – тривиальное. Составим приведенную однородную систему (2) для системы (1), заменив в (1) все свободные члены нулями. Затем найдем единственное решение системы (2) методом Гаусса: 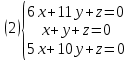  Решением однородной системы является:  Решим систему линейных уравнений методом Гаусса  Решением неоднородной системы:  Общее решение неоднородной системы линейных уравнений является суммой общего решения соответствующей однородной системы и частного решения неоднородной системы, т.е.  Ответ: Общее решение системы:  6. Докажите, что векторы  , ,  , ,  образуют базис и найдите координаты вектора образуют базис и найдите координаты вектора  в этом базисе: в этом базисе: Решение: Векторы образуют базис, если определитель, составленный из координат этих векторов, отличен от нуля, в противном случае вектора не являются базисными и вектор X нельзя разложить по данному базису. Составим матрицу и вычислим определитель этой матрицы:     Так как определитель отличен от нуля, то векторы образуют базис, следовательно, вектор  можно разложить по данному базису. Т.е. существуют такие числа α1, α2, α3, что имеет место равенство можно разложить по данному базису. Т.е. существуют такие числа α1, α2, α3, что имеет место равенство Запишем данное равенство в координатной форме:  Используя свойства векторов, получим следующее равенство:   По свойству равенства векторов имеем:  Решим данную систему методом Гаусса:  Значит, найдите координаты вектора  в этом базисе в этом базисе  . . |
