Теория вероятностей. МУБиНТ. Вариант №34.. Решение а извлечены 3 шара разного цвета. Р(А) Ответ Вероятность того, что извлечены три шара разного цвета, равна 0,2727

• Название: Решение а извлечены 3 шара разного цвета. Р(А) Ответ Вероятность того, что извлечены три шара разного цвета, равна 0,2727
• Дата: 22.02.2023
• Размер: 156.5 Kb.
• Имя файла: Теория вероятностей. МУБиНТ. Вариант №34..doc
• Тип: Решение; #950188

Задача №1
В коробке 12 шаров, из которых 3 белых, 4 красных и 5 синих. Случайным образом извлечены три шара. Найти вероятность, того что все 3 шара разного цвета.
Решение:
А – извлечены 3 шара разного цвета.

Р(А) =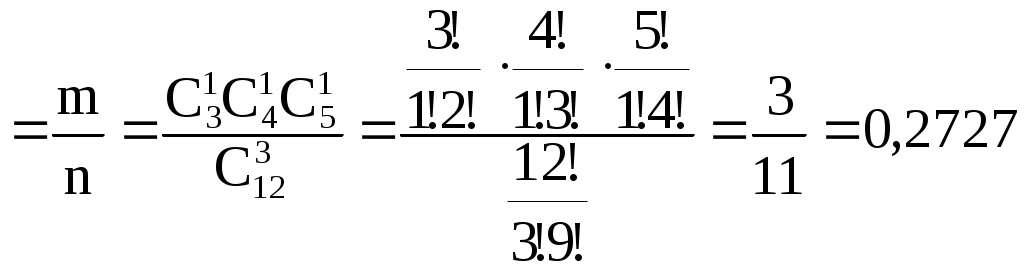
Ответ: Вероятность того, что извлечены три шара разного цвета, равна 0,2727.


Задача №2
Вероятности попадания в мишень при каждом выстреле для стрелков равны соответственно 4/5, 3/4, 2/3. Все трое одновременно выстрелили, после чего обнаружили 2 попадания. Определить вероятность того, что промахнулся третий стрелок.
Решение:
Е – в мишени обнаружили два попадания;

– попал первый и второй стрелок, а третий – промахнулся;

– попал первый и третий стрелок, а второй – промахнулся;

– попал второй и третий стрелок, а первый – промахнулся.

, = 1 – =

, = 1 – =

, = 1 – =

Р( ) = ∙ ∙ =

Р( ) = ∙ ∙ =

Р( ) = ∙ ∙ =

1

1

1

Определим .

Воспользуемся формулой Байеса.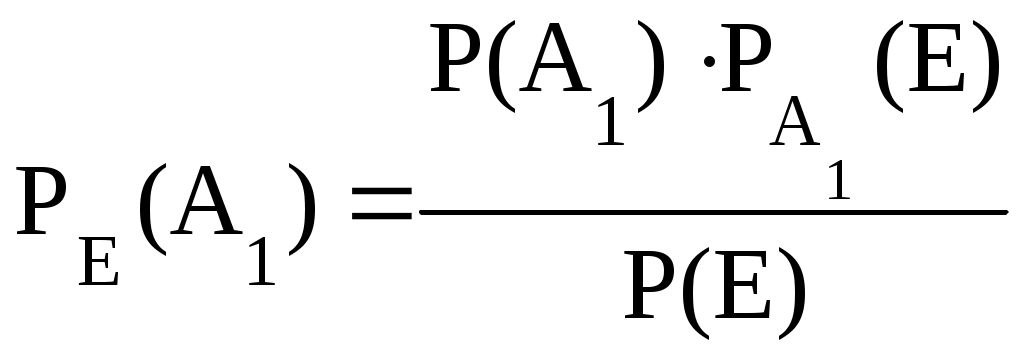



Р(Е) = Р( )∙ + Р( )∙ + Р( )∙

Р(Е) = ∙1 + ∙1 + ∙1 =

Искомая вероятность.

0,4615
Ответ: Все трое стрелков выстрели, после чего обнаружили 2 попадания. Вероятность того, что промахнулся третий стрелок, равна 0,4615.

Задача №3
Если у одной из могил проходящий заглянет в горящие глаза сидящему на кресте коту, то чья-то нечистая рука утащит его под землю. Вероятность того, что глаза у кота будут открыты – 0,7, а вероятность того, что в них кто-то заглянет – 0,9. Найти вероятность того, что под землей окажутся 3 человека из 10 проходивших кладбищем.
Решение:
А – человек окажется под землей.

Р(А) = 0,7∙0,79= 0,63

q = 1 – p = 1 – 0,63 = 0,37

События независимые.

Применим формулу Бернулли.

, где

= 0,0285
Ответ: Вероятность того, что под землей окажутся 3 человека из 10 проходивших кладбищем, равна 0,0285.
Задача №4
Вероятность попадания при каждом выстреле равна 0,4. За каждое попадание он получает 5 очков, при промахе очков не начисляют. Составит закон распределения числа очков, полученным стрелком за три выстрела. Вычислить математическое ожидание этой СВ.
Решение:
1. Случайная величина Х – число полученных очков: = 0, = 5, = 10, = 15.

Определим соответствующие вероятности.

р = 0,4, = 1 – р = 1 – 0,4 = 0,6

Р(х = 0) = ∙ ∙ = 0,6∙0,6∙0,6 = 0,216

Р(х = 5) = р∙ ∙ + ∙р∙ + ∙ ∙р = 0,4∙0,6∙0,6 + 0,6∙0,4∙0,6 +

+ 0,6∙0,6∙0,4 = 0,432

Р(х = 10) = р∙р∙ + р∙ ∙р+ ∙р∙р= 0,4∙0,4∙0,6 + 0,4∙0,6∙0,4 +

+ 0,6∙0,4∙0,4 = 0,288

Р(х = 15) = р∙р∙р= 0,4∙0,4∙0,4 = 0,064

Искомый закон распределения:

	0	5	10	15
	0,216	0,432	0,288	0,064

2. Определим математическое ожидание.



M(Х) = 0∙0,216 + 5∙0,432 + 10∙0,288 + 15∙0,064 = 6
Ответ: 6.
Задача №5
Случайная величина Х распределена по нормальному закону с математическим ожиданием 15 и дисперсией 900. Вычислить вероятность попадания случайной величины в интервал (50; 90).
Решение:
Вероятность определим по формуле:



а = 15, 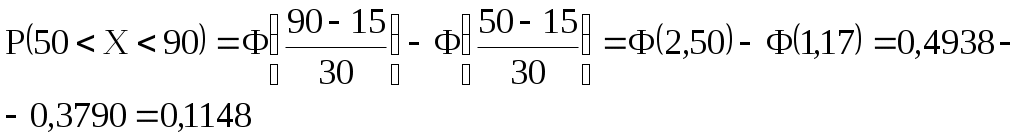= 30


Ответ:

Список литературы
1. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. пособие для студентов вузов. Изд. 5-е, стер. – М.: Высш. шк., 2001. – 400с.: ил.

2. Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник для вузов. – 2-е изд., перераб. и доп. – М.: ЮНИТИ-ДАНА, 2006. – 573с.