термодинамика. Решение а Молярная теплоемкость газа По первому началу термодинамики Внутренняя энергия газа
 Скачать 0.49 Mb. Скачать 0.49 Mb.
|
|
Решение задач, контрольных работ по физике. Вариант 2 Имеется идеальный газ, молярная теплоемкость Решение: а) Молярная теплоемкость газа: По первому началу термодинамики Внутренняя энергия газа: Тогда изменение внутренней энергии газа: Кроме того, Поскольку, по условию, то, Согласно уравнению Менделеева – Клапейрона С учетом того, что по условию Тогда Следовательно, б) выше получено соотношение Тогда Поскольку 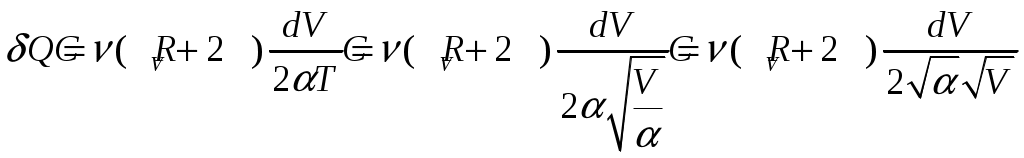 Тогда при расширении газа сообщенное ему количество теплоты: 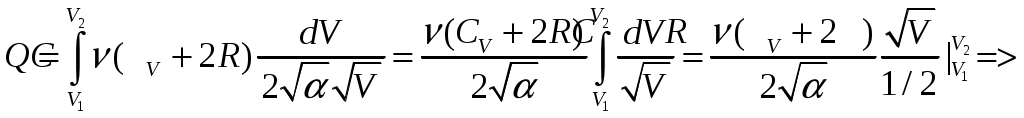 Двухатомный идеальный газ занимает объем Решение: 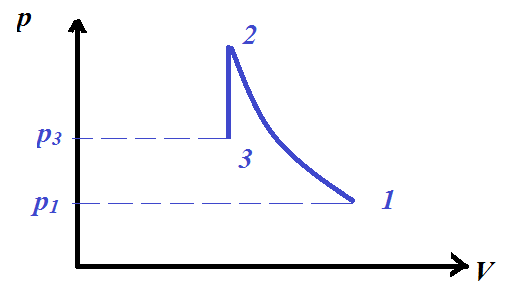 а) Уравнение адиабаты: Постоянная адиабаты Согласно уравнению Менделеева-Клапейрона можем записать: Здесь мы учли, что Из уравнений (2) получаем: Из (1) и (3) получаем: 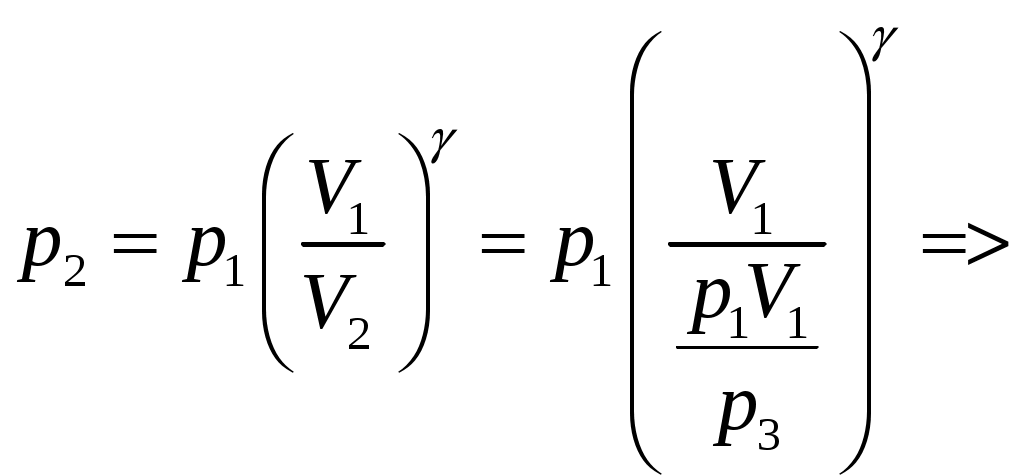 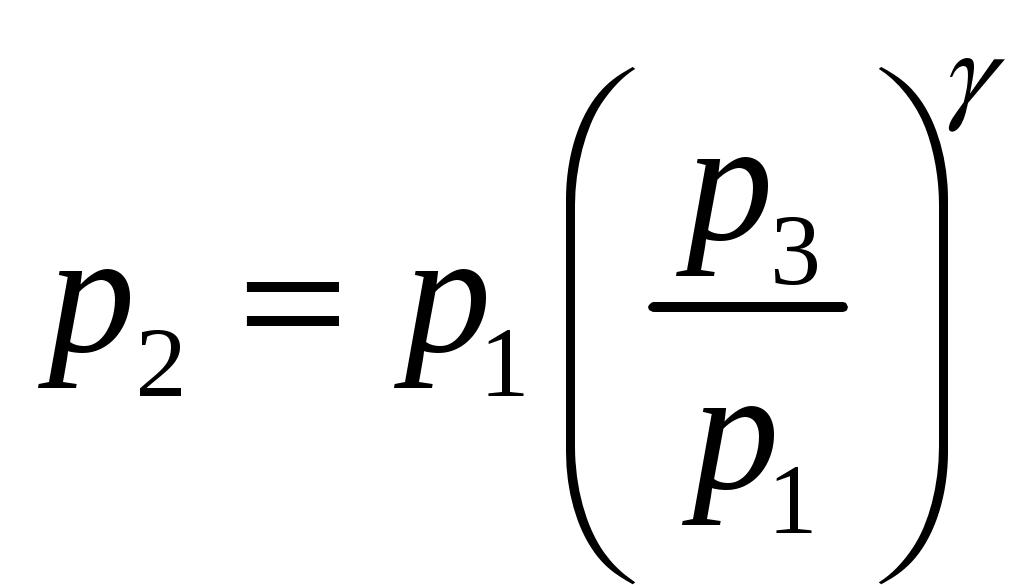 (4) (4)б) Работа газа: В адиабатическом процессе При изохорном процессе изменение объема равно 0, поэтому работа также равна нулю: С учетом (3-4): 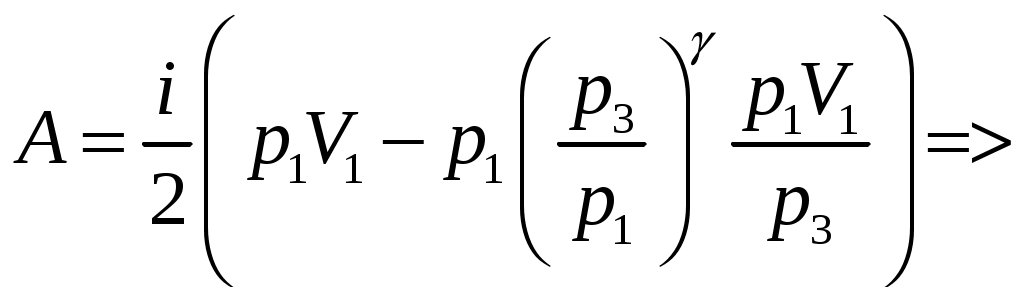 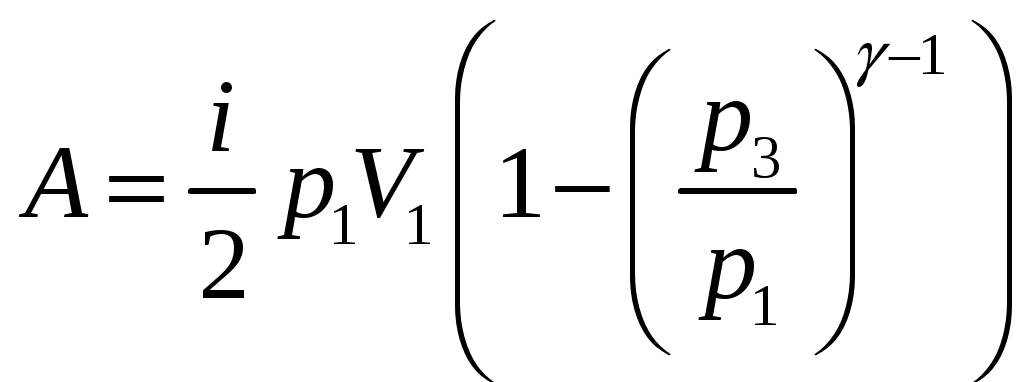 (6) (6)Внутренняя энергия газа: Тогда изменение внутренней энергии газа в результате всего процесса: По условию, Количество теплоты, полученное в процессе 1-2, равно 0, поскольку процесс адиабатический: Количество теплоты, полученное в процессе 2-3 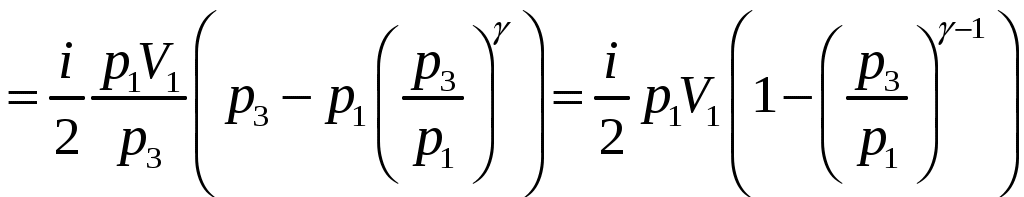 В итоге 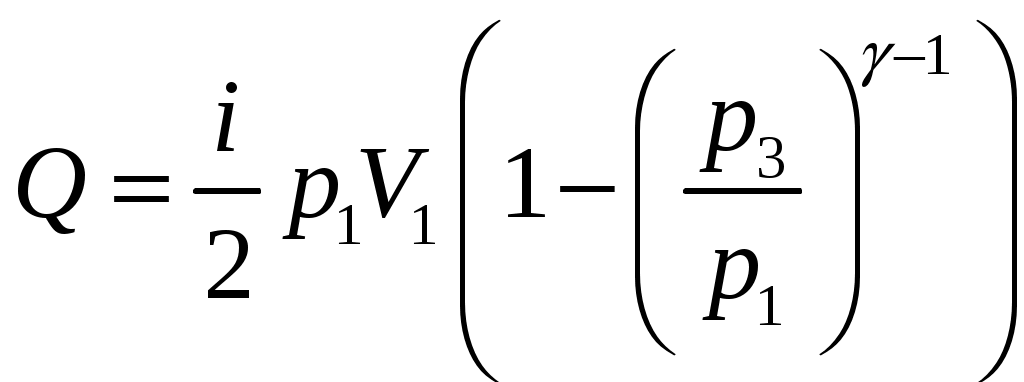 (8) (8)Видно, что правая часть (8) совпадает с (6), т.е. в рассматриваемом процессе А=Q. Произведем расчет согласно формулам (3-4), (6-8): 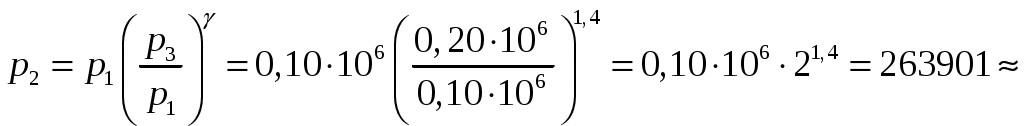 0,26 МПа 0,26 МПа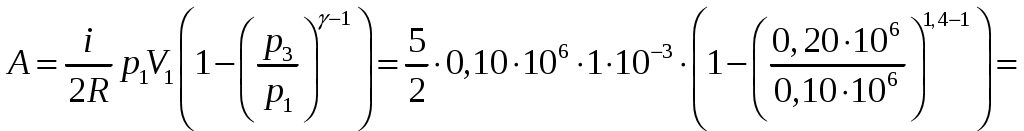 Азот массой 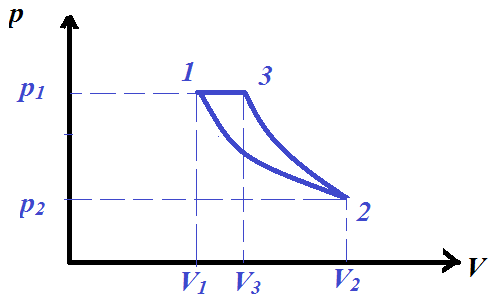 Работа газа: В изотермическом процессе: Здесь n=3, согласно условию. Согласно уравнению Менделеева - Клапейрона можем записать: Здесь мы учли, что Уравнение адиабаты: Учитывая Из (5) получаем: 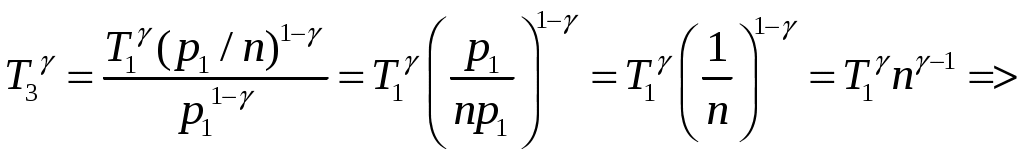 Постоянная адиабаты В адиабатическом процессе: 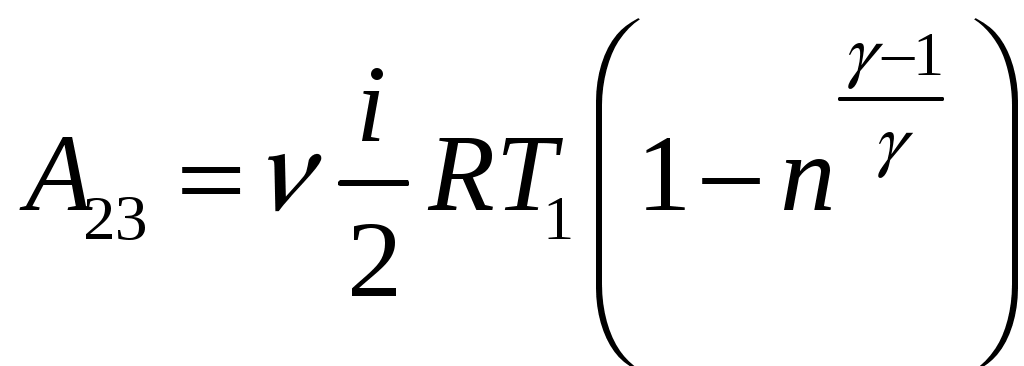 (7) (7)В изобарном процессе работа: 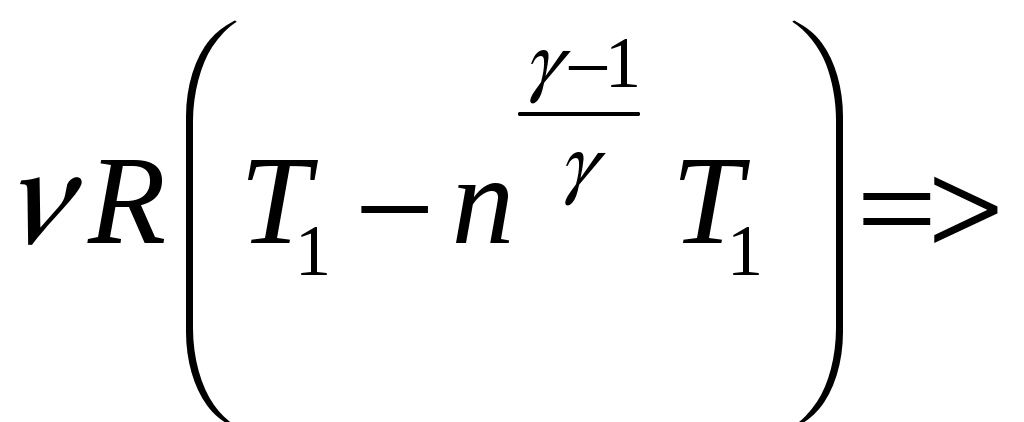 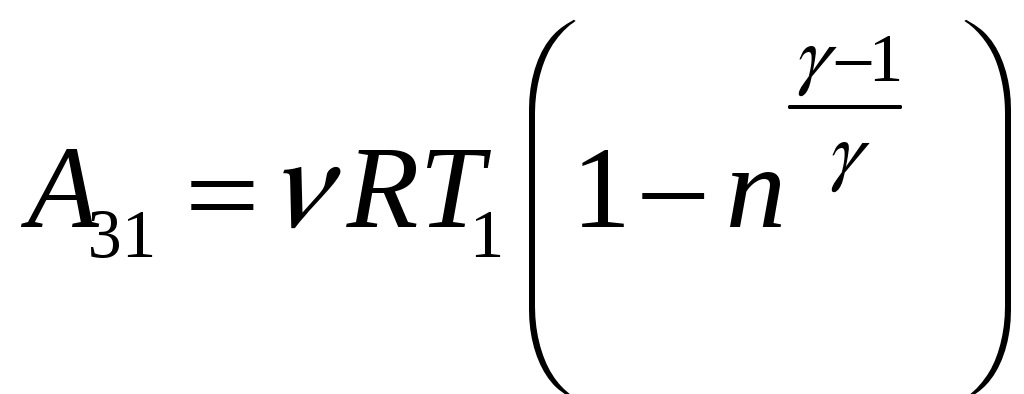 (8) (8)Тогда из (1), (2), (7), (8): 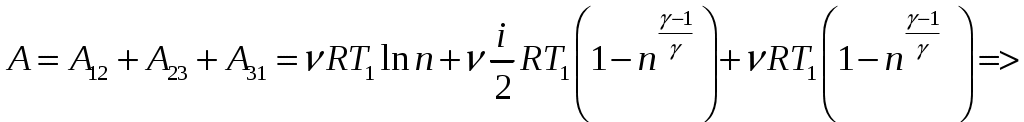 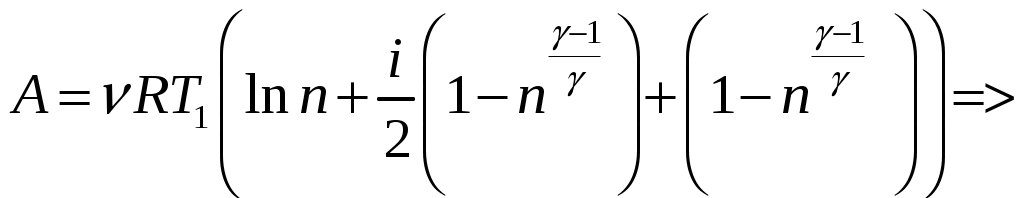 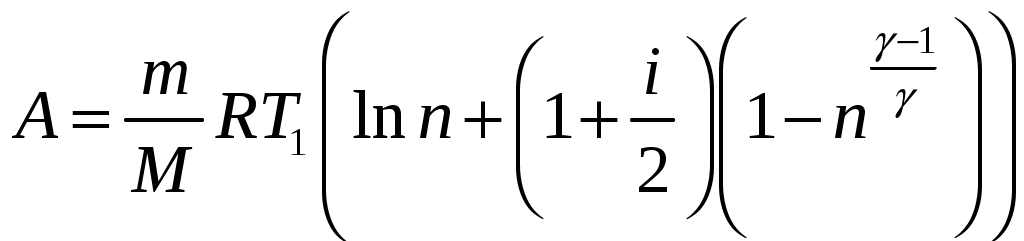 (9) (9)Холодильный коэффициент равен отношению количества теплоты, которая передается газу за цикл, к работе внешних сил, совершенной за цикл. Работа внешних сил равна работе газа с обратным знаком: ‑A. Найдем количество теплоты, переданное газу. В данном цикле теплота передается газу на этапе изотермического расширения (в адиабатическом процессе теплота не передается и не отнимается, на этапе изобарного сжатия теплота отбирается от газа). По первому началу термодинамики В изотермическом процессе Следовательно, Тогда холодильный коэффициент 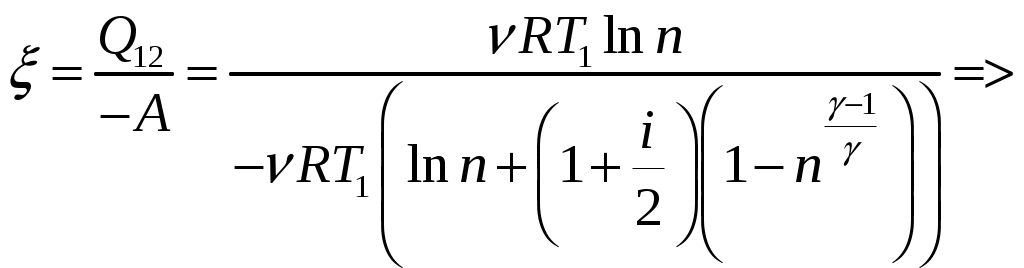 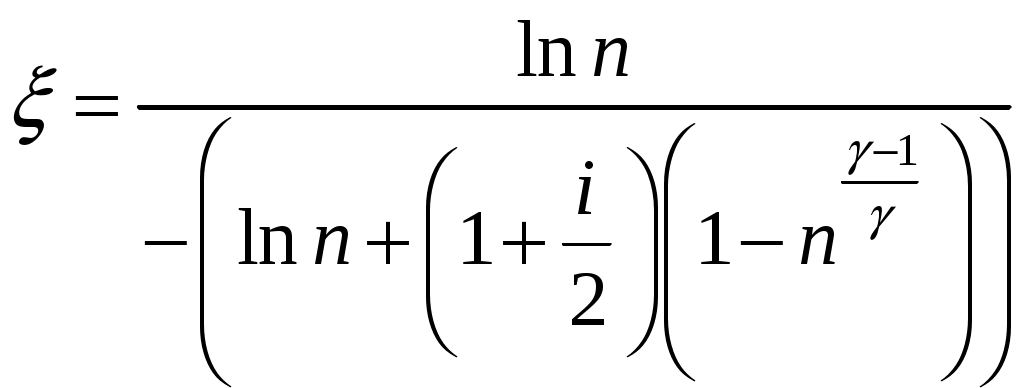 (10) (10)Произведем расчет по (9-10): 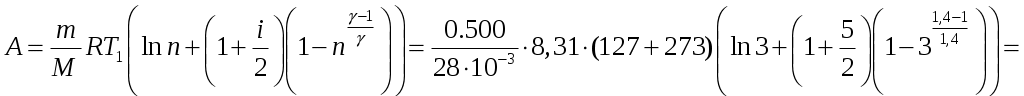 ‑11395 Дж ‑11395 Дж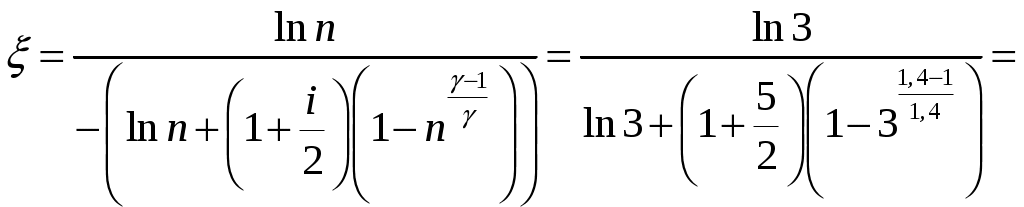 5,7 5,7Найти приращение энтропии алюминиевого бруска массы Приращение энтропии: Тогда при изменении температуры от Т1 до Т2: 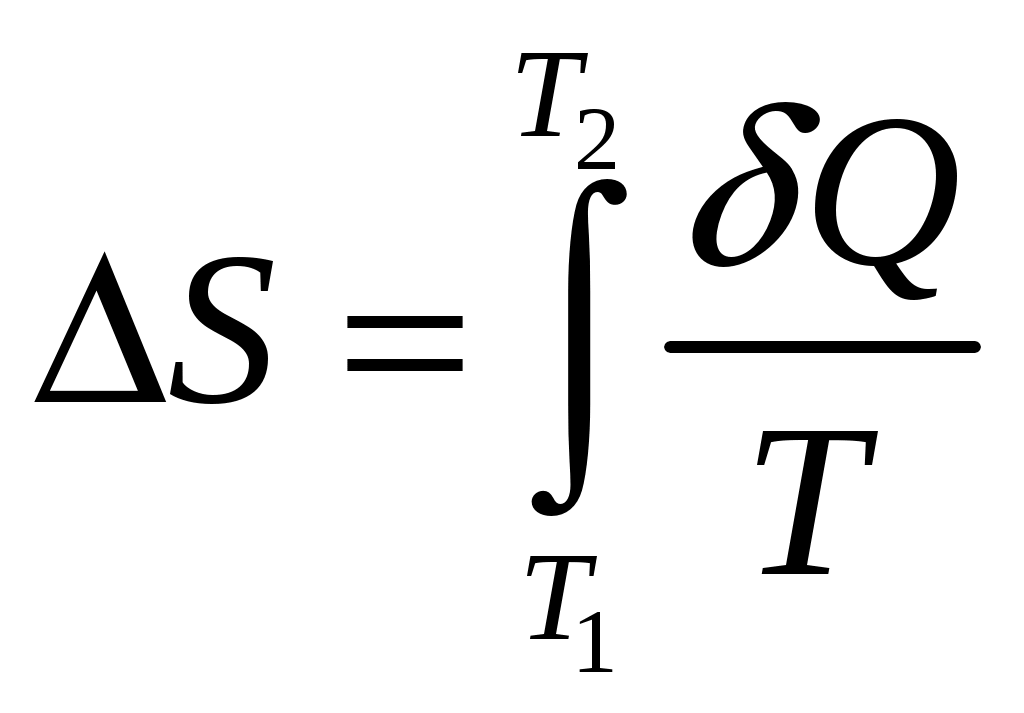 Для изменения температуры бруска на dT ему следует сообщить количество теплоты, равное Тогда 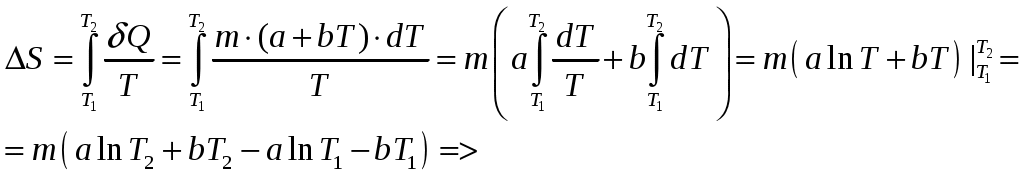 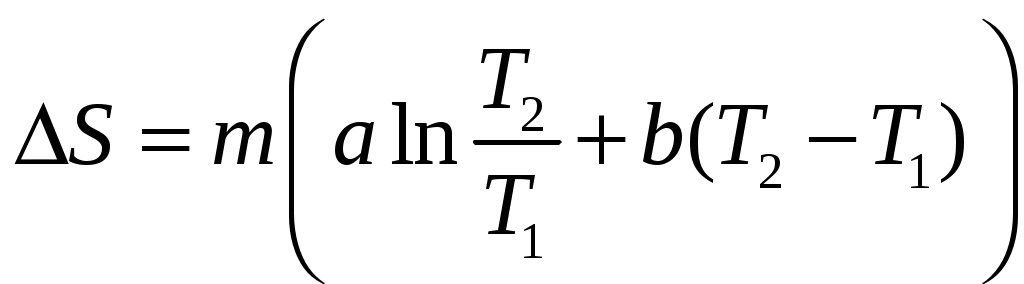 Произведем расчет: Термодинамический потенциал a) Учтем известные из термодинамики соотношения Тогда 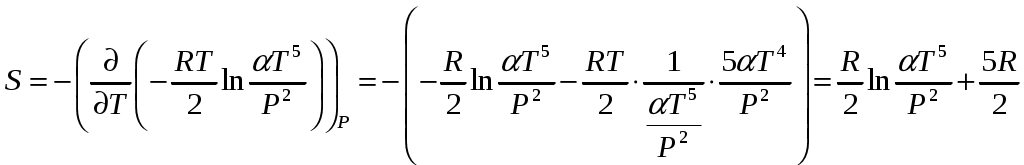 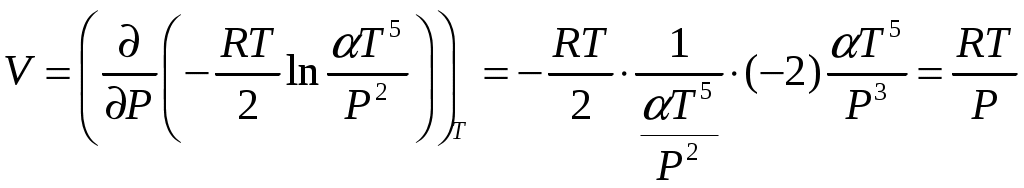 Теплоемкость: 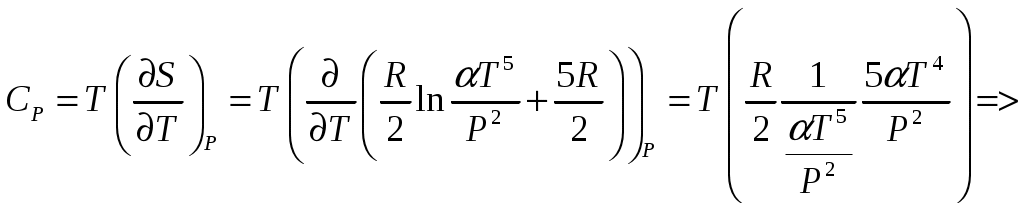 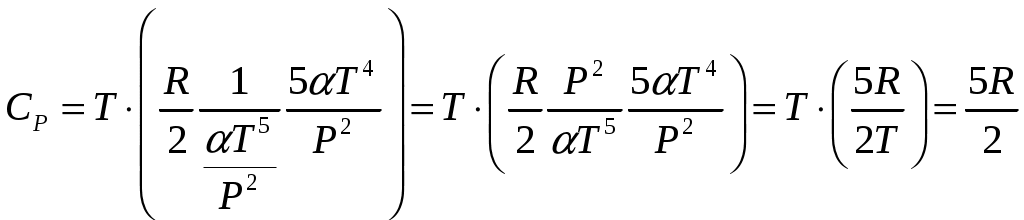 б) Связь потенциала Гиббса G и внутренней энергии: Из выражения для S имеем: Получаем для внутренней энергии Из выражения для V имеем: Тогда На какой высоте Барометрическая формула для плотности воздуха: Отсюда для Учитывая, что молярная масса воздуха М=0,029 кг/моль, получаем Коэффициент диффузии кислорода при Коэффициент диффузии: Здесь Среднеквадратичная скорость Здесь d – диаметр молекулы, n – концентрация молекул. Тогда Поскольку давление газа То Произведем расчет 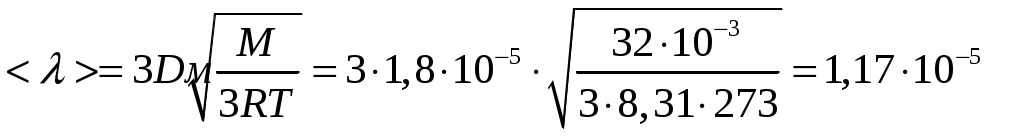 Для определения постоянных Ван-дер-Ваальса некоторое количество газа, занимающего при Уравнение газа Ван-дер-Ваальса: 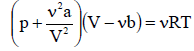 Получаем: 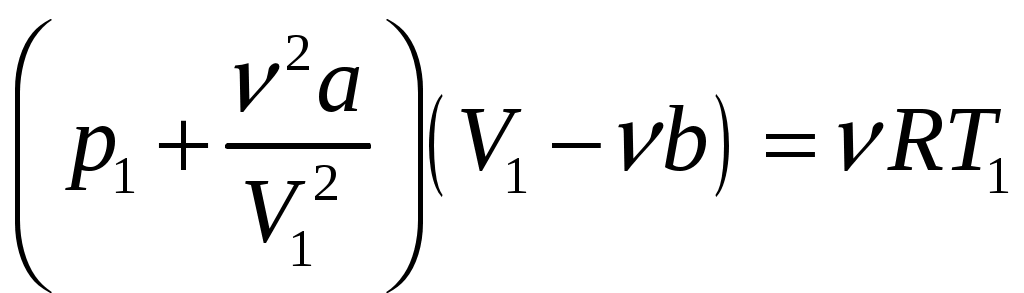 (1) (1)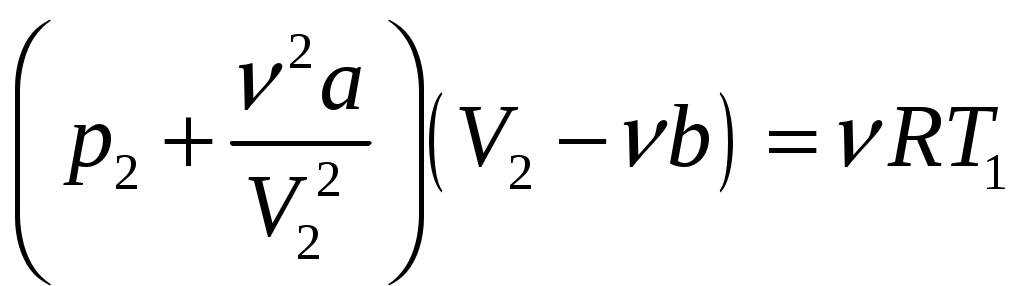 (2) (2)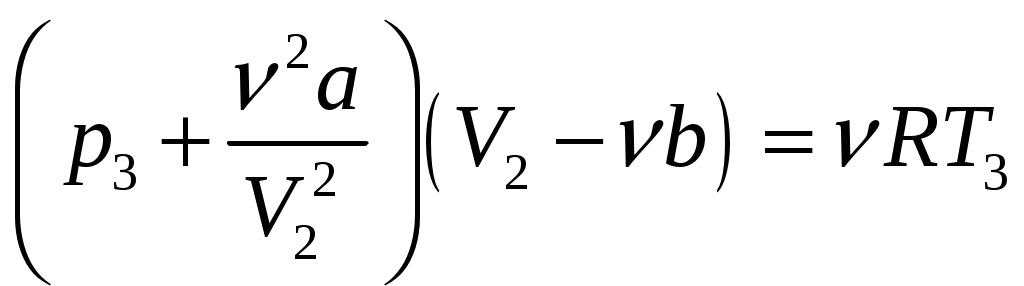 (3) (3)Решение этих уравнений в общем виде весьма громоздко. Для упрощения решения подставим численные значения. Получаем: Раскрывая скобки, получим: Вычитая из первого полученного уравнения (7) второе (8), получаем: Вычитая из уравнения (8) уравнение (9), получаем: Из (11) получаем: Подставляя (12) в (11), получаем: Выразим а из (13): Подставим формулы для ν (12) и для а (14) в (7): + + Домножая на (1+10000b), получим: Приводя подобные слагаемые, получаем: Отсюда Окончательно Подставляя (16) в (14), получаем: В итоге имеем: а≈0,149 м3·Па/моль2 b≈3,32•10‑5 м3/моль |
