32 вар. 32 вариант 3 и 4 задача. Решение а. Найдем ту часть дохода, которую получит 10% наиболее низкооплачиваемого населения
 Скачать 202.78 Kb. Скачать 202.78 Kb.
|
|
Задача 3. Кривые Лоренца распределения дохода в некоторых странах могут быть заданы уравнениями: а) 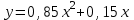 ; ;б) 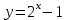 ; ;в) 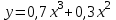 . .Какую часть дохода получат 10% наиболее низкооплачиваемого населения? Вычислить коэффициенты Джини для этих стран. Решение: а) 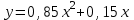 . .Найдем ту часть дохода, которую получит 10% наиболее низкооплачиваемого населения: 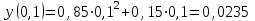 . .Следовательно, искомая часть дохода равна 2,35%. Построим кривую Лоренца и линию абсолютного равенства (прямая 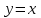 ): ):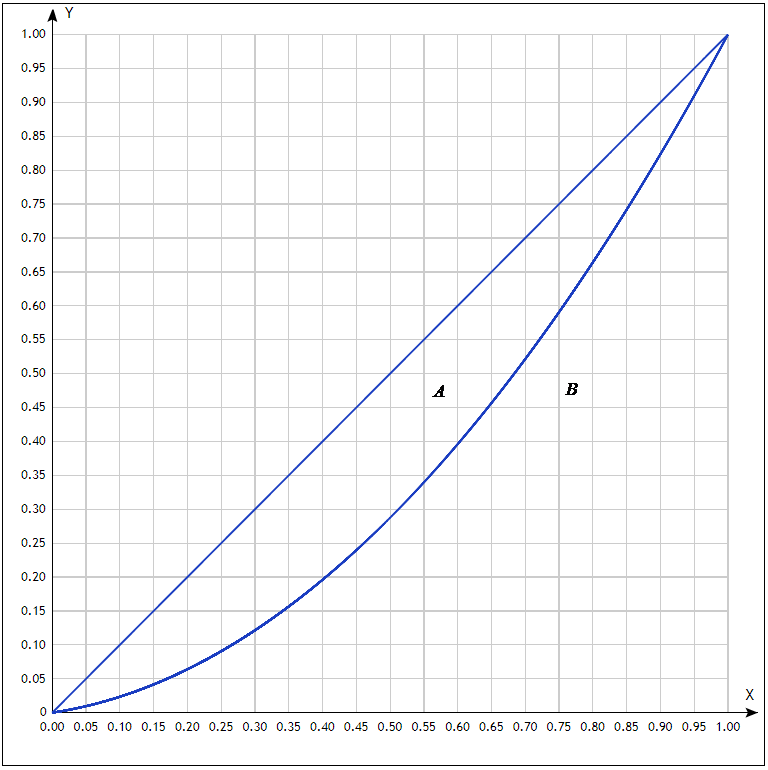 Коэффициент Джинни определяется формулой: 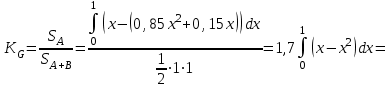 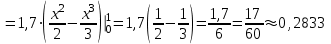 . .б) 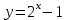 . .Найдем ту часть дохода, которую получит 10% наиболее низкооплачиваемого населения: 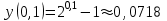 . .Следовательно, искомая часть дохода равна 7,18%. Построим кривую Лоренца и линию абсолютного равенства (прямая 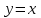 ): ):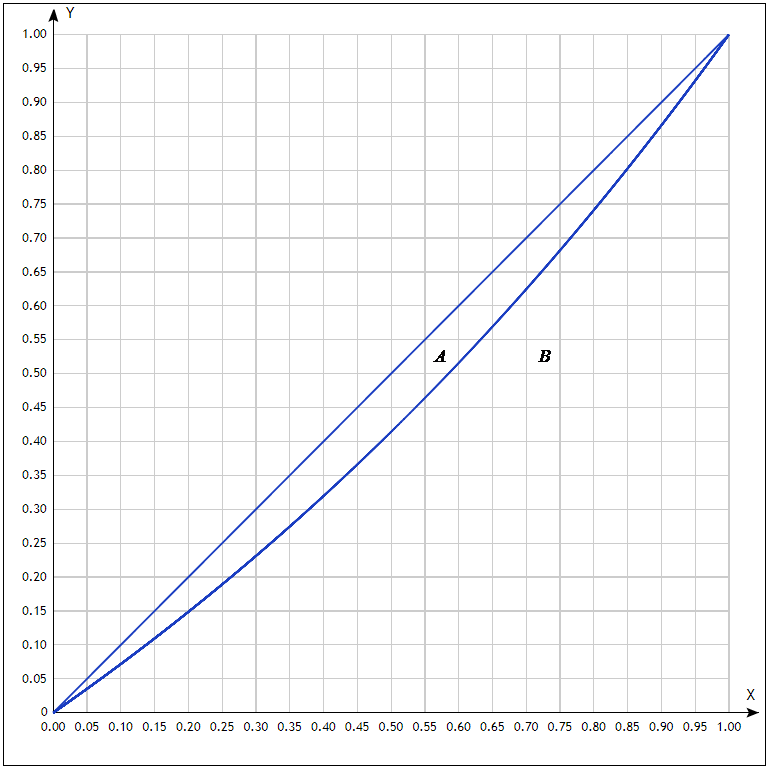 Коэффициент Джинни определяется формулой: 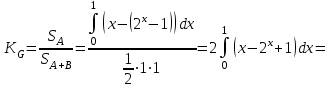 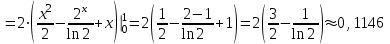 . .в) 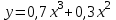 . .Найдем ту часть дохода, которую получит 10% наиболее низкооплачиваемого населения: 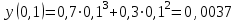 . .Следовательно, искомая часть дохода равна 0,37%. Построим кривую Лоренца и линию абсолютного равенства (прямая 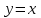 ): ):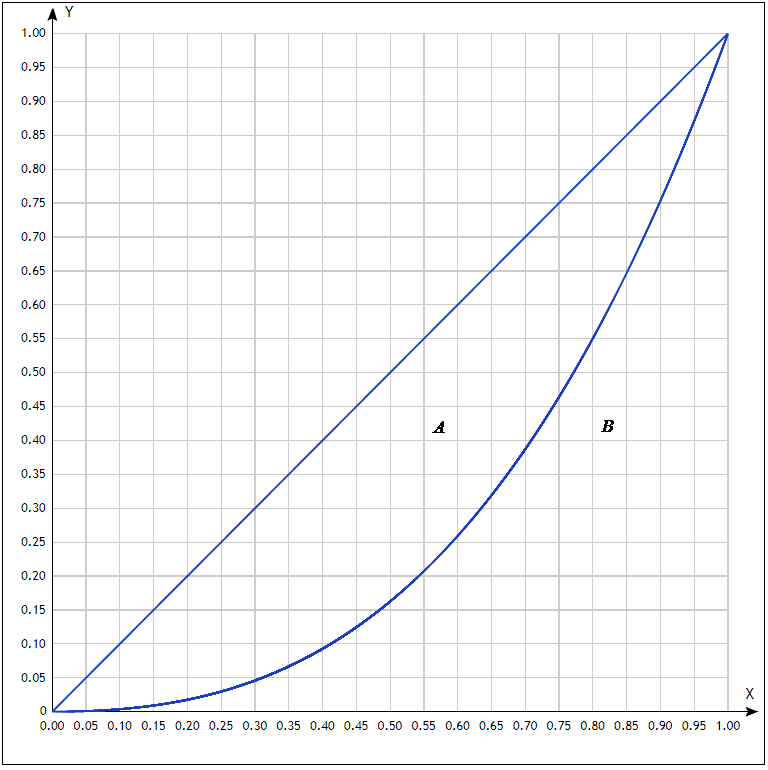 Коэффициент Джинни определяется формулой: 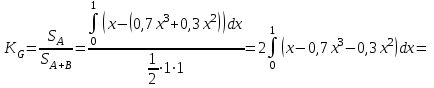 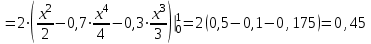 . .Задача 4. Найти функцию спроса, если известно значение цены 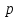 при некотором спросе при некотором спросе 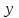 и эластичность имеет следующий вид: и эластичность имеет следующий вид:а) 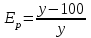 , , 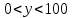 , , 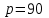 при при 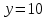 ; ;б) 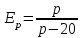 , , 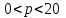 , ,  при при 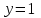 . .Решение: а) 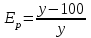 , , 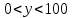 , , 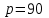 при при 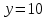 . .Составим и решим задачу Коши, используя определение эластичности: 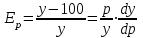 , , 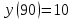 . .Тогда получаем: 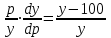 , , 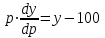 , , 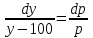 , ,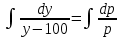 , , 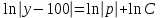 , , 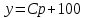 . .Константу 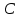 определим из начального условия: определим из начального условия: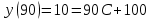 , , 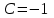 . .Тогда получаем: 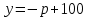 - искомая функция спроса, удовлетворяющая начальному условию. - искомая функция спроса, удовлетворяющая начальному условию.б) 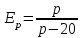 , , 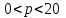 , ,  при при 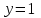 . .Составим и решим задачу Коши, используя определение эластичности: 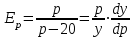 , , 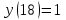 . .Тогда получаем: 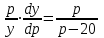 , , 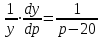 , , 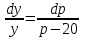 , ,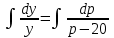 , , 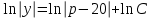 , , 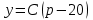 . .Константу 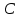 определим из начального условия: определим из начального условия: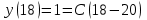 , , 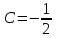 . .Тогда получаем: 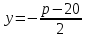 - искомая функция спроса, удовлетворяющая начальному условию. - искомая функция спроса, удовлетворяющая начальному условию. |
