Логистика снабжения. Решение а) Оптимальное количество закупаемых автомобилей в течение месяца вычислим по следующей формуле Ко v 2 С3ПИ (шт.)
 Скачать 51.7 Kb. Скачать 51.7 Kb.
|
|
Задание 18. В ячейках матрицы А1В]С1-А2В2С2-анализа указано по одной из позиций торгового ассортимента, входящего в данную группу (указан код позиции). AjBjCj-анализ выполнен по признаку доли позиции в общей реализации. А2В2С2-анализ выполнен по признаку доли позиции в общей встречаемости в заказах клиентов. Наиболее безболезненно можно удалить из ассортимента позицию а) 125 б) 955 в) 270 8 г) 206 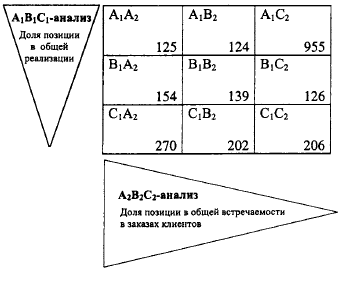 Наиболее безболезненно можно удалить из ассортимента позицию 206 Задание 19. В ячейках матрицы А 1В 1 С1 -А2В2С2-анализа указано по одной из позиций торгового ассортимента, входящего в данную группу (указан код позиции). А1В 1 С 1 -анализ выполнен по признаку доли позиции в общей реализации. А2В2С2-анализ выполнен по признаку ДОЛИ позиции в общей встречаемости в заказах клиентов. 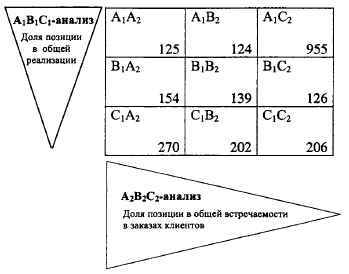 Только при наличии заказа покупателя целесообразно закупать 955 Задача 1 В течение месяца компании требуется 3 марки автомобилей для организации продаж. В течение данного периода времени по каждому виду определите: а) оптимальное количество закупаемых автомобилей; б) оптимальное число заказов; в) оптимальные переменные издержки за хранение запасов; г) разницу между переменными издержками по оптимальному варианту и случаем, когда покупка всей партии проводится в первый день месяца. Исходные данные: • потребность в автомобилях в течение месяца (шт.) – 1) 67; 2) 37; 3) 29; • стоимость заказа партии товара (долл. США) – 1) 217; 2) 318; 3) 338; • издержки хранения единицы товара в течение месяца (долл. США) - 1) 49; 2) 67; 3) 91. Решение: а) Оптимальное количество закупаемых автомобилей в течение месяца вычислим по следующей формуле: Ко = v 2 С3П/И (шт.), где С3 - стоимость заказа партии товара (долл. США.); П - потребность в автомобилях в течение месяца (шт.); И - издержки хранения единицы товара в течение месяца (долл. США.). Подставив в формулу исходные данные, для первой марки автомобилей получаем К01 = v2*217*67/49 = 24 шт. Для второй марки автомобилей получаем К02 = v2*318*37/67 = 19 шт. Для третьей марки автомобилей получаем К03 = v2*338*29/91 = 15 шт. б) Оптимальное число заказов автомобилей в течение месяца вычислим по следующей формуле Ч = v ПИ/2С3. Подставив в формулу исходные данные, для первой марки автомобилей получаем Ч1 = v67*49/2*217 = 3 заказа. Для второй марки автомобилей получаем Ч2 = v37*67/2*318 = 2 заказа. Для третьей марки автомобилей получаем Ч3 = v29*91/2*338 = 2 заказа. в) Оптимальные переменные издержки за хранение запасов в течение месяца вычислим по следующей формуле: Ио = v2ПИС3. Подставив в формулу исходные данные, для первой марки автомобилей получаем Ио1 = v2*67*49*217 = 1193,66 долл. США. Для второй марки автомобилей получаем И о2 = v2*37*67*318 = 1255,64 долл. США. Для третьей марки автомобилей получаем И о3 = v2*29*91*338 = 1335,65 долл. США. г) Разницу между переменными издержками по оптимальному варианту и случаем, когда покупка всей партии проводится в первый день месяца, вычислим по следующей формуле: Р = ИП/2 + С3 - Ио. Подставив в формулу данные, для первой марки автомобилей получаем Р1 = 49 * 67/2 + 217 - 1193,66 = 664,84 долл. США. Для второй марки автомобилей получаем Р2 = 67 * 37/2 + 318 - 1255,64 = 301,86 долл. США. Для третьей марки автомобилей получаем Р3 = 91 * 29/2 + 338 - 1335,65 = 321,85 долл. США. Ответ: а) 24 шт.; 19 шт.; 15 шт.; б) 3 раза; 2 раза; 2 раза; в) 1193,66; 1255,64 руб.; 1335,65 долл. США; г) 664,84 руб.; 301,86 руб.; 321,85 долл. США. |
