теория вероятности. КР12. Решение а Суммируя элементы матрицы по строкам и по столбцам, получим соответственно ряды распределений у и Х

• Название: Решение а Суммируя элементы матрицы по строкам и по столбцам, получим соответственно ряды распределений у и Х
• Анкор: теория вероятности
• Дата: 02.07.2022
• Размер: 104 Kb.
• Имя файла: КР12.doc
• Тип: Решение; #622694

1. Дана матрица распределения вероятностей системы (X,Y)

	X
Y	1	2	3
1	0.2500	0.1100	0.1600
2	0.1300	0.2000	0.1500

Найти: а) ряды распределений X и Y; б) m_x; в) m_y; г) D_x; д) D_y; е)cov(X,Y); ж) r_xy, округлить до 0,01; з) ряд распределения Y, если Х=1; и) M[X/Y=1], округлить до 0,01.

Решение:

а)

Суммируя элементы матрицы по строкам и по столбцам, получим соответственно ряды распределений У и Х

Х	1	2	3
рх	0,3800	0,3100	0,3100

У	1	2
ру	0,5200	0,4800

б) m_x = 0.38 + 0.62 + 0.93 = 1.93

в) m_y = 0.52 + 0.96 = 1.48

г)

Х	1	2	3	Dx
рх	0,38	0,31	0,31	0,6851
рхX2	0,38	1.24	2.79	4,41

д)

У	1	2	Dy
ру	0,52	0,48	0,2496
руY2	0,52	1.92	2.44

е) Ковариацию cov(X,Y) находим по формуле



( промежуточные результаты в таблице )

х y	1	2	3
1	0,25 ║ 1	0,11 ║ 2	0,16 ║ 3	0,95
2	0,13 ║ 2	0,2 ║ 4	0,15 ║ 6	1,96

ж) Находим среднеквадратичные отклонения



Коэффициент корреляции

з) Закон распределения У при Х = 1 определяется совокупностью условных вероятностей р(у₁ / Х=1), р(у₂ / Х=1).

Используя данные матрицы распределения вероятностей,

	1	2	3
1	0,25	0,11	0,16
2	0,13	0,2	0,15

находим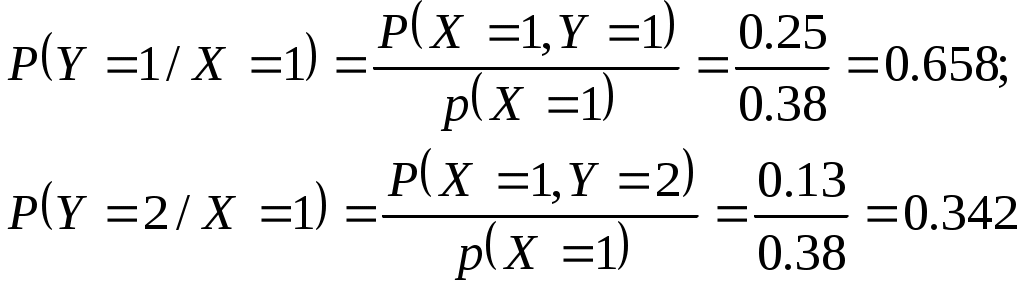



т.е. ряд распределения У при Х = 1

У	1	2
р	0,658	0,342

и)

Ряд распределения Х при У = 1 находим аналогично п. з)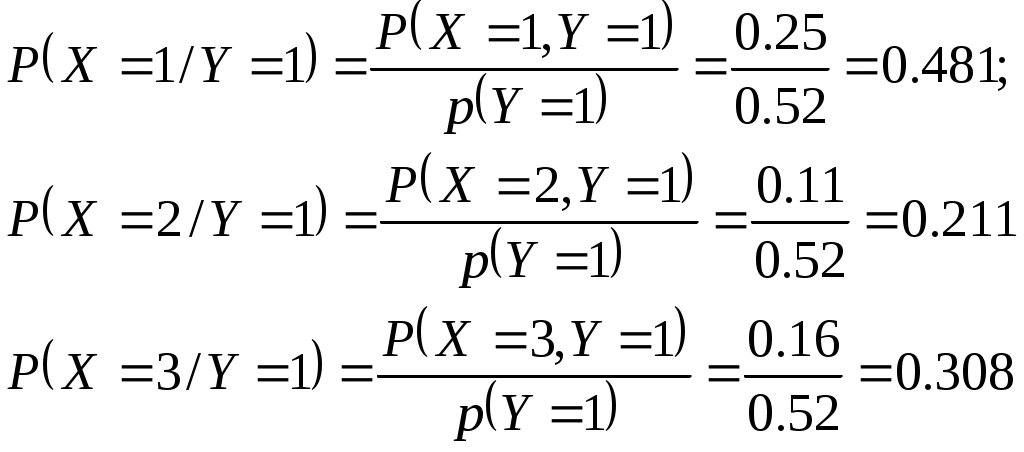



тогда М( Х / У=1 ) = 0,481 + 0,211*2 + 0,308*3 = 1,83
2. Дана плотность распределения вероятностей системы (X,Y):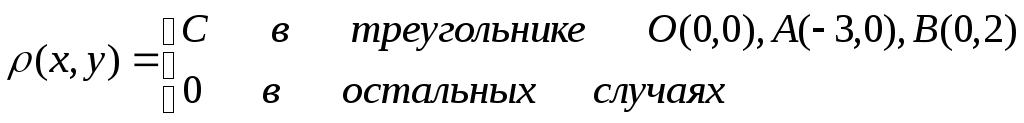



Найти: а) константу C; б) p₁(x), p₂(y); в) m_x; г) m_y; д) D_x; е) D_y; ж) cov(X,Y); з) r_xy; и) F(-1,1); к) М[X/Y=1/2].

Решение:

а)

Вероятность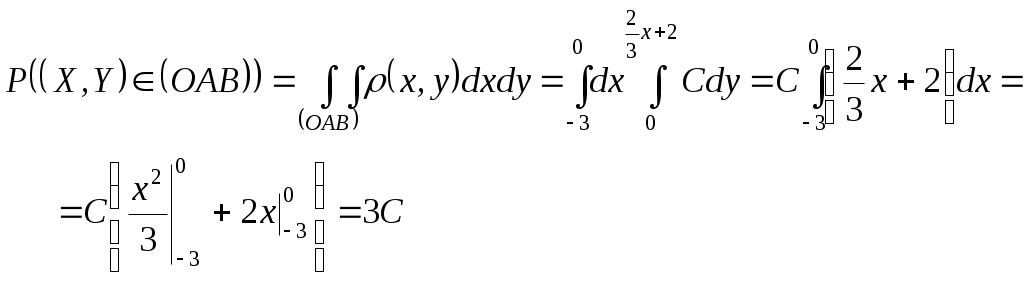



а т.к. – д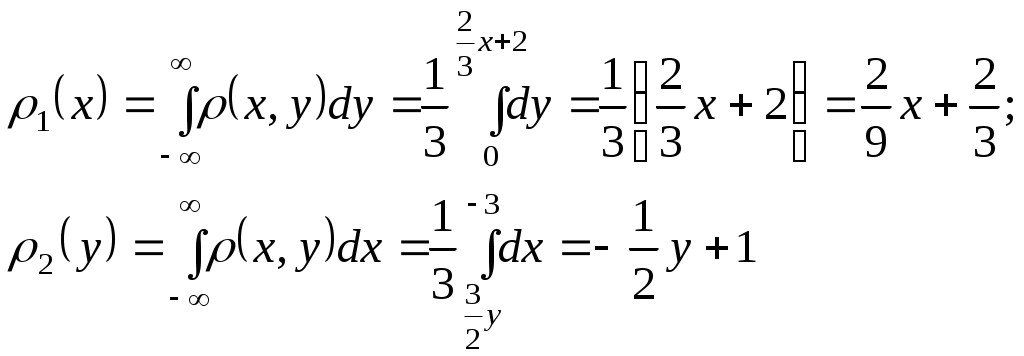остоверное событие, то 3С = 1 => С = ⅓

б)



в)



г)



д)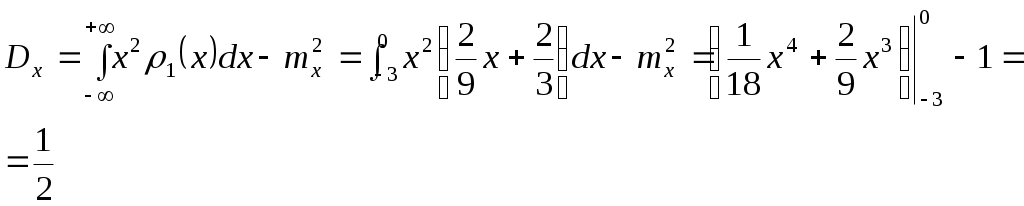



е)



ж)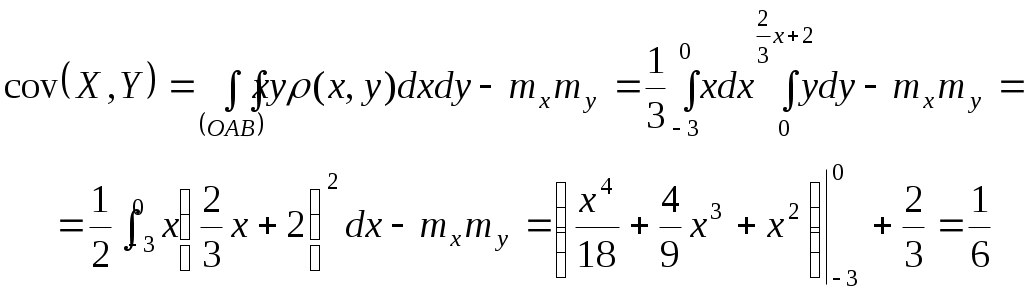



з)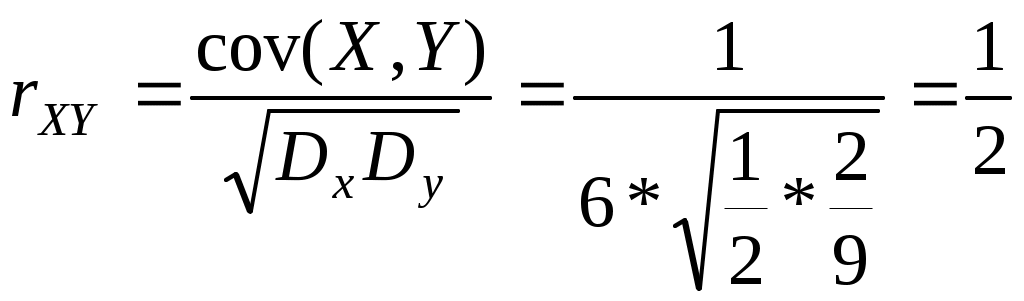



и)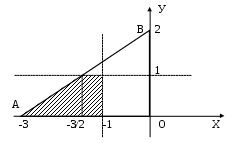




Интегральная функция распределения данной системы равна нулю всюду в

левом нижнем квадранте с центром в т.(-3; 0). Тогда по определению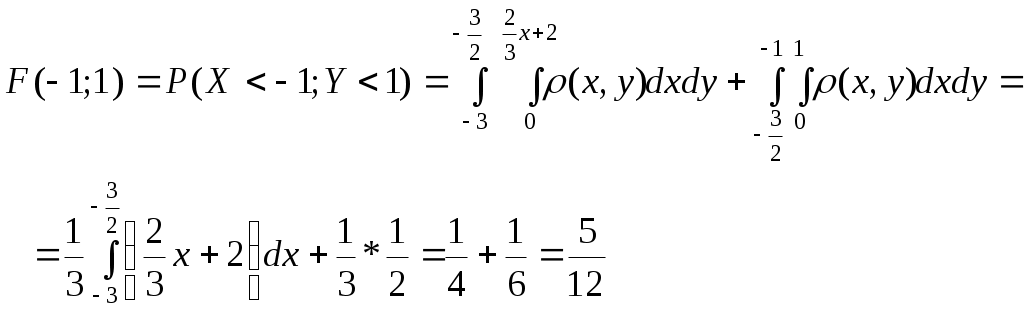



к)

Плотность распределения Х при У = ½ ( х [-9/4; 0] )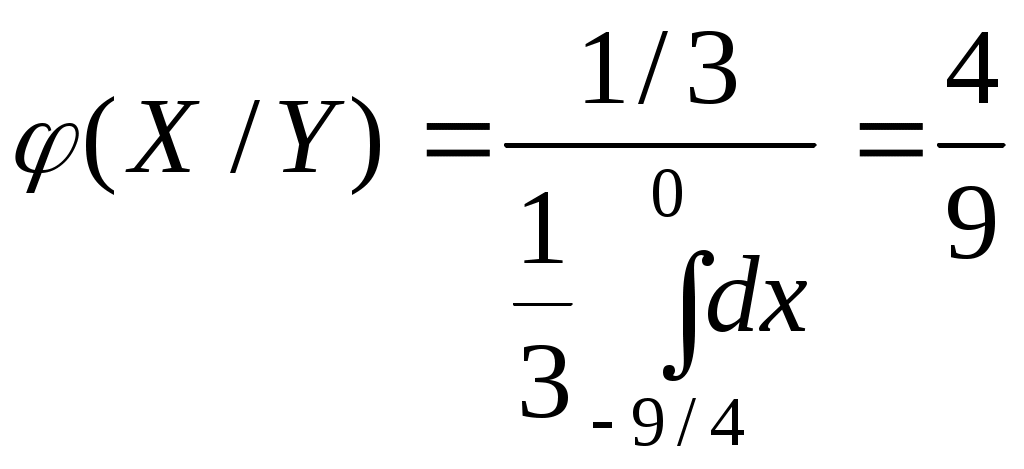



Тогда условное матожидание М(Х |У = ½ )



3. По данным 25 независимых измерений некоторой величины найдено среднее арифметическое результатов измерений и исправленная дисперсия s²=64. Построить доверительный интервал для истинного значения измеряемой величины a с надежностью γ=0,95. В ответ ввести координату правого конца интервала.

Решение:

Истинное значение величины – это её матожидание, доверительный интервал которого с надёжностью 



Для данных n = 25,  = 0.95 по таблицам находим t_ = 2.064.

Тогда

Значит, 31,698 < a < 38,302.