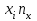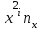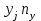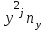анализ данных 1,2 8, — копия. Решение а так как n8000 велико, то по теореме Пуассона, где
 Скачать 147.88 Kb. Скачать 147.88 Kb.
|
|
1) На почту поступило 8000 писем. Вероятность того, что на случайно взятом конверте отсутствует почтовый индекс, равна 0,0005. Найти вероятность того, что почтовый индекс отсутствует: а) на трех конвертах; б) не менее, чем на трех. Решение: а) так как n=8000 велико, то по теореме Пуассона Подставляя n=8000, k=3, р=0,0005 получим б) По теореме Муавра – Лапласа для а=3£x (b=8000) при больших n имеем: По таблице находим Итак, Ответ: а) 0,19537; б) 0,69151. 2)Вероятность поражения цели при одном выстреле равна 0,4. Было произведено 600 выстрелов. Найти: а) границы в которые с вероятностью 0,9949 будет заключено число попаданий в цель; б) число выстрелов, которые надо произвести по мишени, чтобы с вероятностью 0,9949 можно было ожидать, что отклонение частости попадания при одном выстреле от его вероятности будет меньше 0,05 (по абсолютной величине). Решение: n =600 p=0,4 q=1-p=1-0,4=0,6 а) —— = t npq ___ = tnpq P=(m-np ) = Ф ( ——— ) =0,9949 npq По таблице Ф(х) находим такое t, что Ф(t) = 0,9949 t=2,8 =2,8600*0,4*0,6 = 2,8*12=33,6 m1= np+=600*0,4+33,6=273,6 m2= np-=600*0,4-33,6=206,4 P(206,4m273,6) б) 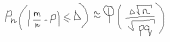 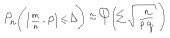 По таблице Ф(х) находим такое t, что Ф(t) = 0,9949 t=2,8 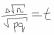 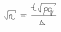 n=2,8²*0,4*0,6/0,005²=1,8816/0,0025=752,64753 Ответ: надо произвести 753 выстрела. 8) Имеются следующие выборочные данные о рыночной стоимости квартир 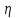 (тыс. у.е.) и их общей площади (тыс. у.е.) и их общей площади 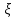 (кв. м.) (кв. м.)
Необходимо: 1. Вычислить групповые средние 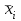 и и 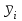 , и построить эмпирические линии регрессии. , и построить эмпирические линии регрессии.2. Предполагая, что между переменными 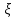 и и 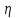 существует линейная корреляционная зависимость: существует линейная корреляционная зависимость:а) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений; б) вычислить коэффициент корреляции; на уровне значимости α = 0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными 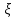 и и 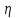 ; ;в) используя соответствующее уравнение регрессии, оценить стоимость квартиры общей площадью 75 кв. м. Решение: Вычислим групповые средние х i и у j , построим эмпирические линии регрессии. Для каждого значения 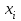 , т.е. для каждой строки корреляционной таблицы вычислим групповые средние , т.е. для каждой строки корреляционной таблицы вычислим групповые средние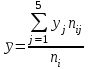 , где , где 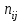 - частоты пар ( - частоты пар (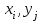 ) и ) и 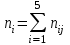 . .Вычисленные групповые средние 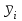 поместим в последнем столбце корреляционной таблицы и изобразим графически в виде ломаной, называемой эмпирической линией регрессии Y по X. поместим в последнем столбце корреляционной таблицы и изобразим графически в виде ломаной, называемой эмпирической линией регрессии Y по X.Аналогично для каждого значения 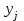 по формуле по формуле 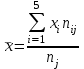 , где , где 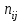 - частоты пар ( - частоты пар (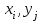 ) и ) и 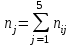 . .Вычисленные групповые средние 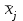 поместим в последней строке корреляционной таблицы и изобразим графически в виде ломаной, называемой эмпирической линией регрессии поместим в последней строке корреляционной таблицы и изобразим графически в виде ломаной, называемой эмпирической линией регрессии 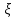 и и 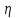 . .
Где, 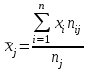 , , 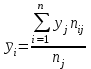 . .Эмпирическая линия регрессии 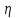 по по 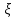 : :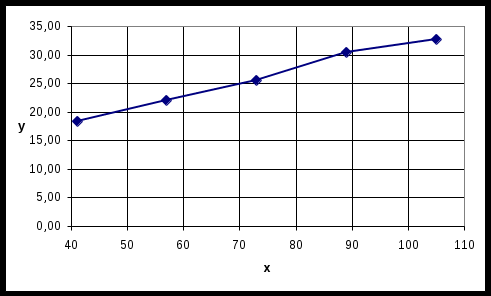 Эмпирическая линия регрессии 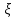 по по 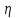 : :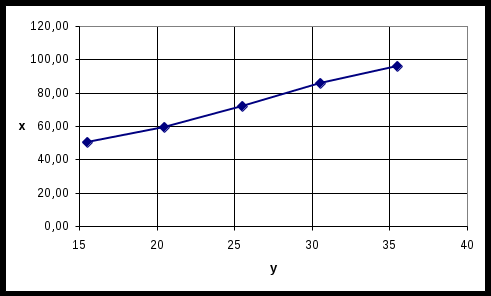 2) Предполагая, что между переменными 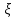 и и 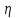 существует линейная корреляционная зависимость: а) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений; существует линейная корреляционная зависимость: а) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений;Вычислим необходимые суммы: 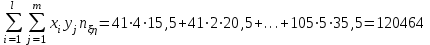 ; ;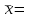 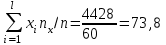 ; ;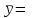 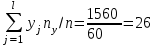 ; ;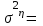 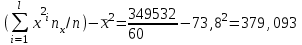 ; ;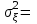 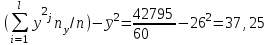 ; ;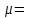 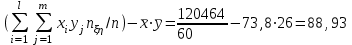 Итак, уравнение регрессии 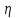 по по 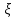 : : 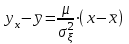 . .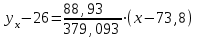 ; ; 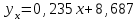 . .Итак, уравнение регрессии 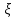 по по 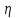 : : 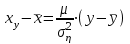 . .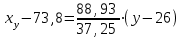 ; ; 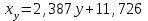 . .Из первого уравнения регрессии 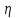 по по 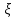 следует, что при увеличении рыночной стоимости квартир на 1 тыс. у. е. их общая площадь увеличивается на 0,235 м2. следует, что при увеличении рыночной стоимости квартир на 1 тыс. у. е. их общая площадь увеличивается на 0,235 м2.Из второго уравнения регрессии 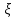 по по 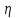 следует, что при увеличении площади квартир на 1 м2 увеличивается рыночная стоимость квартир на 2,387 тыс. у. е. следует, что при увеличении площади квартир на 1 м2 увеличивается рыночная стоимость квартир на 2,387 тыс. у. е.Построим графики уравнений регрессии на одном чертеже с эмпирическими линиями регрессии: 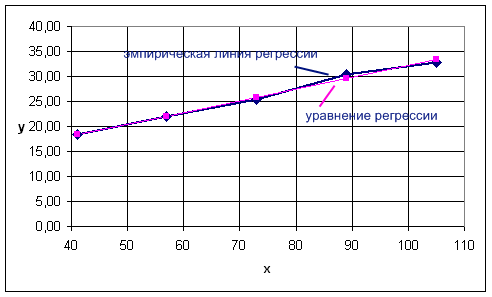 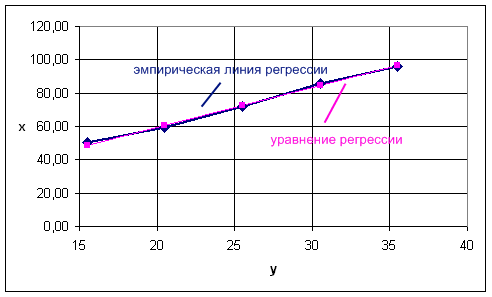 б) вычислить коэффициент корреляции, на уровне 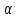 = 0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными = 0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными 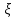 и и 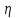 . .Вычислим коэффициент корреляции по формуле: 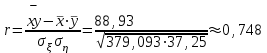 . .Связь между переменными 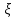 и и 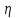 прямая, т.к. прямая, т.к. 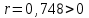 и достаточно тесная ( и достаточно тесная (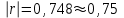 достаточно близок к 1). достаточно близок к 1). На уровне значимости 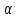 = 0,05 оценить значимость коэффициента корреляции. = 0,05 оценить значимость коэффициента корреляции.Нулевая гипотеза 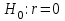 ; конкурирующая гипотеза ; конкурирующая гипотеза 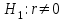 . .Наблюдаемое значение критерия: 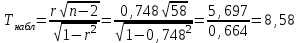 . .По уровню значимости 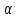 = 0,05 и числу степеней свободы = 0,05 и числу степеней свободы 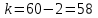 находим по таблице находим по таблице 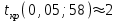 . .Поскольку 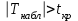 - нулевую гипотезу отвергаем. Другими словами, выборочный коэффициент корреляции значимо отличается от нуля. - нулевую гипотезу отвергаем. Другими словами, выборочный коэффициент корреляции значимо отличается от нуля.в) используя соответствующее уравнение регрессии, оценить стоимость квартиры общей площадью 75 м2. Подставим в уравнение регрессии 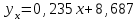 ; ; 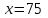 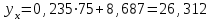 тыс. у. е. – стоимость квартиры. тыс. у. е. – стоимость квартиры. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||