Лабораторная работа 1. Решение б Решение в Решение г Решение
 Скачать 93.61 Kb. Скачать 93.61 Kb.
|
|
Задание 1 (Ким I, стр.83-87) 1. Даны звенья, которые описываются уравнениями: 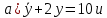 Решение: 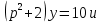 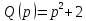 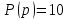 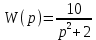 б) 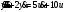 ; ; 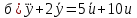 Решение: 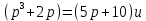 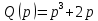 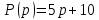 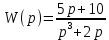 в) 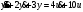 ; ; 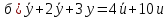 Решение: 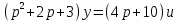 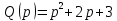 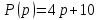 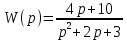 г) 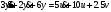 ; ; 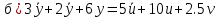 Решение: 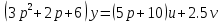 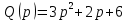 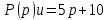 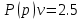 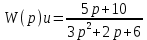 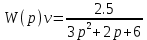 д) 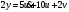 . .Решение: 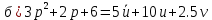 Здесь 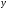 — выходная переменная, — выходная переменная, 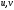 — входные переменные. Для каждого звена определить: — входные переменные. Для каждого звена определить:а) постоянные времени и передаточные коэффициенты; б) собственные операторы и операторы воздействия; в) передаточные функции. 2. Записать дифференциальные уравнения звеньев, заданных передаточными функциями: а) 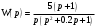 ; ; б) 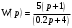 ; ; в) 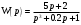 ; ; 3. Определить переходную и весовую функции следующих звеньев: a) 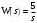 ; ; б) 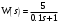 ; ; в) 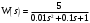 ; ; г) 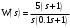 ; ; д) 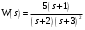 ; ; е) 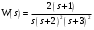 ; ;4. Определить реакцию в установившемся режиме на входное воздействие 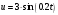 для следующих звеньев: для следующих звеньев:а) 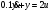 ; ; б) 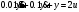 ; ; в) 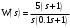 г) 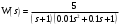 ; ;5. Построить амплитудно-фазовую частотную характеристику для следующих звеньев: а) 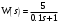 ; ; б) 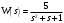 ; ; в) 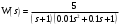 ; ; г) 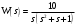 ; ;6. Выяснить, последовательным соединением каких элементарных звеньев можно представить следующие системы: а) 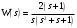 ; ; б)  ; ; в)  ; ; г)  ; ;7. Определить значения фазовой частотной функции при частотах  и и 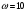 для следующих звеньев: для следующих звеньев: а) 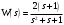 ; б) ; б) 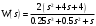 ; в) ; в) 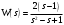 ; г) ; г)  ; ;8. Определить передаточные функции следующих систем:     . .8. Определить передаточные функции 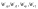 . .10. Для структурных схем, приведенных в задаче 9, нарисуйте граф системы управления и по теореме Мейсона определите передаточные функции 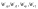 . .11. Построить асимптотические ЛАЧХ: а) ш(в) = М0(« + 1) • ; { } (0,1 82 + s) (0,0001 s2 + 0,01 s + 1)' , ( . = 10(0,01 s2 + 0,1 а + 1) . ; К ' (58 + 1)(0,25 s3 + 0,5 s2 + s)' 5(0,ls2 + b + 10) ; W (s + 5)(0,25s3 + 0,5s2 + s)' 12. Записать дифференциальное уравнение, связывающее выход ную переменную у с внешними воздействиями д и / для системы Wi = 0,lp + 0,2±, W2 = ^, ^з = 0,4, ^4 = 0,5. р р(0,5р+1) Для системы, представленной в предыдущем пункте, записать дифференциальное уравнение, связывающее ошибку е с внешними воздействиями д и /. По асимптотическим ЛАЧХ звеньев записать их передаточные функции, не имеющие нулей и полюсов в правой полуплоскости: |
