Задача. Решение. Ч ерез прямую lt проводим вспомогательную горизонтальнопроецирующую плоскость . L t , x
 Скачать 23.94 Kb. Скачать 23.94 Kb.
|
|
Задача 7 Построить точку пересечения прямой LT с заданной плоскостью. Показать видимость прямой относительно заданной плоскости. Дано: общего положения прямая LT и плоскость , заданную прямоугольником АВСD. Решение. 1.Через прямую LT проводим вспомогательную горизонтально-проецирующую плоскость . 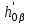 L=T, L=T, 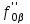 x. x.2. Строим линию пересечения EF заданной и вспомогательной плоскостей: E = AB 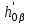 ; ;E находится в пересечении линии проекционной связи, проведенной из Е, и AB; F = DC 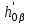 ; ;F находится в пересечении линии проекционной связи, проведенной из F, и DC. 3. Строим точку пересечения K заданной прямой LT и линии пересечения EF: K = LT EF АВС''D”; По линиям связи находим точку пересечения К'/ 4. Определяем взаимную видимость прямой LT и прямоугольника АВСD с помощью конкурирующих точек На горизонтальной плоскости проекций выбираем конкурирующие точки в пересечении LT с любой из проекций прямых, принадлежащих плоскости прямоугольника АВСD, например 1 Е = = LT AB: 1 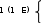 LT; LT;E AB. В направлении на плоскость 1 точка E «закрывает» точку 1, следовательно, на горизонтальной плоскости проекций отрезок 1K невидим. На фронтальной плоскости проекций выбираем конкурирующие точки в пересечении LT с любой из проекций прямых, принадлежащих плоскости прямоугольника АВСD, например 2 3 = LT AC: 3 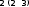 LT; LT; 2 AC. В направлении на плоскость 2 точка 3 «закрывает» точку 2, следовательно, на фронтальной плоскости проекций отрезок 3K видимый. |
