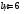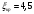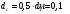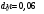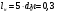Задача гидравлика. Решение Число Рейнольдса при истечении жидкости из отверстия определяют по формуле (1) следовательно, трубопровод работает в квадратичной зоне
 Скачать 127.99 Kb. Скачать 127.99 Kb.
|
|
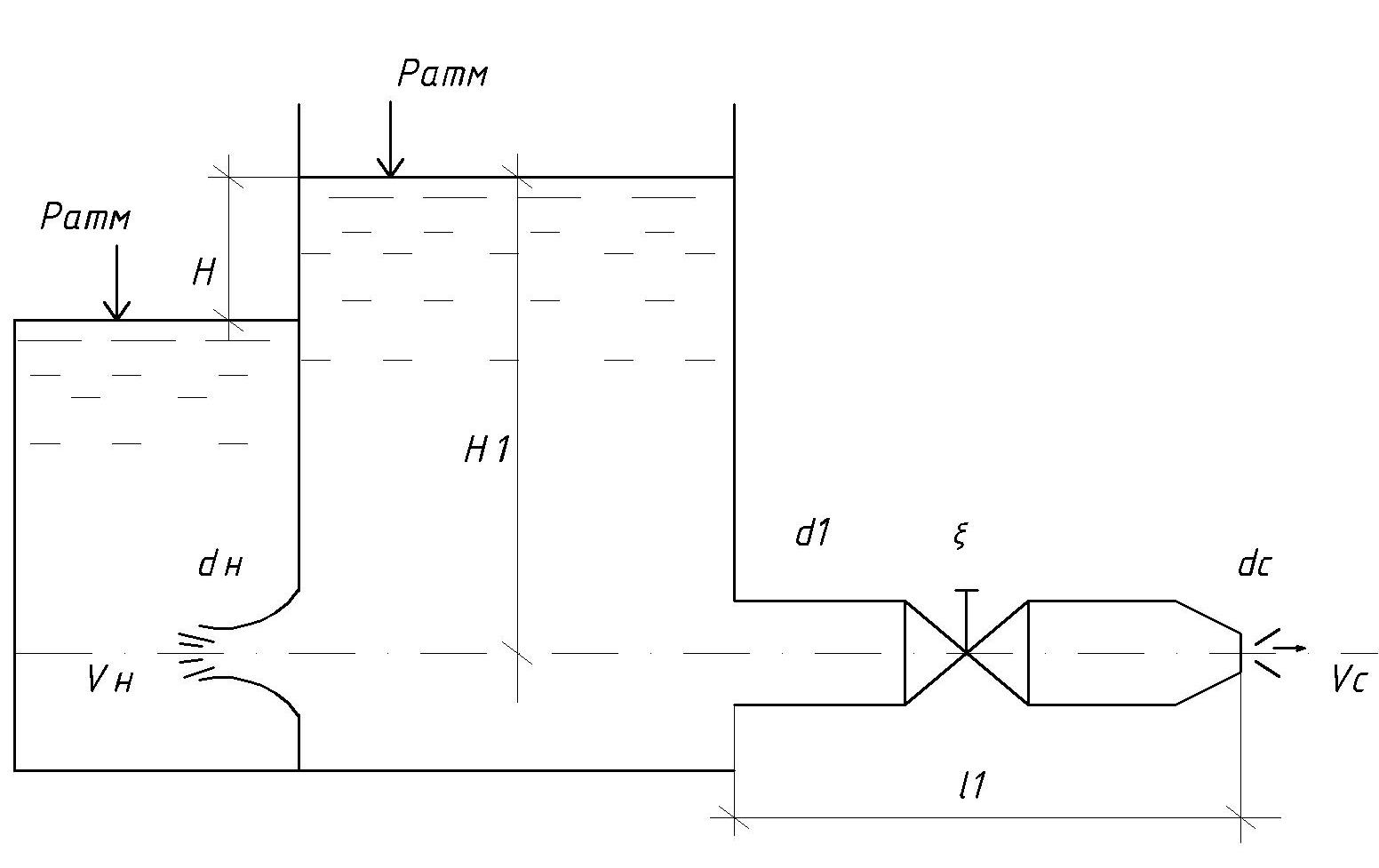
Задача 15 Из открытого резервуара по короткому стальному трубопроводу постоянного поперечного сечения d1 и длиной l1 с краном, коэффициент сопротивления которого ζкр, заканчивающимся соплом диаметром dс = 0,5d1, вытекает вода в атмосферу. Истечение происходит под напором Н1. С другой стороны к резервуару присоединен коноидальный насадок диаметром выходного сопла dн и длиной lн = 5 dн, истечение из которого происходит при разности уровней в резервуарах Н. Определить: Скорость истечения из сопла vc и расход воды по короткому трубопроводу Qc. Расход воды через затопленный коноидальный насадок Qн. Дано:
Решение: 1.Число Рейнольдса при истечении жидкости из отверстия определяют по формуле: 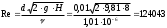 (1) (1)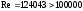 следовательно, трубопровод работает в квадратичной зоне. следовательно, трубопровод работает в квадратичной зоне.2. При расчете коротких трубопроводов следует учитывать не только местные потери напора, но и потери на трение. Расход жидкости из трубопровода (истечение в атмосферу) постоянного диаметра d и длиной l, работающего под напором Н, определяют по формуле: 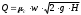 (2) (2)3. Для определения коэффициента расхода системы, необходимо найти коэффициент гидравлического трения и учесть местные сопротивления (сопло рассчитать, а сопротивление крана дано по заданию): Коэффициент сжатия равен: 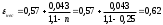 (3) (3)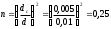 (4) (4)Коэффициент местного сопротивления при внезапном сужении: 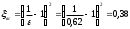 (5) (5)Коэффициент гидравлического трения: 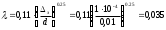 (6) (6)Коэффициент расхода системы: 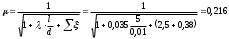 (7) (7)По формуле (2) определим расход: 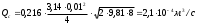 4. Скорость вытекания жидкости из отверстия определяют по формуле: 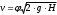 (8) (8)Коэффициент скорости, учитывает потери напора, обусловленные протеканием жидкости через отверстие: 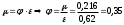 (9) (9)Определим скорость истечения: 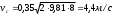 5. Расход через затопленный насадок определяется по формуле: 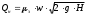 (10) (10)Так как, размеры отверстие малы по сравнению с размерами емкости 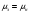 , коэффициентом расхода насадки μн=0,97 , коэффициентом расхода насадки μн=0,97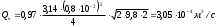 Ответ: 1. 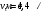 , , 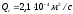 ; ;2. 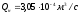 |