теория вероятности. Решение Чтобы число делилось на 5, на конце должен стоять 0 или 5

• Название: Решение Чтобы число делилось на 5, на конце должен стоять 0 или 5
• Анкор: теория вероятности
• Дата: 16.10.2022
• Размер: 133.49 Kb.
• Имя файла: 35563.docx
• Тип: Решение; #736719

1. Для доступа в компьютерную сеть оператору необходимо набрать пароль из 6 цифр. Оператор забыл или не знает необходимого кода. Сколько всевозможных комбинаций он может составить для набора пароля, если число-пароль нацело делится на пять и все цифры различны (предполагается, что цифра 0 может стоять на первом месте).

Решение:

Чтобы число делилось на 5, на конце должен стоять 0 или 5.

Пусть на конце стоит 0, тогда оставшиеся 5 цифр мы можем расположить числом размещений из 9 цифр по 5: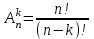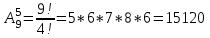





Пусть на конце стоит 5, тогда оставшиеся 5 цифр мы можем расположить числом размещений из 9 цифр по 5: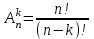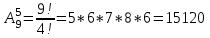





Искомое число способов равно сумме вычисленных размещений:

N=15120+15120=30240

Ответ: N=30240 способов
2. Подбрасываются три игральные кости. Найти вероятность того, что числа очков на трех костях совпадут.

Решение:

событие А – числа очков на трех костях совпадут.

используем классическое определение вероятности: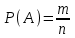



m – число благоприятных исходов,

n-число элементарных исходов.

Число элементарных исходов равно 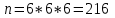(на каждой кости может выпасть любое из 6 чисел)

число благоприятных исходов равно: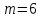

(то есть на костях могут выпасть одни 1 или одни 2, или одни 3, или один 4, или одни 5, или одни 6)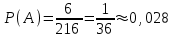



Ответ: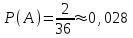
3. Из 2 первокурсников, 6 второкурсников и 5 третьекурсников выбирают 4 человека на конференцию. Найти вероятность того, что все первокурсники попадут на конференцию.

Решение:

событие А - все первокурсники попадут на конференцию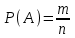



m – число благоприятных исходов,

n-число элементарных исходов.

Число различных способов выбора 4 человек из 2+6+5=13 равно числу сочетаний из 13 по 4: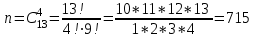



выбрать 2 первокурсников можно числом перестановок: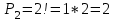



выбрать оставшихся 2 человек числом сочетаний из 6+5=11 по 2: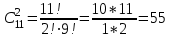



Тогда число благоприятных исходов равно произведению:

m=2*55=110

Тогда: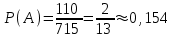



Ответ: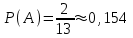
4. Вероятность того, что колбаса высшего сорта равна 0,9. Найти вероятность того, что из четырех проверенных сортов колбасы только три высшего сорта.

Решение:

события

А – из четырех проверенных сортов колбасы только три высшего сорта

используем формулу Бернулли: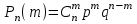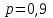

,



q=1-р=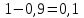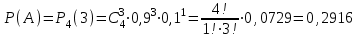



Ответ: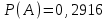
5. Из цифр {1, 2, 3, 4, 5} сначала выбирается одна, а затем вторая цифра (наудачу). Какова вероятность, что полученное двузначное число является четным?

Решение:

рассмотрим событие А – полученное двузначное число является четным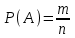



m – число благоприятных исходов,

n-число элементарных исходов.

Найдем число элементарных исходов:

первую цифру можем выбрать как любую из 5 данных цифр, вторую цифру можем выбрать как любую из оставшихся 4 цифр, тогда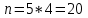



Найдем число элементарных исходов:

число будет четным, если на конце стоит 0 или 2, или 4.

Значит цифру на втором месте мы можем выбрать из цифр 0,2,4, а первую цифру можем выбрать как любую из оставшихся 4, тогда

m=3*4=12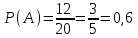



Ответ: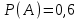
6. Вероятность хотя бы одного попадания в цель при трёх выстрелах равна 0,784. Найти вероятность попадания при одном выстреле.

Решение:

Вероятность хотя бы одного попадания находим по формуле: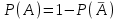

,

где событие 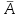- нет ни одного попадания при трех выстрелах



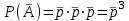р- вероятность попадания при одном выстреле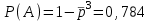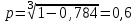





Ответ: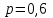
7. Вероятность того, что клиент не выплатит банку кредит, равна 0,3. Найти вероятность того, что из 100 клиентов банка кредит выплатят более 95 человек.

Решение:

используем интегральную формула Муавра Лапласа: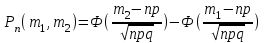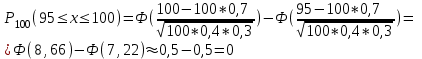

,


Ответ: Р=0
8. Дискретная случайная величина 𝜉 задана рядом распределения:

𝜉	-10	10	20	50	60
𝑃	0,1	0,2	0,25	𝑝	0,15

Найти:

а) неизвестную вероятность 𝑝;

б) функцию распределения 𝐹(𝑥) и построить её график;

в) математическое ожидание𝑀[𝜉];

г) дисперсию 𝐷 𝜉;

д) 𝑃 ^(-10 ≤ 𝜉 ≤50).

Решение:

а) неизвестную вероятность найдем исходя из того, что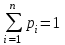

0,1+0,2+0,25+р+0,15=1

р=0,3

б) Функция распределения: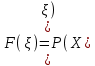



Если 𝜉 ≤-10, то F(𝜉)=0,

-10< 𝜉 ≤10, то F(𝜉)=0,1,

10< 𝜉 ≤20, то F(𝜉)=0,1+0,2=0,3,

20
50< 𝜉 ≤60, то F(𝜉)=0,55+0,3=0,85,

𝜉 >60, то F(𝜉)=0,85+0,15=1.



Рис.1. График функции распределения
в) математическое ожидание: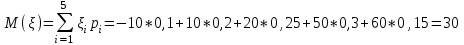



г) Дисперсия: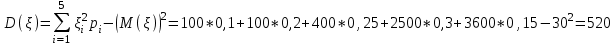



д) 𝑃 ^(-10 ≤ 𝜉 ≤ 50)=Р(-10)+Р(13)+Р(20)+P(50)=0,1+0,2+0,25+0,3=0,85
9 Игральную кость подбрасывают три раза. Случайная величина 𝜉 – число выпадений «шести» очков. Построить вероятностный ряд для𝜉. Найти ее 𝑀[ξ] и 𝐷[ξ].

Решение:

Возможные варианты 𝜉: 0,1,2,3

используем формулу Бернулли: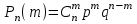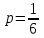

,



q=1-р=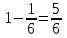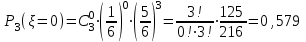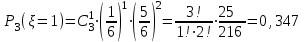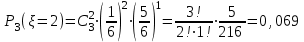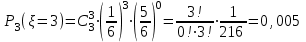








получили вероятностный ряд

𝜉	0	1	2	3
р	0,579	0,347	0,069	0,005

математическое ожидание: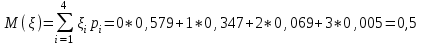



Дисперсия: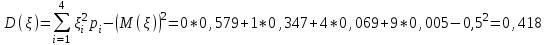


10. Непрерывная случайная величина 𝜉 задана с помощью функции -плотности распределения вероятностей𝑓(𝑥):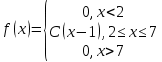



Найти: а) параметр 𝐶;

б) функцию распределения 𝐹 𝑥 и построить ее график;

в) математическое ожидание𝑀 𝜉 и дисперсию 𝐷[𝜉];

г) 𝑃 ⁽³ ≤ 𝜉<10).

Решение:

а) Коэффициент С найдем из условия: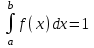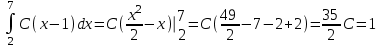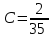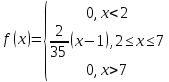







б)

Найдем функцию распределения

1)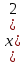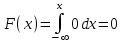



2)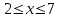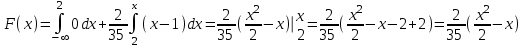

  

3)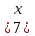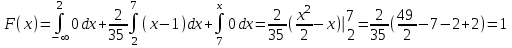

 

Функция распределения имеет вид: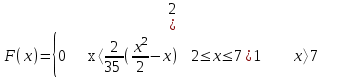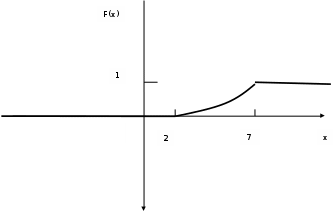




в)

Математическое ожидание: =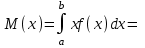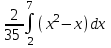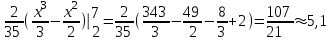

=

Дисперсия: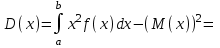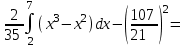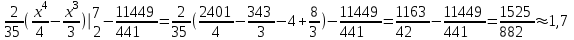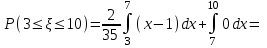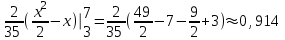

=


11. Случайная величина 𝜉 распределена равномерно на [0; 10]. Написать𝑓(𝑥)и 𝐹(𝑥). Найти 𝑀[𝜉] и 𝐷[𝜉]. Вычислить 𝑃 (2 ≤ 𝜉 ≤ 15).

Решение:

определению плотность равномерно распределенной на отрезке [a,b] случайной величины Х имеет вид: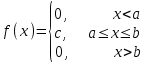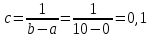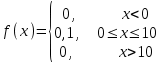

,





функция распределения F(x) равномерно распределенной отрезке [a,b] случайной величины Х :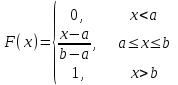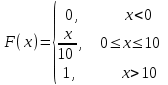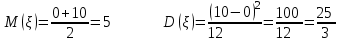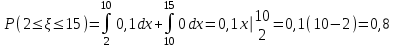

.








12. Случайная величина 𝜉 распределена нормально с математическим ожиданием 𝑀[𝜉] = 7 и дисперсией 𝐷 𝜉 = 16. Написать ее функцию плотности распределения вероятностей 𝑓(𝑥) и вычислить 𝑃 (3≤𝜉≤11).

Решение: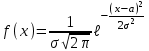



а= 𝑀[𝜉] =7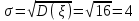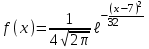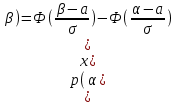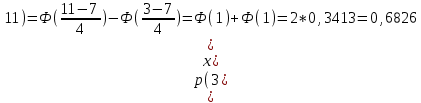