эл тех. ргр1. Решение данной задачи рассматривается при следующих исходных данных s ном
 Скачать 123.38 Kb. Скачать 123.38 Kb.
|
|
Решение данной задачи рассматривается при следующих исходных данных: Sном = 100 кВ∙А; U1ном = 35 кВ; U2ном = 660В; Pх = 0.9 кВт; Pк = 3 кВт; Uк = 9%; φ2 = -10⁰; группа соединения обмоток Y/ 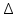 – 11. Это решение осуществляется в следующем порядке. – 11. Это решение осуществляется в следующем порядке. Составляется схема электрической цепи нагруженного трансформатора (рис 33). 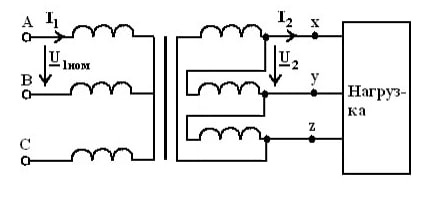 Определяется коэффициент трансформации. Так как обе обмотки соединены звездой, то линейный nл и фазный nф коэффициенты трансформации равны: nл =U1ном/ U2ном=35000/660=53 Определяются фазные номинальные напряжения первичной и вторичной обмоток: U1Ф ном= U1ном/ 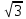 =35000/1.73=20231B; =35000/1.73=20231B; U2Ф ном= U2ном =660В (т.к. соединение треугольником) nф= U1ф/ U2ф=20231/660=30.653 Определяются значения номинальной мощности и мощностей потерь при опытах холостого хода и короткого замыкания, приходящиеся на одну фазу: SФ ном= Sном/ 3=10/3=33кВ*А; PХФ=РХ/3=0.9/3=0,3 кВт; PКФ=РК/3=3/3=1 кВт; Определяются номинальные токи первичной и вторичной обмоток. Так как обмотки соединены звездой, то линейный и фазный токи равны: I1 ном= I1Ф ном= SФ ном/ U1Ф ном=33000/20231=1.6A;(т.к. соединение звездой) I2 ном= I2Ф ном* 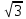 =50*1.73=86.5А =50*1.73=86.5АI2Ф ном= SФ ном/ U2Ф ном=33000/660=50A; Определяются внешняя характеристика трансформатора, представляющая зависимость вторичного напряжения U2 от тока нагрузки I2 или от величины β, которая пропорциональна току нагрузки (β = I2 / I2ном). Зависимость U2(β) определяется в следующем порядке. Определяются активная Uак и реактивная Uрк составляющие напряжения короткого замыкания в процентах от U1Ф ном: Uак= 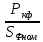 *100= *100=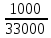 *100=3.03 *100=3.03Uрк= 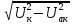 = =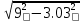 =8,5 =8,5Определяется зависимость относительного изменения вторичного напряжения 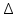 U2от коэффициента нагрузки β по формуле U2от коэффициента нагрузки β по формуле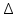 U2= β(Uакcosφ2+ Uрк sinφ2). При β = 0,6 и φ2 =-10⁰ получаем: U2= β(Uакcosφ2+ Uрк sinφ2). При β = 0,6 и φ2 =-10⁰ получаем: 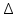 U2 =0,6(3.03*0.98+8.5*(-0.17))=0,915. Значения U2 =0,6(3.03*0.98+8.5*(-0.17))=0,915. Значения 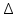 U2для остальных значений βприведены в табл. 20. U2для остальных значений βприведены в табл. 20.Определяется зависимость 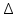 U2(β) по формуле U2(β) по формуле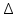 U2(β)= U2 ном*(1- U2(β)= U2 ном*(1- 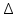 U2/100). При β =0,6 получаем U (β)=660(1-0,915/100). Значения U2(β) для остальных значений β приведены в табл. 20. U2/100). При β =0,6 получаем U (β)=660(1-0,915/100). Значения U2(β) для остальных значений β приведены в табл. 20.Определяется зависимость коэффициента полезного действия трансформатора от коэффициента нагрузки β по формуле: η(β)= 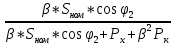 При β =0,6 получаем η(β)= 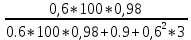 =0,967 =0,967Значения η(β) для остальных значений β приведены в табл. 20.
На основании данных табл. 20 строятся графики зависимостей U2 (β) и η ( β ) ЗАДАЧА 12. Расчет характеристик асинхронного трехфазного двигателя с короткозамкнутым ротором. Решение данной задачи рассматривается при следующих исходных данных: Pном = 75 кВт; nном = 2900 об/мин; ηном= 0,92; cosφном = 0,9; λ = Mmax / Mном = 2.2; Iп / Iном = 7; Uном = 220 В; p = 1; обмотка статора соединена в треугольник. Это решение осуществляется в следующем порядке. 1. Определяется номинальная мощность, потребляемая двигателем: Р1ном=Рном/ηном=75/0.92=86 2. Определяются номинальный и пусковой токи: Iном =Р1ном/( 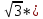 Uном* cosφном)=86000/(1.73*220*0,9)=251A; Uном* cosφном)=86000/(1.73*220*0,9)=251A;In=7* Iном=7*251=1757A. 3. Определяются частота вращения поля статора n1, номинальное Sном и критическое Sкр скольжения: n1 =60f/p=60*50/1=3000 об/мин; Sном=(n1-nном)/n1=(3000-2900)/3000=0.033 или 3.3%; Sкр= Sном( 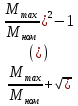 =0.033(2.2+ =0.033(2.2+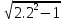 )=0.14 или 14% )=0.14 или 14%4. Определяются номинальный и максимальный моменты на валу двигателя: Mном=9550Рном/nном=9550*75/2900=247 Н*м; Мmax=1.8Мном=1.8*247=445 Н*м; Зависимость момента от скольжения M(S) и механическая характеристика n(M) рассчитываются в следующем порядке. Для заданного ряда значений S (он приведен в табл. 23) определяются значения частоты вращения ротора n и момента на валу M по формулам: n=n(1-S): M= 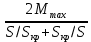 ; ;При S = 0,2 получаем: n = 3000(1 – 0,2) = 2400 об / мин; M= 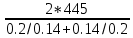 =418 =418Значения n и M для остальных значений S приведены в табл. 23.
Первая графа этой таблицы соответствует холостому ходу двигателя, при котором момент на валу MХ = 0, скольжение SХ ≈ 0, частота вращения ротора nХ = n1 = 3000 об / мин. Вторая и третья графы соответствуют номинальному и критическому скольжениям Последняя графа соответствует началу пуска двигателя. Из нее следует, что пусковой момент двигателя MП = 122 Н∙м. По данным табл. 23 строятся графики зависимостей M(S) и n(M). 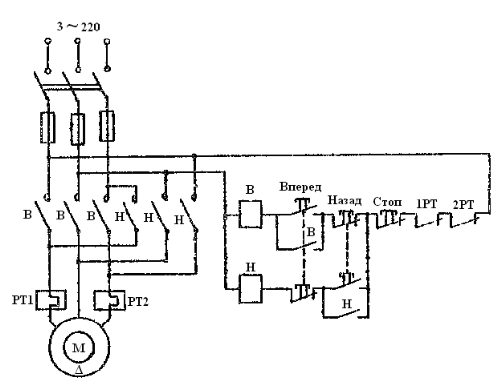 ЗАДАЧА 14. Расчет характеристик двигателя постоянного тока параллельного возбуждения Решение данной задачи рассматривается при следующих исходных данных Uном=220В;. Рном=6 кВт; nном=1500 об / мин; ηном= 0,82;RЯ=0,62Ом;RB=220 Ом;МП/Мном=2,4. Это решение осуществляется следующим образом. Определяются величины, относящиеся к естественной характеристике двигателя при номинальном режиме работы, а именно: номинальная мощность, потребляемая двигателем от сети Р1ном=Рном/ηном=6/0,82=7,3кВт; номинальный ток двигателя Iном =Р1ном/Uном=7300/220=33А; номинальный ток возбуждения IВ ном =Uном/RB=220/220=1А; номинальный ток якоря IЯ ном=Iном-IВ ном=33-1=32А; номинальное напряжение ЭДС Eном= Uном- RЯ* IЯ ном=220-0.62*32=200В; номинальный момент на валу Мном=9550 Рном/ nном=38,2Н*м Определяются числовые значения величин CeФном, СмФном и СеСмФном2, которые широко используются как вспомогательные величины при дальнейшем решении задачи. Величина CeФном определяется из уравнения номинальной ЭДС:Eном=Cе*Фном*nном, из которого получаем: CeФном= Eном/ nном=200/1500=0,133. Величина СмФном определяется из уравнения номинального момента , из которого получаем: Мном= СмФном IЯ ном, из которого получаем: СмФном= Мном/ IЯ ном=38,2/32=1,2. Величина СеСмФ2ном=0.133*1,2=0.1596 Так как характеристики n(M), n(M)1, n(M)2 получаются при одном и том же потоке возбуждения Фном, то частоты вращения якоря при холостом ходе двигателя nx, nx1, nx2, относящиеся к этим характеристикам, оказываются равными. Частота вращения nx определяется из уравнения естественной механической характеристики при холостом ходе двигателя: nx= Uном/ CeФном=220/0,133=1654 об / мин. График естественной механической характеристики n(M) проходит через точку nx и точку с координатами Mном, nном .(рис 44) График первой реостатной механической характеристики n(M)1 проходит через точку nx и точку MП, так как пуск двигателя начинается согласно этой характеристике: MП=2 Mном=2.4*38,2=91.68Н*м. По этому графику определяется частота вращения якоря nном1, которую будет иметь двигатель, работая согласно данной характеристике с моментом на валу, равным номинальному. Получилось nном1= График второй реостатной механической характеристики n(M)2 проходит через точку nx и по условию задачи занимает среднее положение между характеристиками n(M) и n(M)1. При этом условии частота вращения nном2, которую будет иметь двигатель, работая согласно характеристике n(M)2 с моментом на валу, равным номинальному, определяется как среднее арифметическое от nном и nном1: nном2=( nном+nном1)/2= График первой полюсной механической характеристики n(M)3 проходит через точку nх3 и точку с координатами Mном; nном3. Частота вращения якоря nx3, которую будет иметь двигатель, работая на холостом ходу согласно данной характеристике, определяется по формуле nx3= Uном/(0.75 CeФном)=220/(0,75*0,133)=2206 об / мин Частота вращения якоря nном3, которую будет иметь двигатель, работая согласно данной характеристике с моментом на валу, равным номинальному, определяется из уравнения данной механической характеристики nном3= 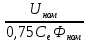 - Мном - Мном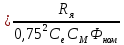 = =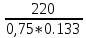 -38,2* -38,2*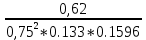 =222 об/мин =222 об/минГрафик второй полюсной механической характеристики n(M)4 проходит через точку nX4и точку с координатами Мном; nном4. Частота вращения якоря nX4, которую имеет двигатель, работая на холостом ходу согласно данной характеристике определяется по формуле nX4= Uном//(0.5 CeФном)=220/(0.5*0.133)=3308 об / мин. Частота вращения якоря nном4 , которую будет иметь двигатель, работающий согласно этой характеристике с моментом на валу, равным номинальному, определяется из уравнения данной механической характеристики: nном4= 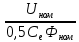 - Мном - Мном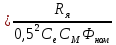 = =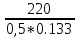 -38,2* -38,2*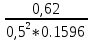 =2715 об/мин =2715 об/минГрафики механических характеристик, построенные согласно полученным данным, приведены на рисунке 44. Сопротивление пускового резистора RП2 определяется из уравнения второй реостатной механической характеристики двигателя при моменте на валу, равном номинальному: nном2= 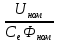 - Мном - Мном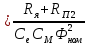 ; ;Сопротивление пускового реостата RП1 определяется из уравнения первой реостатной механической характеристики двигателя при моменте на валу, равном номинальному: nном1= 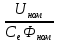 - Мном - Мном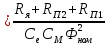 ; ;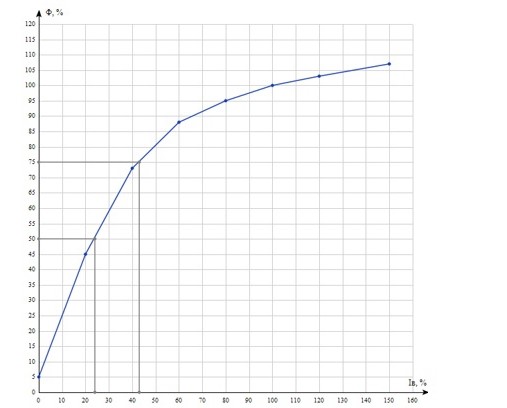 По данным таблице 31 строится вебер-амперная характеристика двигателя (рисунок 45) и посредством ее определяются значения токов возбуждения IВ3 и IВ4 в процентах от IВ.НОМ при работе двигателя согласно характеристикам n(M)3 и n(M)4. Они получились равными 44 и 22 % соответственно. Значения этих токов в амперах равны: IВ3=0,44А и IВ4=0.22 А Сопротивление резистора RП1 определяется из уравнения электрического состояния цепи возбуждения, относящегося к первой полюсной характеристике: Uном= IВ3( 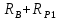 ) , из которого получается: ) , из которого получается: 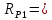 Uном/ IВ3- Uном/ IВ3-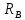 =220/0,44-220=280Ом. =220/0,44-220=280Ом.Сопротивление резистора RР2 определяется из уравнения электрического состояния , относящегося ко второй полюсной характеристике: : Uном= IВ4( 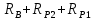 ), из которого получается: ), из которого получается: 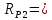 Uном/ IВ4- Uном/ IВ4-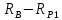 =220/0.22-220-280=500Ом =220/0.22-220-280=500Ом |
