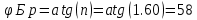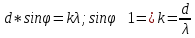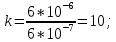физическая оптика. Азимбаев В.Т ОКз-21. Решение Дано 50 о 35 о Найти n Ответ n 34
 Скачать 0.51 Mb.
|
|
Задача 1 Определить показатель преломления жидкости, если известно, что при угле падения 50о угол преломления 35о . Решение: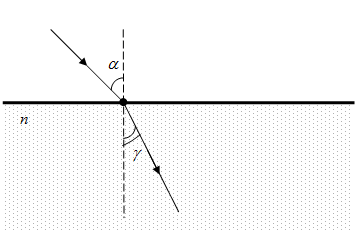 
Задача 2 Определите на какой угол отклоняется световой луч от своего первоначального направления при переходе из воздуха в воду, если угол падения 80о (показатель преломления воды 1,33). Решение:
Задача 3 Определить угол Брюстера для стекла с показателем преломления 1,60. Решение: При угле падения, равном углу Брюстера φБр: 1. отраженный от границы раздела двух диэлектриков луч будет полностью поляризован в плоскости, перпендикулярной плоскости падения; 2. степень поляризации преломленного луча достигает максимального значения меньшего единицы; 3. преломленный луч будет поляризован частично в плоскости падения; 4. угол между отраженным и преломленным лучами будет равен 90°; 4. тангенс угла Брюстера равен относительному показателю преломления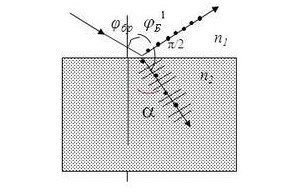 
Задача 4 На дифракционную решетку нормально к её поверхности падает параллельный пучок лучей с длиной волны 0,6 мкм. Период дифракционной решетки составляет 6 мкм. Определите, сколько максимумов дает дифракционная решетка и максимальный угол отклонения лучей, соответствующих последнему дифракционному максимуму. Решение: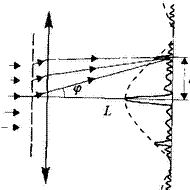 
Конспект Оптический диапазон длин волн: Оптические волны – разновидность электромагнитных волн (от радио волн до гамма лучей) в узком диапазоне, различают оптические волны видимого диапазона в интервале 400 нм<<700 нм, инфракрасное излучение в интервале 700 нм<<1мм и ультрафиолетовое излучение в интервале 1 нм<<400нм. Поляризация света: Н 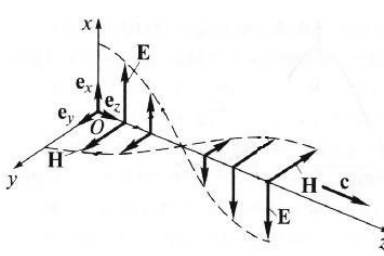 а рисунке изображена ситуация, когда вектор Е колеблется вдоль оси Ox, а вектор Н – вдоль Oy. В этом случае говорят, что волна плоскополяризованна. Плоскость поляризации – это плоскость, в которой колеблется вектор Е (в данном случае плоскость Oxz).Возможна и другая ситуация, когда вектор Е колеблется вдоль оси Оy, а вектор Н – вдоль оси Оx, при этом Е, Н и е также должны образовывать правую тройку векторов. Суперпозиция обеих ситуаций приводит к электромагнитной волне, у которой векторы Е и Н, оставаясь взаимно перпендикулярными, могут менять направление в плоскости Оxy. В этом случае волна будет эллиптически поляризованной. Действительно, пусть в некоторой плоскости z=const электрическое поле представляет собой суперпозицию гармонических полей, колеблющихся с одинаковой частотой вдоль осей Оx и Оy 𝐄(t) = 𝐞𝐱Ax cos(kz − t + 1 ) + 𝐞𝐲Ay cos(kz − t + 2 ), где ex и ey – единичные векторы. Конец вектора Е будет, в общем случае, двигаться по эллиптической траектории. Направление движения конца вектора Е вдоль траектории и ориентация эллипса относительно осей Оx и Оy зависят от разности фаз Δ = 2 − 1Все траектории в пространстве заключены в прямоугольнике 2Ax2Ay. При Δ = 0, поляризация называется линейной. При Δ = ⁄2 , 3⁄2 и Ax = Ay поляризация называется круговой. Принято определять направление вращения конца вектора E с точки зрения наблюдателя, который смотрит навстречу волне. При движении конца вектора E по часовой стрелке поляризация называется правой, а при движении против часовой – левой. 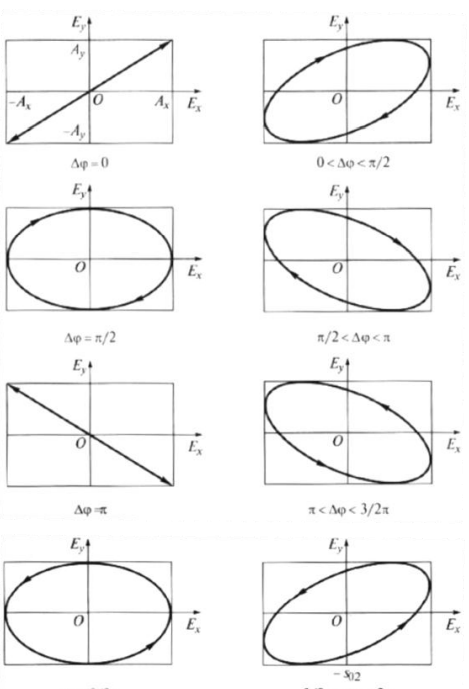 Законы отражения и преломления, угол Брюстера и полное внутреннее отражение: При падении светового луча на границу двух сред происходит преломление и отражение луча. П 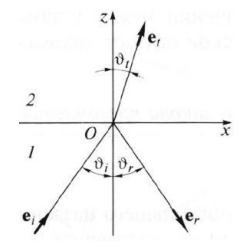 адающий луч, лежащий в плоскости падения Oxz, составляет угол i с нормалью к границе раздела. Его направление задается единичным вектором 𝐞𝐢. Отраженный луч ориентирован в направлении единичного вектора 𝐞𝐫, составляющего угол r с нормалью, а преломленный – в направлении 𝐞𝐭 под углом t к нормали. Запишем напряженности электрического поля этих трех волн 𝐄𝐢,𝐫,𝐭 = 𝐀𝐢,𝐫,𝐭 cos (→𝐤 →𝐫 −t + φ0). Аргумент функции можно расписать следующим образом 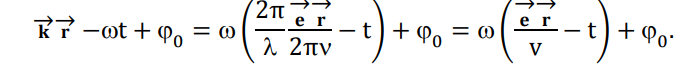 Здесь v = = c⁄n – фазовая скорость волны. Поле в первой среде есть сумма полей падающей и отраженной волн, а во второй среде определяется полем лишь одной преломленной волны 𝐄𝟏 = 𝐄𝐢 + 𝐄𝐫, 𝐄𝟐 = 𝐄𝐭. Граничные условия требуют непрерывности тангенциальных (лежащих в плоскости Oxy) компонент E1 = E2. Непрерывность тангенциальных компонент будет выполняться, если аргументы функций напряженности электрического поля изменяются синхронно, т.е. одинаковы в любой момент времени 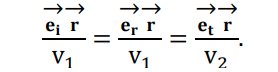 Так как вектор 𝐫⃗ лежит в плоскости Oxу, то это соотношение можно записать в следующем виде 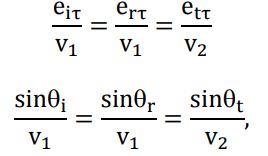 откуда следуют закон отражения i = r и закон преломления (закон Снеллиуса) sini/sint = v1/v2 = n2/n1. Есть материалы с отрицательным показателем преломления. При падении света в среду с n2 < 0 угол t < 0. Это означает, что преломленный луч будет находиться по одну сторону от нормали с падающим. В этом случае слой формирует изображение точечного источника. Важно отметить, что какой бы угол не образовывали падающие лучи с нормалью к поверхности материала, все прошедшие лучи пересекутся в одной точке. Поэтому такой слой называют суперлинзой. Однако в отличие от обычной линзы он не фокусирует коллимированный пучок света. Электрическое и магнитное поля можно представить в виде векторной суммы параллельной (лежащей в плоскости падения Oxz) и перпендикулярной компонент 𝐄 = 𝐄‖ + 𝐄┴, 𝐇 = 𝐇‖ + 𝐇┴. (2.10) Вначале положим, что электрическое поле 𝐄 = 𝐄‖, как изображено на рис. 2.3. Так как векторы Е, Н и е образуют правую тройку векторов, то 𝐇 = 𝐇┴. Условие непрерывности E1 = E2 в этом случае примет вид Ei‖ cos i + Er‖ cos r = Et‖ cos t. Второе условие H1 = H2 означает, что Hi┴ + Hr ┴ = Ht┴. Вектора электрического и магнитного полей в диэлектрической среде (1) связаны соотношением  Второе граничное условие запишем в виде n1Ei‖ + n1Er‖ = n2Et‖. Таким образом, имеем систему уравнений 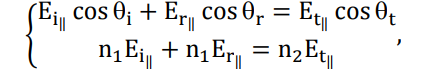 решая которую с использованием законов отражения и преломления можно получить следующие две формулы для поляризации, параллельной плоскости падения 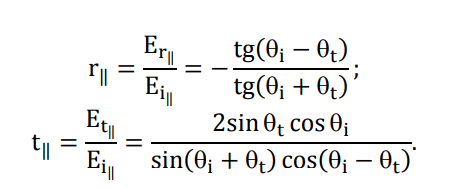 Рассуждая аналогично, можно получить формулы для поляризации, перпендикулярной плоскости падения 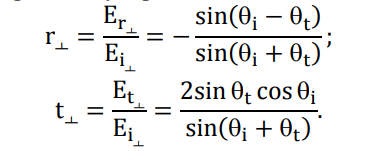 Поляризация, параллельная плоскости падения, называется p-поляризацией, а поляризация, перпендикулярная плоскости падения – s-поляризацией. Последние четыре формулы называются формулами Френеля, которые описывают коэффициенты отражения и пропускания для напряженности E электрического поля. На практике используют энергетические коэффициенты отражения R и пропускания T для интенсивности I = EH̅̅̅̅. При нормальном падении (i = 0) выражения для энергетических коэффициентов отражения и пропускания не зависят от поляризации света и записываются следующим образом 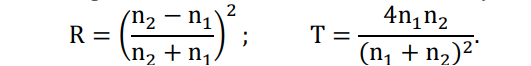 При распространении света из воздуха в стекло R=0,04, а T=0,96. Рассмотрим ситуацию, когда i + t = ⁄2. В этом случае r‖ = 0, т.е. одна из компонент не отражается. Соответствующий угол падения i = Б называется углом Брюстера. Применяя закон преломления, получим выражение для угла Брюстера sinБ/sint = sinБ/sin(π2−θБ) = tgθБ = n2/n1; θБ = arctg (n2/n1). Угол Брюстера для границы воздух-стекло равен 56°. При падении под углом Брюстера света, поляризованного в плоскости падения, его отражения не происходит. Этот эффект применяется в газовых лазерных генераторах, когда окна лазерной кюветы заклоняются на угол Брюстера. При многократном отражении от окон излучение с поляризацией, перпендикулярной плоскости падения, частично отражается, т.е. испытывает потери. Излучение с поляризацией, параллельной плоскости падения, не отражается, т.е. не испытывает потери и именно с этим излучением развивается генерация. Из закона преломления следует, что при падении света из оптически менее плотной в более плотную среду (n1 < n2) преломленный угол меньше падающего t < i . И наоборот, в случае падения света из оптически более плотной в менее плотную среду (n1 > n2) преломленный угол больше падающего t > i . При определенных условиях в последнем случае преломленный угол становится равным 90 и свет не проходит в оптически менее плотную среду. Такой угол падения называется углом полного внутреннего отражения. Величина этого угла находится из закона преломления 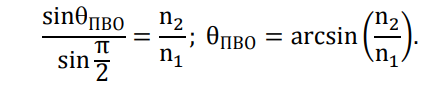 Угол полного внутреннего отражения для границы стекло-воздух равен 41o Интерференция света: Под интерференцией понимают явление наложения волн, приводящее к перераспределению в пространстве плотности энергии электромагнитного поля. Существует много схем для наблюдения интерференции, но во всех схемах реализуется наложение в пространстве световых волн.  Р 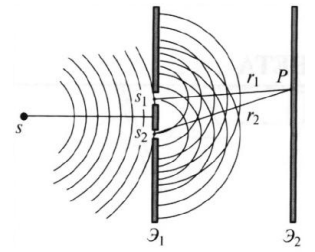 ассмотрим интерференционную схему Юнга. Свет от точечного источника s попадает на экран Э1 с двумя малыми близкорасположенными отверстиями, а на втором экране Э2 формируется интерференционная картина. Волновые возмущения в плоскости отверстий эквивалентны точечным источникам s1 и s2, посылающим в точку Р волны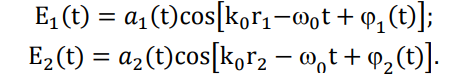 В общем случае амплитуды 1, 2 и фазы 1, 2 являются медленно меняющимися функциями времени. Можно показать, что интенсивность волны в точке Р равна  величина (r2 − r1) называется разностью хода. Это распределение интенсивности в пространстве описывает интерференционную картину, наблюдаемую на экране Э2. Интерференционные полосы Юнга: Проанализируем распределение интенсивности в интерференционной картине. Пусть 𝑎1 = 𝑎2 = 𝑎, 1 = 2 = const. В этом случае выражение для распределения интенсивности в интерференционной картине запишется в виде I = 2I0 [1 + cos(k0 (r2 − r1 ))]. 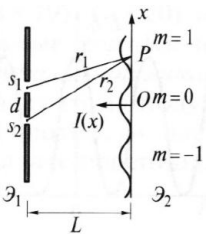 Здесь I0 = 𝑎2⁄2. В интерференционных максимумах интенсивность I = 4I0. Их положение определяется условием k0 (r2 − r1) = 2m или r2 − r1 = m0, где m = 0, 1; 2, … Целое число m определяет порядок интерференционного максимума или порядок интерференции. Если же k0 (r2 − r1) = 2m + или r2 − r1 = m0 + 0⁄2, то будут интерференционные минимумы, в которых I = 0. На экране Э2 будут видны практически параллельные полосы, называемые полосами Юнга. Они перпендикулярны плоскости рисунка.Дифракция света: Дифракция – это отступление от прямолинейного направления распространения света после прохождения препятствий. В переводе дифракция означает «разломанный». Законы дифракции объясняют распространение света во всех направлениях, заходя в область геометрической тени и огибая препятствия. Д 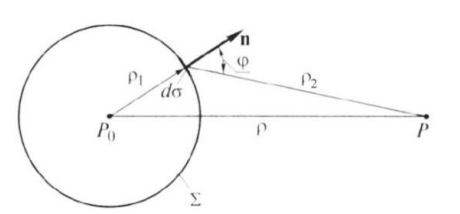 ля количественного описания дифракции Гюйгенс и Френель свели задачу о распространении волны к интерференции волн фиктивных вторичных источников следующим образом. Рассмотрим распространение сферической волны от точечного монохроматичного источника, расположенного в точке P0.В точке Р напряженность электрического поля будет равна 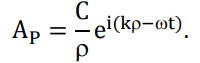 где С – константа, зависящая от мощности источника. Процесс распространения волны в точку Р можно представить также в два этапа. На первом этапе сферическая волна достигает некоторой произвольной сферической поверхности Σ, охватывающей источник. На этой поверхности как бы появляются вторичные источники. На втором этапе вторичные источники испускают свои сферические волны, которые интерферируют в точке Р. Однако, кроме частоты света, параметры этих источников неизвестны. Френель предположил, что возмущение, посылаемое элементарной площадкой, пропорционально ее площади d и зависит от угла наклона φ между нормалью к площадке и направлением в точку наблюдения. Так как в точке Р регистрируется интенсивность I = A̅2, в дальнейшем множитель e −it опускаем. В соответствии с двухэтапным рассмотрением можно получить выражение для напряженности электрического поля в точке P, которое называется дифракционным интегралом Гюйгенса-Френеля 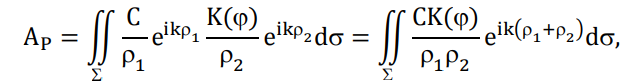 где K() = 1/(2) (1 + cos ) – коэффициент наклона. Зоны Френеля, зонная пластинка: Для вычисления дифракционного интеграла ГюйгенсаФренеля введем понятие зон Френеля. Для этого окружим точку P0 сферой радиусом 1 = α. Пусть точка Р расположена на расстоянии b от поверхности сферы. Мысленно циркулем, одна ножка которого находится в точке Р, проведем по поверхности сферы окружности. Соответствующие расстояния между ножками циркуля равны 2 = b + /2, b + 2/2, …, b + m/2. Тогда сфера будет разделена на кольцевые области, называемые зонами Френеля. Можно вывести формулы для радиуса и площади m-й зоны Френеля 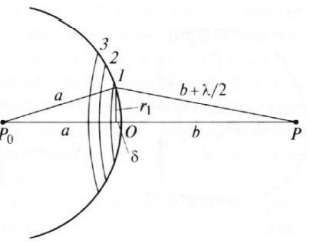 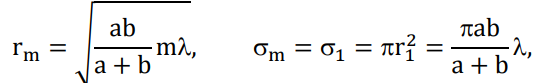 В общем случае формула, определяющая фазу для излучения, прошедшего через диафрагму радиусом R, записывается в виде R = σR/σ1, где R – площадь круга радиусом R, 1 – площадь первой зоны Френеля. Например, фаза для излучения, прошедшего через диафрагму радиусом R, которая соответствует N открытым зонам Френеля, равна RN = σRN/σ1 = Nσ1/σ1 = N. Здесь использовано то, что площади всех зон Френеля равны. |
; 
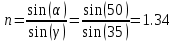
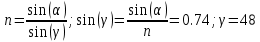
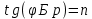