Электротехника. Решение. Политех. 19.. Решение Дано
 Скачать 382.25 Kb. Скачать 382.25 Kb.
|
|
Задача 2. В цепи постоянного тока заданы ЭДС 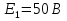 и сопротивления резисторов и сопротивления резисторов 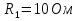 , , 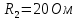 . Положения рубильников и остальные данные указаны в таблице 2. . Положения рубильников и остальные данные указаны в таблице 2.
Решение Дано: 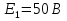 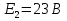 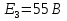 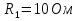 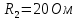 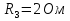
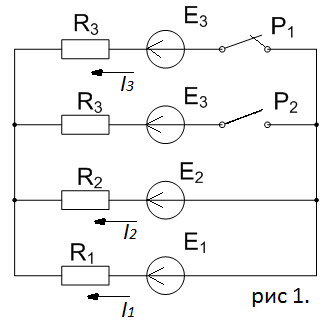 Заменим представленную расчетную схему - упрощенной эквивалентной ей. Нанесем на эквивалентную схему условные обозначения узлов и ветвей. 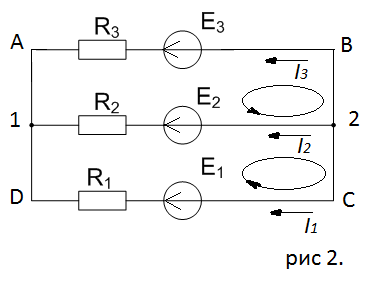
Для расчета электрической цепи постоянного тока по законам Кирхгофа необходимо составить в общем 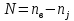 – число уравнений (1) – число уравнений (1)Где 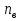 – общее число ветвей электрической цепи, – общее число ветвей электрической цепи,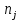 - число ветвей содержащих источники тока - число ветвей содержащих источники токаПо первому закону Кирхгофа максимальное число независимых уравнений равно: 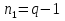 (2) (2)Где 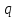 - число узлов электрической цепи - число узлов электрической цепиПо второму закону Кирхгофа максимальное число независимых уравнений равно: 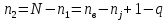 (3) (3)Из рис 2. Определяем: 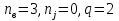 Таким образом, общее число уравнений по законам Кирхгофа равно: 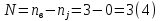 Число уравнений по первому закону Кирхгофа определяем из (2): 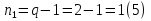 Число уравнений по второму закону Кирхгофа определяем из (3): 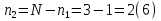 Таким образом, по первому закону Кирхгофа максимальное число независимых уравнений равно 1, по второму закону Кирхгофа максимальное число независимых уравнений равно 2. По первому закону Кирхгофа составим уравнение для узла 2 (рис 2.) 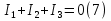 По второму закону Кирхгофа составим уравнения для контуров (A-B-2-1) и (C-D-1-2). Условные направления положительного обхода контуров показаны на (рис 2.). 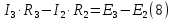 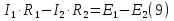 Уравнения (7),(8),(9) следует объединить в систему: 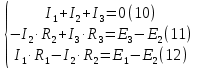 Подставляя, в полученную систему числовые значения получим: 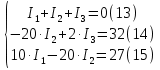
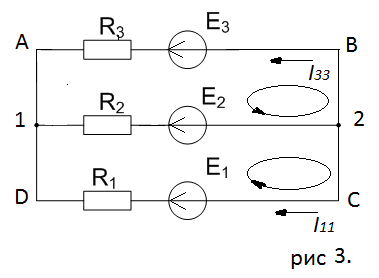 Для контуров (C-D-1-2), (A-B-2-1) составляем уравнения по второму закону Кирхгофа. 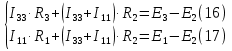 Подставляя, в систему числовые значения получим: 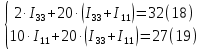 Решая, эту систему получим: 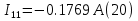 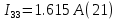 Теперь определим токи ветвей 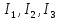 : :Из рис 2. и рис 3. видно что: 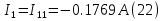 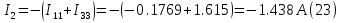 Знак минус указывает на то, что истинное направление тока 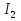 противоположно показанному на рис 2. противоположно показанному на рис 2.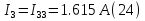
Принимаем потенциал узла (1) равным нулю т.е. 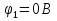 , а для узла (2) составляем уравнение по первому закону Кирхгофа (рис 2.). , а для узла (2) составляем уравнение по первому закону Кирхгофа (рис 2.).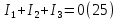 Выразим токи ветвей через потенциалы узлов: 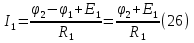 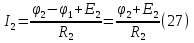 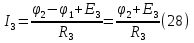 Уравнения (25),(26),(27),(28) следует объединить в систему: 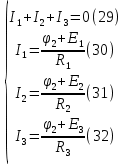 Складывая (30),(31),(32) и учитывая (29) получим: 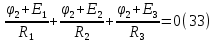 Перепишем уравнение (33) в следующем виде: 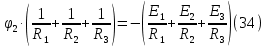 Далее преобразуем уравнение (34) учитывая что: 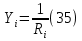 Где 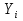 – проводимость – проводимость 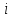 – ой ветви в результате получим. В результате уравнение (34) преобразуется к виду: – ой ветви в результате получим. В результате уравнение (34) преобразуется к виду: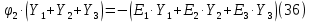 Выражая из (36) 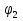 получим: получим: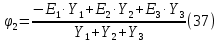 Найдем числовые значения проводимостей ветвей: 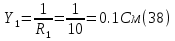 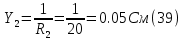 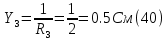 Подставляя числовые значения в (37) находим потенциал 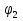 : :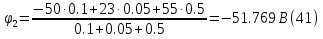 Далее из (30) следует: 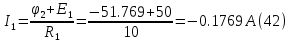 Из (31) следует: 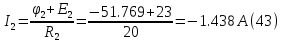 Из (32) следует: 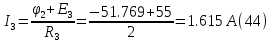 Результаты расчетов токов ветвей по методам контурных токов и узлового напряжения совпадают. Задача 4. В трехфазную цепь с линейным напряжением 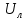 включена трехфазная симметричная нагрузка в звезду или треугольник. В каждой фазе нагрузки последовательно соединены резистор включена трехфазная симметричная нагрузка в звезду или треугольник. В каждой фазе нагрузки последовательно соединены резистор 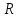 и катушка и катушка 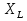 (или конденсатор (или конденсатор 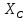 ). ).
Решение Дано: 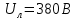 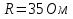 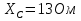
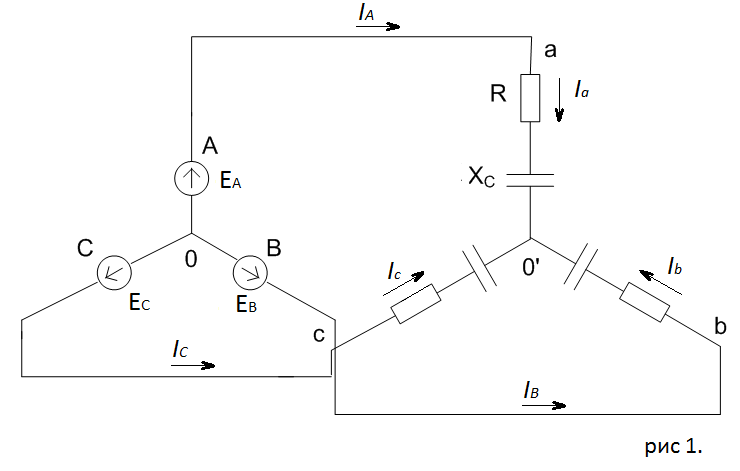
Определяем модуль действующих значений фазных ЭДС. В данном случае нагрузка соединена звездой поэтому имеем: 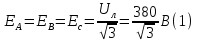 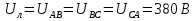 – действующее напряжение между линейными проводами. – действующее напряжение между линейными проводами.Определяем комплексы действующих значений фазных ЭДС: 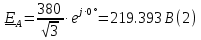 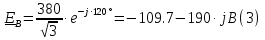 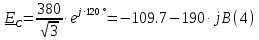 Определяем комплексы фаз нагрузки: 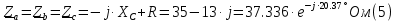 Преобразуем исходную цепь. 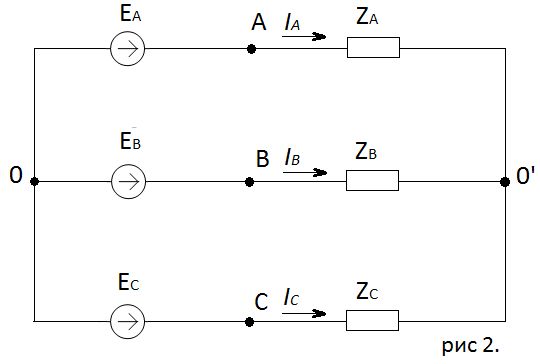 Для полученной схемы имеем: 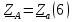 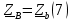 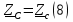 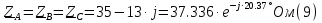 Для цепи с симметричной нагрузкой напряжение смещения нуля нагрузки 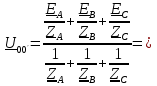 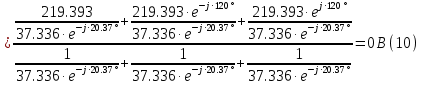 Действующие значения линейных токов и токов фаз нагрузки равны: 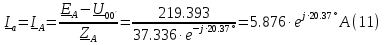 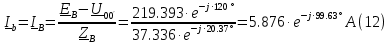 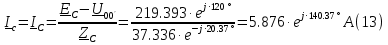 Находим мощность трехфазной системы. Комплекс полной мощности системы равен: 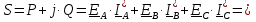 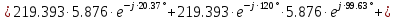 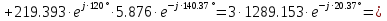 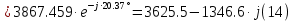 Активная мощность системы равна: 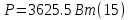 Реактивная мощность системы равна: 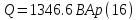 Полная мощность системы равна: 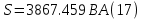 Коэффициент мощности системы: 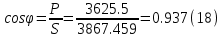
 Задача 5. Трехфазный силовой трансформатор имеет следующие паспортные данные: номинальная мощность 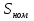 , номинальные линейные напряжения первичной и вторичной обмоток , номинальные линейные напряжения первичной и вторичной обмоток 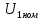 , и , и 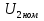 , мощность потерь короткого замыкания , мощность потерь короткого замыкания 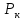 , напряжение короткого замыкания , напряжение короткого замыкания 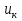 . Известна также схема соединения обмоток. . Известна также схема соединения обмоток.
Указание: мощности потерь в обмотках полагать одинаковыми. Решение Дано: 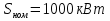 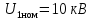 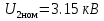 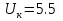 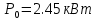 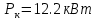 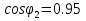 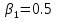 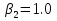 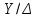
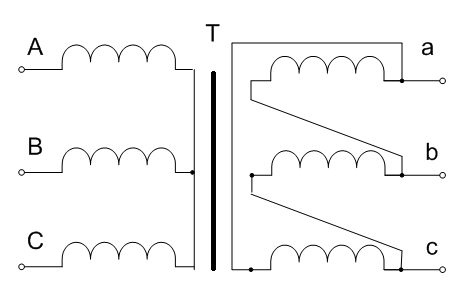
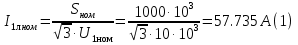  Находим рабочие токи при коэффициентах загрузки 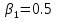 и и 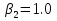 : :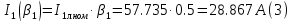 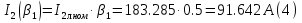 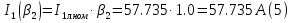 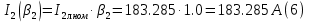 Фазные и линейные токи первичной обмотки равны так она соединяется звездой: 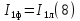 Находим номинальные фазные токи вторичной обмотки: 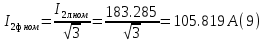 Находим рабочие фазные токи вторичной обмотки: 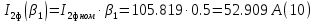 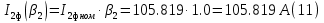 Номинальные фазные напряжения равны: 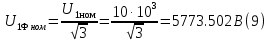 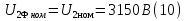 Коэффициент трансформации: 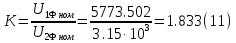 Активное сопротивление короткого замыкания равно: 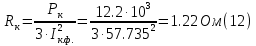 где 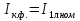 - по условиям опыта короткого замыкания - по условиям опыта короткого замыканияСопротивление первичной обмотки равно: 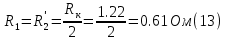 Сопротивление вторичной обмотки равно: 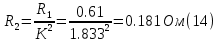 Находим КПД при заданном коэффициенте мощности и коэффициентах нагрузки 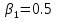 и и 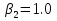 . .Расчет коэффициента полезного действия производим по формуле: 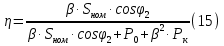 При коэффициенте загрузки 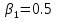 получим: получим: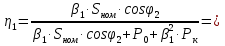 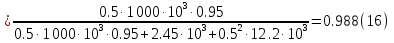 При коэффициенте загрузки 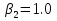 получим: получим: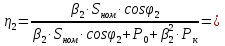 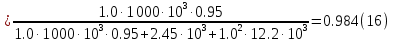
Указание: мощности потерь в обмотках полагать одинаковыми. Находим полное сопротивление короткого замыкания 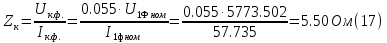 Реактивное сопротивление короткого замыкания 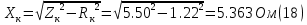 Коэффициент мощности трансформатора в режиме холостого хода: 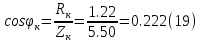 Рассчитаем изменение напряжения на вторичной обмотке трансформатора при активно-индуктивном характере нагрузки с коэффициентом мощности равным 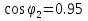 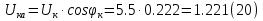 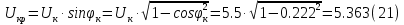 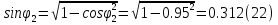 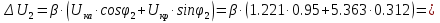 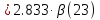 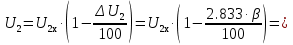 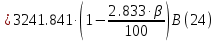 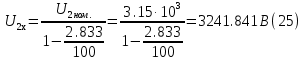 Строим график зависимости 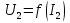 : :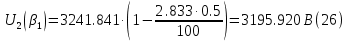 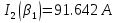 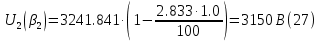 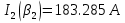 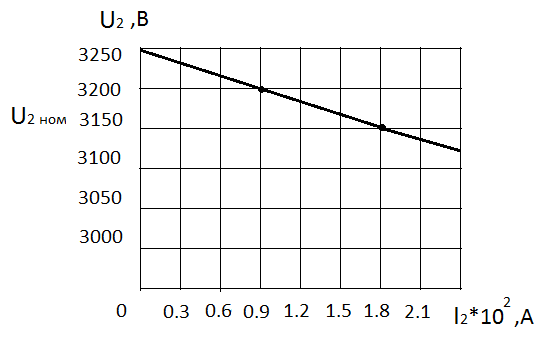 Задача 6. Асинхронный трехфазный двигатель с короткозамкнутым ротором имеет следующие данные: номинальное напряжение 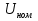 , мощность на валу , мощность на валу 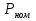 , скольжение , скольжение 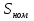 , КПД , КПД 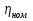 , коэффициент мощности , коэффициент мощности 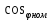 , число пар полюсов , число пар полюсов 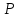 , отношение максимального момента к номинальному , отношение максимального момента к номинальному 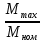 , отношение пускового момента к номинальному , отношение пускового момента к номинальному 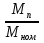 , отношение пускового тока к номинальному , отношение пускового тока к номинальному 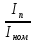 . Частота . Частота 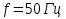 . Известна схема соединения обмоток статора. . Известна схема соединения обмоток статора.
Решение Дано: 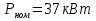 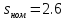 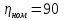 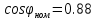 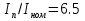 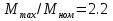 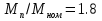 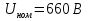 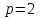 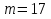 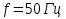 
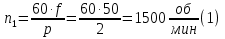 Номинальная частота вращения ротора электродвигателя: 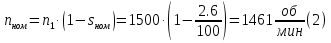 Номинальный вращающий момент двигателя: 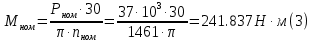 Максимальный момент двигателя: 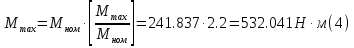 Пусковой момент двигателя: 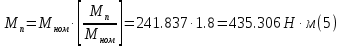 Номинальный линейный ток двигателя: 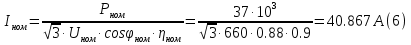 Пусковой линейный ток двигателя: 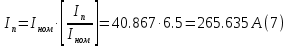 Номинальный фазный ток двигателя при соединении обмоток статора звездой равен линейному току. 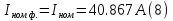 Номинальный фазный пусковой ток двигателя при соединении обмоток статора звездой равен линейному пусковому току. 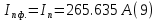

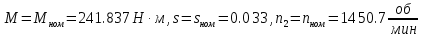
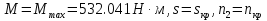
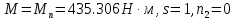 Определим критическое скольжение 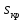 при котором асинхронный двигатель развивает максимальный вращающий момент. при котором асинхронный двигатель развивает максимальный вращающий момент.Используем обозначение 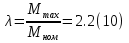 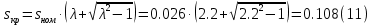 Определим критическую частоту вращения ротора: 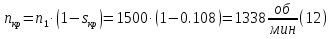 Для расчета промежуточных точек воспользуемся формулой позволяющей определить вращающий момент при любых значениях скольжения. 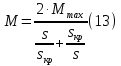 При скольжении 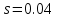 получим: получим: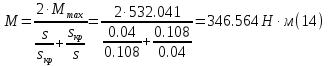 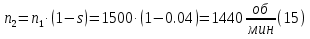 При скольжении 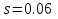 получим: получим: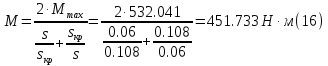 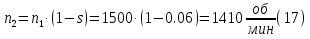 При скольжении 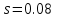 получим: получим: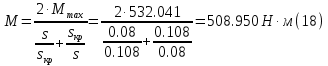 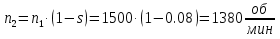 Строим механическую характеристику 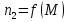 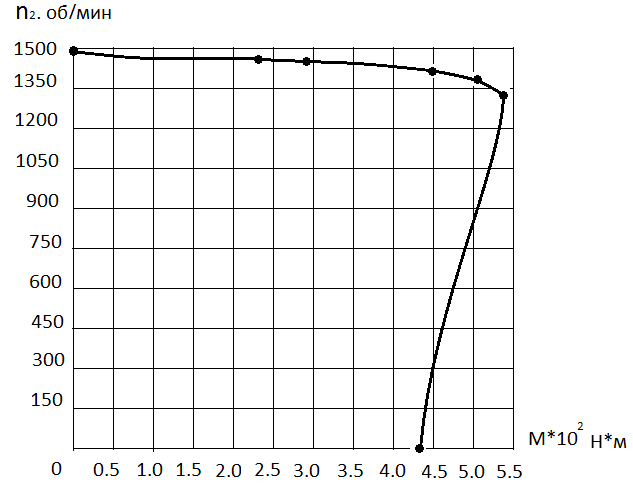
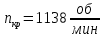 Проверим возможность пуска двигателя при понижении напряжения на 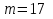 Вращающий момент двигателя пропорционален квадрату напряжения для возможности пуска необходимо выполнение условия: 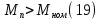 Где 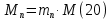 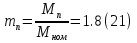 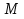 рассчитывается по формуле: рассчитывается по формуле: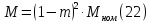 С учетом (20),(21),(22) условие (19) принимает вид: 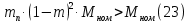 Подставляя в (23) числовые значения получим: 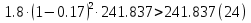 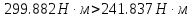 следовательно, пуск двигателя возможен. следовательно, пуск двигателя возможен. |

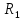 и
и 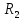 ; КПД при заданном коэффициенте мощности и коэффициентах нагрузки
; КПД при заданном коэффициенте мощности и коэффициентах нагрузки 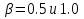 .
.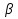 и
и 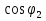 вторичное напряжение
вторичное напряжение 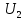 и построить внешнюю характеристику
и построить внешнюю характеристику 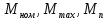 ;
;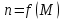 по табличным (каталожным) данным.
по табличным (каталожным) данным.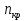 и подсчитать ее критическое скольжение
и подсчитать ее критическое скольжение 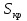 .
.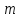 .
.