ЭКЗАМЕН 03.02. Решение де также Sj размеры объединяемых платежей со сроками nj n0

• Название: Решение де также Sj размеры объединяемых платежей со сроками nj n0
• Дата: 04.02.2022
• Размер: 19.48 Kb.
• Имя файла: ЭКЗАМЕН 03.02.docx
• Тип: Решение; #351817

Задача 1

Дано: P = 10 млн.руб., n = 6 лет, i = 10%, n₁ = 1, n₂ = 3, n₃ = 5

Найти: S

Решение: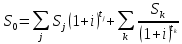



де также Sj — размеры объединяемых платежей со сроками nj < n0, Sk — размеры платежей со сроками nk > n0

В этом случае уравнение эквивалентности удобно составить на момент одного платежа (на конец шестого года).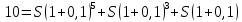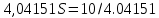





S = 2,47 млн.руб.

Ответ: платеж равен 2,47 млн.руб.
Задача 3

Дано: n = 5 лет, S = 60 тыс.руб., i = 10%, p = 12, R = 1000 руб.

Найти: А

Решение:

Текущую стоимость ренты определим по формуле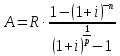



где А –текущая стоимость ренты;

R – размер платежа;

i – процентная ставка;

p – количество платедей в год

n – срок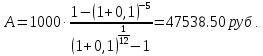



Ответ: сумма равна 47538,50 руб.
Задача 4

Дано: N = 1000 руб., с = 6%, n = 6 лет, r = 9%, r = 8%

Найти: Р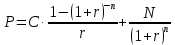



где Р – рыночная цена облигации;

С – купон

r – доходность

n – срок

N – номинальная стоимость облигации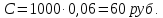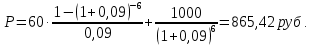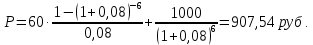







Ответ: таким образом, с изменением доходности с 9% на 8%, рыночная стоимость облигации увеличится с 865,42 руб. до 907,54 руб.
Задача 2

Дано: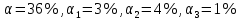

Найти: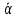

Решение:

Годовой темп инфляции определяется по формуле: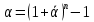



Составим уравнение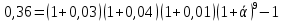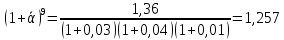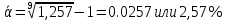







Ответ: среднемесячный темп инфляции за оставшийся период равен 2,57%
Задача 5

Дано: А(0,08;0,08) и В(0,05;0,06), р = 0,2

Найти: Х,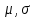

Решение:

Составим ковариационную матрицу. Ее элементы равны: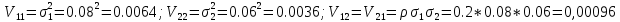



. Ковариационная матрица равна: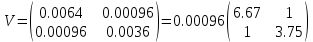



Обратная матрица равна: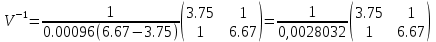