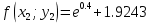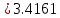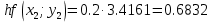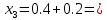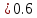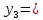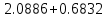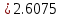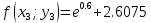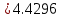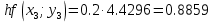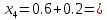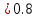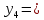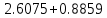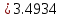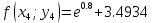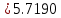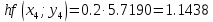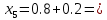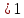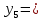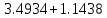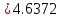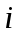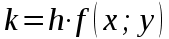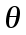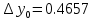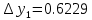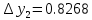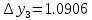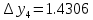Диф уравнения, методы приближенного решения. Приближ ДУ В1 (нов). Решение дифференциального уравнения с начальным условием на отрезке, приняв за шаг
 Скачать 53.55 Kb. Скачать 53.55 Kb.
|
|
Задание. Найти решение дифференциального уравнения 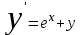 с начальным условием с начальным условием 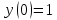 на отрезке на отрезке 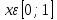 , приняв за шаг , приняв за шаг 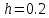 . .Точное решение 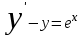 - линейное уравнение. - линейное уравнение.Подстановка: 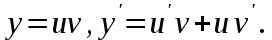 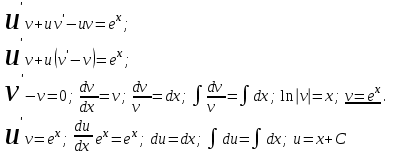 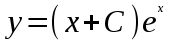 При 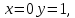 найдем С найдем С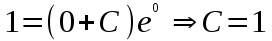 Значит, 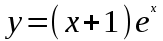 - точное решение дифференциального уравнения. - точное решение дифференциального уравнения.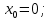 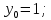 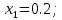 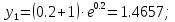 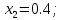 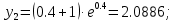 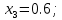 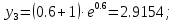 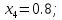 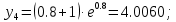 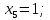 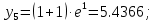 2. Приближенное решение дифференциального уравнения по методу Эйлера Т.к. 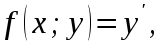 то то 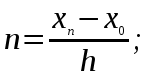 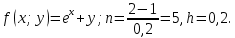
3. Приближенное решение дифференциального уравнения по методу Рунге-Кутта 1) Записываем в первой строке 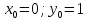 2) Вычисляем 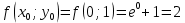 ,тогда ,тогда 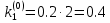 3) Записываем во второй строке: 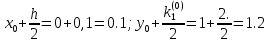 4) Вычисляем: 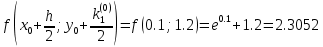 тогда 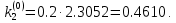 5) Записываем в третьей строке: 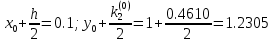 6) Вычисляем 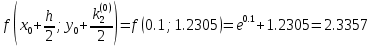 тогда 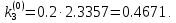 7) Записываем в четвертой строке 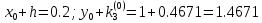 8)Вычисляем 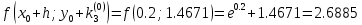 тогда тогда 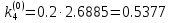 9) В столбце 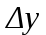 записываем записываем 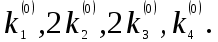 10) Вычисляем 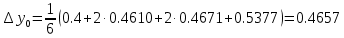 11) Получаем  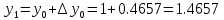 Значения 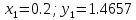 заносим в строку, помеченную индексом заносим в строку, помеченную индексом 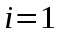 , и снова проводим вычисления по формулам. , и снова проводим вычисления по формулам.
Таблица сравнения методов Эйлера, Рунге-Кутта и точного решения уравнения 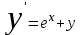 . .
Вывод: анализируя полученные результаты, мы можем сказать, что самым точным из двух методов приближенного решения дифференциального уравнения 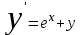 является метод Рунге-Кутта, метод Эйлера дает грубые ошибки. Метод Рунге-Кутта дает практически точное решение дифференциального уравнения, но требует большего объема вычислений, чем предыдущий метод. является метод Рунге-Кутта, метод Эйлера дает грубые ошибки. Метод Рунге-Кутта дает практически точное решение дифференциального уравнения, но требует большего объема вычислений, чем предыдущий метод.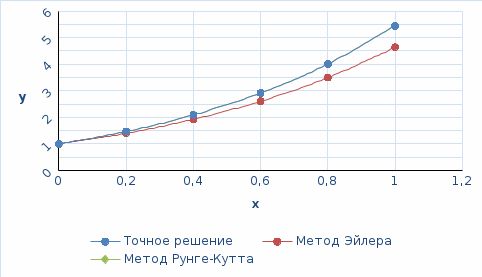 Рисунок 1 – График сравнения методов Эйлера, Рунге-Кутта и точного решения дифференциального уравнения 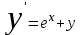 с начальным условием с начальным условием 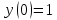 на отрезке на отрезке 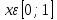 с шаг с шаг 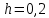 . . |

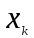
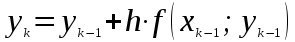
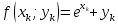
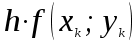
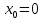
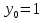
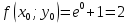
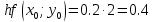
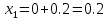
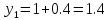
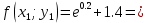
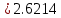
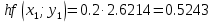
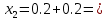
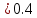
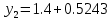
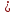 1.9243
1.9243