построить сечение пирамиды. Построить сечение пирамиды SABCD плоскостью. Решение Для начала мы должны построить дополнительную плоскость ast 2, которая будет содержать в себе прямую ар
 Скачать 0.69 Mb. Скачать 0.69 Mb.
|
|
Построить сечение пирамиды SABCD плоскостью, проходящей через прямую QR, где Q лежит на ребре SB, R - на ребре AD и точку P, которая лежит на прямой AK, где точка K лежит в грани SBC и находится между точками A и P. Решить методом следа и методом вспомогательных сечений по отдельности. Решить методом следа Строится линия пересечения (след) секущей плоскости с плоскостью основания многогранника. Находим точки пересечения секущей плоскости с ребрами многогранника. Решение: Для начала мы должны построить дополнительную плоскость AST2 , которая будет содержать в себе прямую АР. 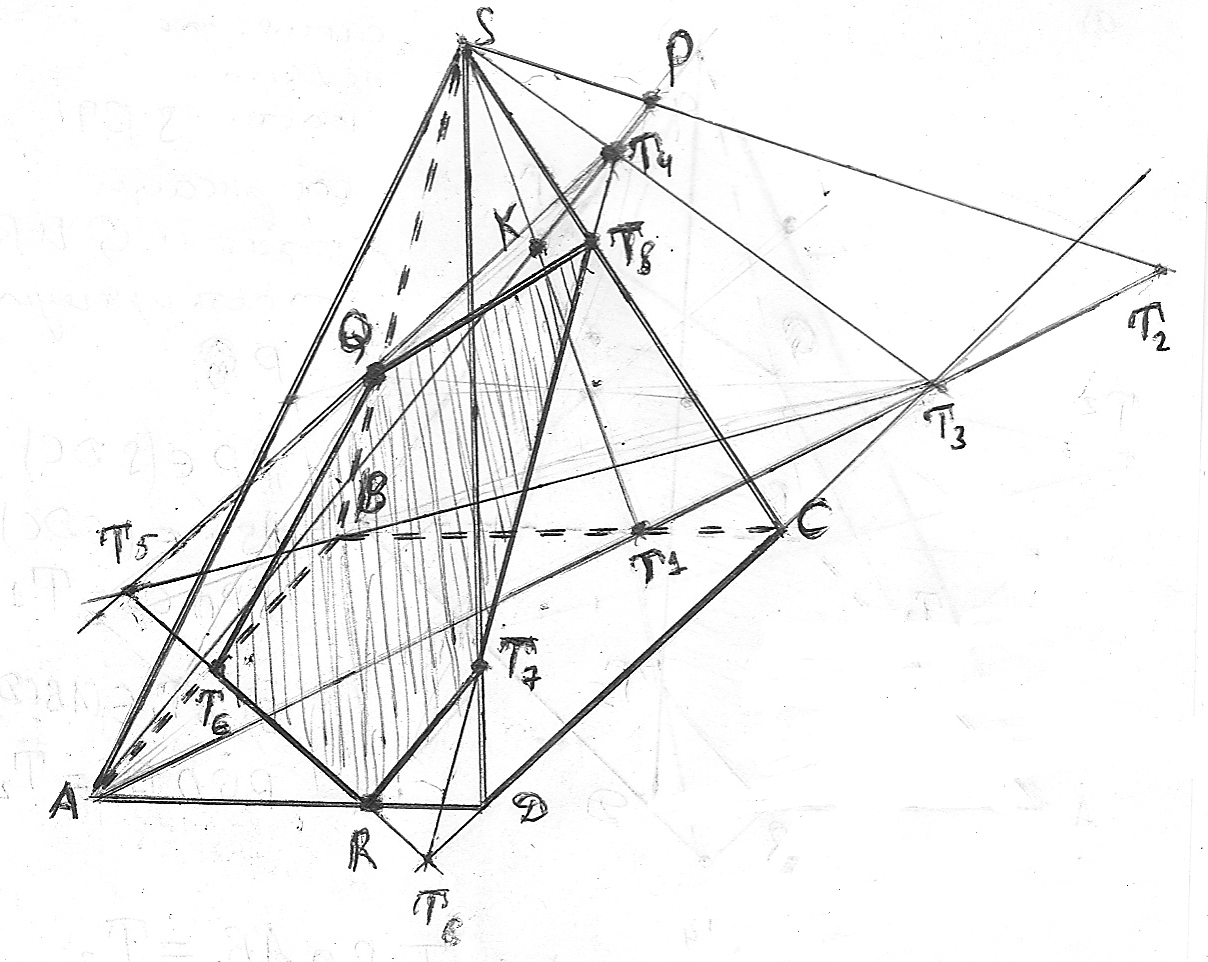 Точка К принадлежит плоскости BSC, то есть запись такая: (  ) K ) K 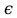 пл. (BSC) пл. (BSC)Прямая SK так же принадлежит плоскости BSC, т.е. SK 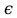 пл. (BSC). Отсюда следует, что прямая SK пересекает прямую BC в точке Т1, то есть пл. (BSC). Отсюда следует, что прямая SK пересекает прямую BC в точке Т1, то есть 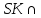 BC в ( BC в ( ) Т1 ) Т1Точки (  ) A, S, P, Т1 принадлежат плоскости (ASТ1), то есть ( ) A, S, P, Т1 принадлежат плоскости (ASТ1), то есть ( ) A, S, P, Т1 ) A, S, P, Т1 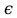 пл. (ASТ1). Значит прямая AТ1 пересекает прямую SP в точке ( пл. (ASТ1). Значит прямая AТ1 пересекает прямую SP в точке ( ) T2. (Запись выглядит следующим образом: AТ1 ) T2. (Запись выглядит следующим образом: AТ1 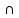 SP в ( SP в ( ) Т2 ) Т2Получается точки (  ) A, Т1, Т2, D, С принадлежат плоскости (ABCD). ( ( ) A, Т1, Т2, D, С принадлежат плоскости (ABCD). ( ( ) A, Т1, Т2, D, С ) A, Т1, Т2, D, С 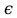 пл. (ABCD). Отсюда получаем, что прямая AТ2 пересекает прямую DС в точке ( пл. (ABCD). Отсюда получаем, что прямая AТ2 пересекает прямую DС в точке ( ) T3. (Запись выглядит следующим образом: AТ2 ) T3. (Запись выглядит следующим образом: AТ2 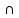 DС в ( DС в ( ) T3. ) T3.Точки (  ) A, S, Т3, K, P принадлежат плоскости (ASТ2). ) A, S, Т3, K, P принадлежат плоскости (ASТ2). Вид записи: (  ) A, S, Т3, K, P ) A, S, Т3, K, P 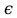 пл. (ASТ2) пл. (ASТ2)Следовательно, прямая AР пересекает прямую SТ3 в точке (  ) T4. (Запись выглядит следующим образом: AР ) T4. (Запись выглядит следующим образом: AР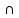 SТ3 в ( SТ3 в ( ) T4. ) T4. Задача решена. Был использован метод следа. |
