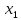автор. Решение Для нахождения оптимума применим необходимое условие экстремума в нашем случае
 Скачать 1.46 Mb.
|
 Решение: Для нахождения оптимума применим необходимое условие экстремума:  В нашем случае:  Из данного следует:      Таким образом, критическая точка, в которой выполняется необходимое условие экстремума имеет координаты: A (0,0).  Рисунок 1 – Расположение критической точки Для проверки наличия экстремума в критической точке, применим метод сканирования. Для этого построим кривые оптимизации, проходящие через критическую точку. В кривой будем изменять значения оптимиз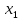ирующего фактора  . Значение оптимизирующего фактора 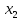 будет фиксированным, то есть для кривой, проходящей через точку А,  . Результаты расчеты точек целевой функции приведены в таблице 1, кривые оптимизации – на рисунке 2.Таблица 1 Результаты расчета целевой функции
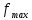    Рисунок 2 – Кривые оптимизации Как видно из рисунка 2, целевая функция имеет максимум  в точке с координатами  . Безусловный минимум отсутствует. | ||||||||||||||
