174923-1 Обухова Практическая часть. Решение Для непрерывных составляющихХиУ математическое ожидание, Получаем

• Название: Решение Для непрерывных составляющихХиУ математическое ожидание, Получаем
• Дата: 10.11.2022
• Размер: 41.23 Kb.
• Имя файла: 174923-1 Обухова Практическая часть.docx
• Тип: Решение; #780584

СОДЕРЖАНИЕ

Задание 1 2

Список использованных источников 4

Задание 1

Условие:

Плотность распределения вероятности системы случайных величин (Х,У)имеет вид: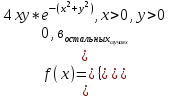

Найдите математическое ожидание и дисперсию координат (случайных величин Х и У) Найдите коэффициент корреляции.
Решение:

Для непрерывных составляющих Х и У математическое ожидание: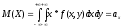

,

Получаем: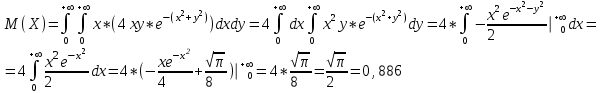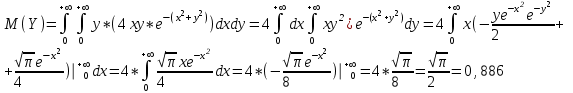





Найдем дисперсию, используя формулу: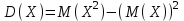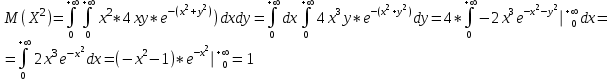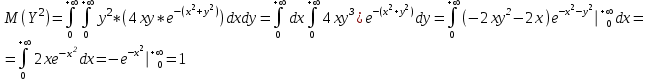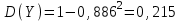











Коэффициент корреляции вычисляется по формуле: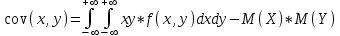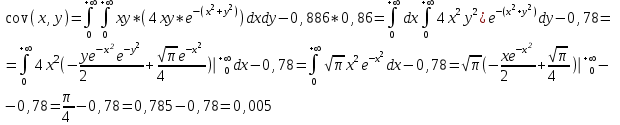







Тогда: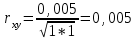

Список использованных источников

1. 
   Бугров, Я.С. Высшая математика в 3 т. Т.1 в 2 книгах. Дифференциальное и интегральное исчисление: Учебник для академического бакалавриата / Я.С. Бугров, С.М. Никольский. - Люберцы: Юрайт, 2016. - 501 c.
   
2. 
   Зельдович, Я.Б. Высшая математика для начинающих физиков и техников / Я.Б. Зельдович, И.М. Яглом. - М.: Ленанд, 2019. - 512 c