Теоретическая механика. Задание 8. Решение. Для определения скорости груза 1 применим теорему об изменении кинетической энергии системы в интегральной форме
 Скачать 165.08 Kb. Скачать 165.08 Kb.
|
 Рисунок 1.8 Рисунок 1.8Задание 8. Вариант 23. Механическая система под действием сил тяжести приходит в движение из состояния покоя. Начальное положение системы показано на схеме. Учитывая трение скольжения тела 1, пренебрегая массами нитей и предполагая их нерастяжимыми, определить скорость тела 1 в тот момент, когда пройденный им путь станет равным S. Дано:  =m, =m, 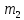 =m, =m,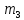 =(1/10)*m, =(1/10)*m, =(4/5)*m, =(4/5)*m, 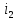 =18см=0.18м, =18см=0.18м, 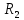 =20см=0.2м, =20см=0.2м, 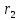 =0.8* =0.8*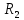 =0.16м, α= =0.16м, α=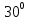 , S=1м, g , S=1м, g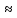 9.81м/ 9.81м/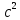 , ,  =0.1. =0.1.Определить: 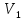 -? -?Решение. Для определения скорости груза 1 применим теорему об изменении кинетической энергии системы в интегральной форме:  Так как система неизменяемая и начинает движение из состояния покоя, то: 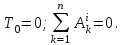 Тогда теорема будет иметь вид: 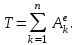 (1) (1)Определим кинетическую энергию системы: 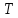 = = + +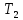 + + + +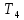 , где , где =0.5* =0.5* * *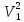 - кинетическая энергия груза 1, совершающего поступательное - кинетическая энергия груза 1, совершающего поступательное движение; 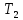 =0.5* =0.5*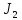 * *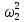 - кинетическая энергия ступенчатого блока 2, совершающего - кинетическая энергия ступенчатого блока 2, совершающего вращательное движение;  =0.5* =0.5*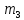 * *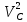 +0.5* +0.5* * *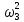 - кинетическая энергия блока 3, совершающего - кинетическая энергия блока 3, совершающего плоскопараллельное движение; 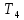 =0.5* =0.5* * *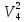 - кинетическая энергия груза 4, совершающего - кинетическая энергия груза 4, совершающегопоступательное движение; Величины 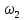 , , 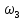 , ,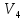 , , 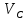 , выражаем через скорость , выражаем через скорость 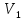 . .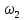 = =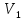 / /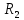 = =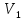 /0.2=5* /0.2=5*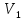 ; ;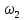 * *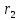 = =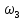 *2* *2*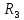 ; ;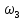 = =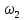 * *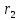 /(2* /(2*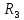 )=5* )=5*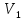 *0.16/(2* *0.16/(2*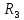 )=0.4* )=0.4*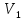 / /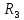 ; ;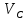 = =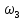 * *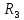 =0.4* =0.4*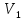 * *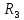 / /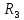 =0.4* =0.4*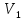 ; ;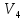 = =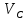 =0.4* =0.4*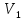 ; ;Итак, 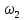 =5* =5*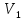 , ,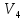 =0.4* =0.4*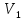 , ,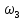 =0.4* =0.4*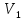 / /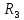 , ,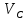 =0.4* =0.4*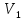 ; ;Моменты инерции блока 3 и блока 2 относительно осей вращения: 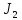 = =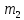 * * =m*0.18*0.18=0.0324*m; =m*0.18*0.18=0.0324*m; =0.5* =0.5*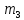 * *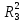 =0.5*(1/10)*m* =0.5*(1/10)*m*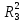 =0.05*m* =0.05*m*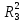 ; ;Получаем выражения кинетических энергий тел:  =0.5* =0.5* * *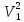 =0.5*m* =0.5*m*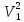 ; ;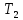 =0.5* =0.5*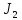 * *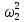 =0.5*0.0324*m*25* =0.5*0.0324*m*25*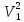 =0.405*m* =0.405*m*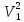 ; ; =0.5* =0.5*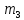 * *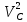 +0.5* +0.5* * *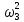 = ==0.5*(1/10)*m*0.16* 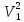 +0.5*0.05*m* +0.5*0.05*m*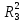 *0.16* *0.16*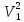 / /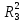 = ==0.008*m* 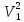 +0.004*m* +0.004*m*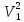 =0.012*m* =0.012*m*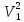 ; ;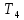 =0.5* =0.5* * *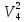 =0.5*(4/5)*m*0.16* =0.5*(4/5)*m*0.16*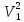 =0.064*m* =0.064*m*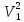 ; ;Кинетическая энергия всей системы: 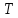 = = + +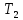 + + + +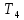 = ==0.5*m* 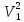 +0.405*m* +0.405*m*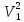 +0.012*m* +0.012*m*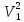 +0.064*m* +0.064*m*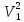 =0.981*m* =0.981*m*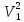 ; ;Итак кинетическая энергия всей системы: T=0.981*m* 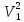 ; (2) ; (2) Определяем работу внешних сил системы на перемещении S. Внешние силы: силы тяжести 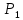 , , , , 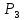 , ,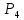 опорные реакции опорные реакции 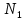 , , 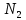 , сила трения , сила трения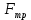 . .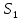 =S=1м; =S=1м; =0.4* =0.4*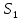 =0.4*1=0.4м; =0.4*1=0.4м; = = =0.4м; =0.4м;Запишем выражения для работ внешних сил системы на её конечном перемещении S: A( 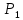 )= )=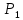 * *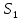 *sinα= *sinα= *g* *g*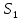 *sinα=m*9.81*1*0.5 *sinα=m*9.81*1*0.5 4.905*m; 4.905*m;A( 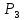 )= )= * * = =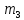 *g* *g* =(1/10)*m*9.81*0.4 =(1/10)*m*9.81*0.4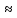 0.3924*m; 0.3924*m;A( 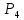 )= )=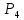 * * = = *g* *g* =(4/5)*m*9.81*0.4 =(4/5)*m*9.81*0.4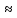 3.1392*m; 3.1392*m;A( 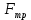 )= )= * *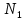 * *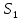 = = * * *g*cosα* *g*cosα*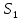 =0.1*m*9.81*0.866*1 =0.1*m*9.81*0.866*1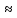 0.8495*m; 0.8495*m;A(  , , 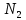 ) =0, так как точка приложения этих сил или неподвижна. ) =0, так как точка приложения этих сил или неподвижна.Сумма работ внешних сил: 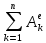 = A( = A(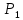 )-A( )-A(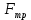 )-A( )-A(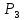 )-A( )-A(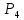 )= )==4.905*m-0.8495*m-0.3924*m-3.1392*m  0.5239*m; 0.5239*m;По теореме об изменении кинетической энергии: T= 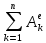 ; ;0.981*m* 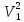 =0.5239*m; =0.5239*m;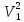 =0.5239*m/(0.981*m) =0.5239*m/(0.981*m)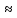 0.53404689; 0.53404689;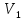 = = 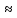 0.73м/с; 0.73м/с;Ответ: 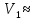 0.73м/с. 0.73м/с. |
