Горбатенко переписать в тетр. Решение Доходность за период t t 1 t 2 равна по формуле
 Скачать 124.39 Kb. Скачать 124.39 Kb.
|
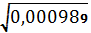 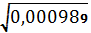 5 вариант 5 вариант1. Пусть доходности за два последовательных периода времени t1 и t2 равны 12% и 16 % соответственно. Определить доходность за период t = t1 + t2 . Решение: Доходность µ за период t= t1 + t2 равна по формуле: µ = µ1+ µ2+ µ1+ µ2 =0,12+0,16+0,12*0,16=0,2992 то есть 29,92 % 2. Доходность актива за месяц равна 2,5%. Найти доходность актива за год при условии, что месячная доходность в течение года постоянна. Решение: Будем применять формулу: µ= (1+ µ1)n-1 µ= (1+ µ1)n-1 = (1+0,025)12-1=0,344=34,4% Ответ: 34,4% 3. Доходность актива за год равна 25%. Найдите доходность актива за месяц, предполагая ее постоянство. Решение: Дано µ = 0,25 n = 12 µ1 =? µ= (1+ µ1)n-1 (1+ µ1)n= µ+1 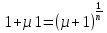 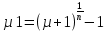 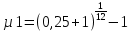 =1,9 % =1,9 %Ответ: 1,9% 4. Пусть матрица последствий есть 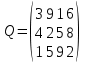 Составить матрицу рисков. Для нахождения рисков - в каждом столбце выбирается максимальное значение дохода и из него вычитаются остальные значения этого столбца. Решение: Найдём максимальный элемент в каждом столбце: 4,9,9,8. Матрица рисков: 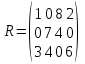 5. Для матрицы последствий 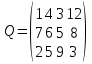 выберите вариант решения: А) по критерию максимакса Б) по критерию Вальда (максимина) В) по критерию Сэвиджа Г) по критерию Гурвица при λ =1/2. Решение: А) по критерию максимакса Находим последовательность значений : a1=12, a2=8, a3=9, (max в каждой строке). Из этих значений находим наибольшее: a1=12. Следовательно, критерий максимакса рекомендует принять второе решение (i=1). Б) по критерию Вальда (максимина) bi = min qij b1 = 1, b2 = 5, b3 = 2, (min в каждой строке). Из этих значений выбираем максимальное: b2 = 5. Значит, правило Вальда рекомендует принять 2-е решение (i=5). В) по критерию Сэвиджа 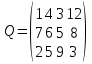 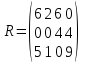 Рассматривая матрицу рисков R, находим последовательность величин ri = r1 = 6, r2 = 4, r3 = 9, (max в каждой строке). Из этих величин выбираем наименьшую: r2 = 4. Значит, правило Сэвиджа рекомендует принять 2-е решение (i=4). Г) по критерию Гурвица при λ =1/2. Рассматривая матрицу последствий Q по строкам, для каждого i вычисляем значения ci= 1/2minqij + 1/2maxqij. с1=1/2*1+1/2*12=6,5; с2=1/2*5+1/2*8=6,5; с3=1/2*2+1/2*9=5,5. Наибольшими являются с1=6,5 и с2=6,5. Следовательно, критерий Гурвица при заданном λ =1/2 рекомендует выбрать второй вариант (i=1 и i=2 ). 6. Для матрицы последствий 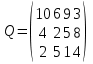 известны вероятности развития реальной ситуации по каждому из четырех вариантов: p1 =0,35, p2=0,35, p3=0,1, p4=0,2. Выяснить: 1. при каком варианте решения достигается наибольший средний доход и какова величина этого дохода; 2. при каком варианте решения достигается наименьший средний ожидаемый риск, и найти величину минимального среднего ожидаемого риска (проигрыша); 3. Используя критерий Лапласа выбрать наилучший вариант решения на основе правила максимизации среднего ожидаемого дохода. Решение: 1. при каком варианте решения достигается наибольший средний доход и какова величина этого дохода. Найдем для каждого i-го варианта решения средний ожидаемый доход: 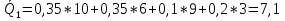 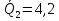 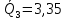 Максимальный средний ожидаемый доход равен 7,1 и соответствует первому решению. 2. при каком варианте решения достигается наименьший средний ожидаемый риск, и найти величину минимального среднего ожидаемого риска (проигрыша); Сперва найдём матрицу рисков: 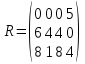 Для каждого i-го варианта решения найдем величину среднего ожидаемого риска. 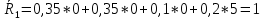 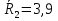 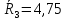 Следовательно, минимальный средний ожидаемый риск равен 1 и соответствует первому решению: = 1. 3. Используя критерий Лапласа выбрать наилучший вариант решения на основе правила максимизации среднего ожидаемого дохода. Средние ожидаемые доходы с учетом равновероятности вариантов реальной ситуации: 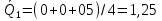 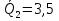 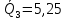 Следовательно, наилучшим вариантом решения будет третий, и максимальный средний ожидаемый доход будет равен 5,25. 7. Портфель состоит из трех видов акций (А, В и С), данные о которых приведены в таблице. Найти доходность портфеля.
Решение: Найдём доходность каждой бумаги: m1=(100-65)/65 = 0,538 m2=(40-55)/55 = -0,273 m3=(450-400)/400 = 0,125 Найдём долю каждой бумаги в портфеле: Стоимость всех бумаг: 150*65+100*55+250*400= 115 250 Доли бумаг: х1=(150*65)/115 250=0,085 х2=(100*55)/ 115 250= 0,048 х3=(250*400)/115 250= 0,868 Доходность портфеля: mp=∑xi mi=x1m1+x2m2+x3m3 = 0,085*0,538+0,048* (-0,273)+ 0,868* 0,125 =0,046-0,013+0,109=0,142=14% 8. В табл. приведены данные о доходности двух бумаг за 5 лет
1) Определить значение ковариации для двух ценных бумаг А и Б. 2) Определить коэффициент корреляции между доходностями этих бумаг. 3) Определить риск портфеля, если доли ценных бумаг одинаковы. Решение:
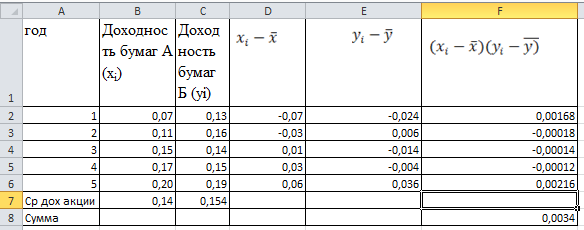 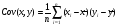 COV = 0,0034/5=0,00068 2) Определить коэффициент корреляции между доходностями этих бумаг. Коэффициент корреляции между доходностями rij=COVij/σi*σj Среднеквадратическое отклонение: 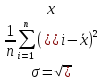 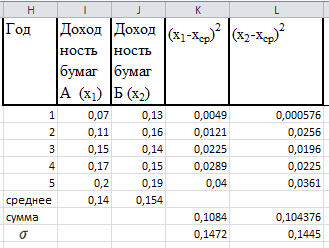 rij=COVij/σi*σj =0,00068/0,1472*0,1445 = 0,0006675272 коэффициент корреляции 3) Определить риск портфеля, если доли ценных бумаг одинаковы. p= 0,0462*0,52+2*0,5*0,5*0,046*0,021*0,724+0,0212*0,52=0,000989 p== 0,0314 9. Сформировать портфель минимального риска из двух видов ценных бумаг: «А» с эффективностью15% и риском 21, и «Б» с эффективностью 6% и риском 7. При условии, что обеспечивается доходность портфеля не менее 8%. Коэффициент корреляции равен 0.4 Решение: Дано: m1= 0,15 m2=0,06 σ1=21 σ2=7 mp>=0,08 r= 0,4 Найти: x1;x2 Модель Марктовица может быть сформулирована следующим образом. Необходимо найти вектор Х=( x1;x2), минимизирующий риск портфеля σр. x1-доля в портфеле ценных бумаг А; x2 - доля в портфеле ценных бумаг Б, 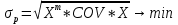 При ограничениях: x1+ x2=1 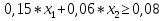 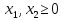 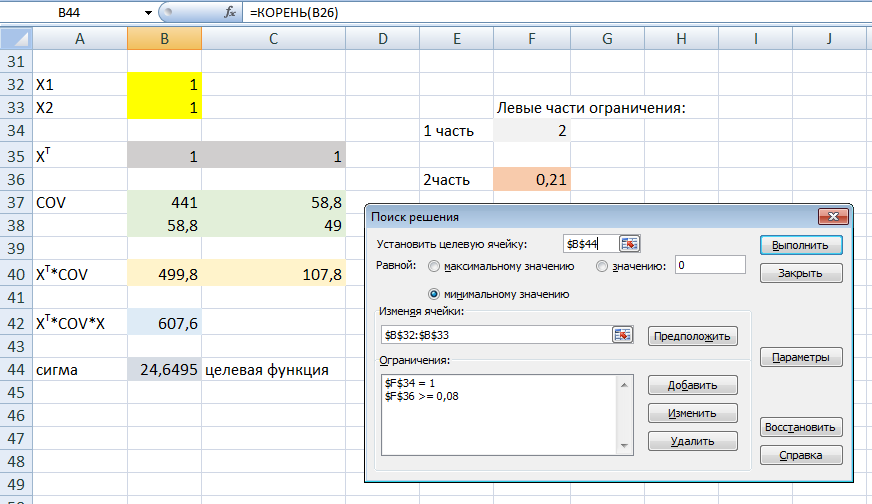  Ответ: доходность бумаги А = 0,22222%, БУМАГИ б=0,77778% 10. Купонный доход 12-летней облигации номиналом 2500 руб. равен 14 % годовых (выплаты в конце года). Найти средний срок поступления дохода от облигации. Решение: 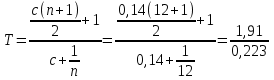 =8,57 ≈ 9 лет =8,57 ≈ 9 лет |
