вар9. Решение Энергия, полученная приемником от солнца через гелиостаты (Вт), может быть определена по уравнению q r г
 Скачать 82.11 Kb. Скачать 82.11 Kb.
|
|
Вариант 9 Задача №1 На солнечной электростанции башенного типа установлено п=323 гелиостатов, каждый из которых имеет поверхность Fг=40 м2. Гелиостаты отражают солнечные лучи на приемник, на поверхности которого зарегистрирована максимальная энергетическая освещенность Н пр = 2,5 МВт/мг. Коэффициент отражения гелиостата Rг =0,8. коэффициент поглощения приемника Апр =0,95. Максимальная облученность зеркала гелиостата Hг=600 Вт/м2 . Определить площадь поверхности приемника Fпр и тепловые потери в нем, вызванные излучением и конвекцией, если рабочая температура теплоносителя составляет t=520 °С. Степень черноты приемника епр =0,95. Конвективные потери вдвое меньше потерь от излучения.
Энергия, полученная приемником от солнца через гелиостаты (Вт), может быть определена по уравнению: Q = Rг·Апр·Fг Нг ·п = =0,8·0,95·40·600·323=5891520 Вт где Нг - облученность зеркала гелиостата в Вт/м2 Fг- площадь поверхности гелиостата, м2; п - количество гелиостатов; Rг - коэффициент отражения зеркала концентратора, Aпр - коэффициент поглощения приемника Площадь поверхности приемника может быть определена, если известна энергетическая освещенность на нем Нпр Вт/ м2 , Fпр=Q/Hпр=5891520/2500000=2,357 м2 В общем случае температура на поверхности приемника может достигать tпов= 1160 К, что позволяет нагреть теплоноситель до 700 оС. Потери тепла за счет излучения в теплоприемнике можно вычислить по закону Стефана-Больцмана: 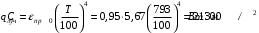 где T - абсолютная температура теплоносителя, К; епр - степень черноты серого тела приемника; Co - коэффициент излучения абсолютно черного тела, Вт / (м2·K4) 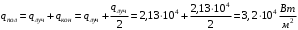 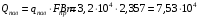 Ответ: Площадь поверхности приемника Fпр=2,357 м2, тепловые потери, вызванные излучением и конвекцией 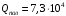 Вт ВтЗадача №2 Считается, что действительный КПД ηдейств океанической ТЭС, использующей температурный перепад поверхностных и глубинных вод (T1-T2)= ∆T и работающей по циклу Ренкина, вдвое меньше термического КПД установки, работающей по циклу Карно, ηtk. Оценить возможную величину действительного КПД ОТЭС, рабочим телом которой является аммиак, если температура воды на поверхности океана t1= 21 °С, а температура воды на глубине океана t2= 4 °С. Какой расход теплой воды V, м3/c потребуется для ОТЭС мощностью N= 2 МВт ? Считать, что плотность воды ρ= 1·10 3 кг/м3 , а удельная массовая теплоемкость Сp = 4,2·103 Дж/(кг-К).
Разность температур поверхностных и глубинных вод: ∆T = T1-T2 = 294-277=17 K. Термического КПД установки, работающей по циклу Карно, ηtk: ηtk=(∆T)/T1= 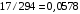 . .В идеальном теоретическом цикле Карно механическая мощность N0 (Вт) может быть определена как: N0=ηtk·Qo Реальный КПД установки, работающей по циклу Ренкина (по условию): ηдейств=0,5· ηtk=0,5·0,0578=0,0289 Механическая мощность N (Вт) в установке, работающей по циклу Ренкина: N= ηдейств ·Qo Тепловую мощность Qo (Вт), полученную от теплой воды можно представить как: 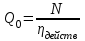 = =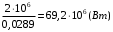 =69,2 МВт =69,2 МВтили как Q0=p·V·Cp·∆T, отсюда расход теплой воды V: 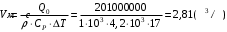 Ответ: действительного КПД ОТЭС ηдейств=2,89 %, расход теплой воды V = 2,81 м3/c Задача №3 Определить начальную температуру t2 и количество геотермальной энергии Еo (Дж) водоносного пласта толщиной h=0,6 км при глубине залегания z=3,5 км, если заданы характеристики породы пласта: плотность ргр = 2700 кг/ м3 ; пористость а = 5 %; удельная теплоемкость Сгр =840 Дж/(кг· К). Температурный градиент (dT/dz) =35 °С /км Среднюю температуру поверхности to принять равной 10 °С. Удельная теплоемкость воды Св = 4200 Дж/(кг · К); плотность воды ρ= 1·103 кг/м3 . Расчет произвести по отношению к площади поверхности F = 1 км2. Минимально допустимую температуру пласта принять равной t1 =40 ° С. Определить также постоянную времени извлечения тепловой энергии τo(лет) при закачивании воды в пласт и расходе ее V =0,1 м3/(с·км2). Какова будет тепловая мощность, извлекаемая первоначально (dE/dτ)τ=0 и через 10 лет (dE/dτ)τ=10 ?
Определим температуру водоносного пласта перед началом его эксплуатации: T2=To+(dT/dz)·z=10+35·3,5=132,5 °С=405,5 K [°С+ 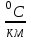 ·км]= [°С] ·км]= [°С]Теплоемкость пласта Спл (Дж/К) можно определить по уравнению: Cпл=[α·ρв·Cв+(1-α)·ρгр·Cгр]·h·F= =[0,05·1·103·4200+(1-0,05)· 2,7·103·840]· 600·1·106=(210000+2154600)· 600·1·106= =141876·1010 Дж/К=1,4·10 15 Дж/К [ 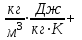 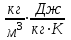 ]·м·м2=[Дж/К] ]·м·м2=[Дж/К]Тепловая мощность, извлекаемая первоначально Еo (Дж): E0=Cпл·(T2-T1)= 189168·1010 ·(405,5-313)= =18798570· 1010 Дж= 1,9·10 17 Дж [ 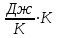 ]=Дж ]=ДжПостоянную времени пласта τ0 (возможное время его использования, лет) в случае отвода тепловой энергии путем закачки в него воды с объемным расходом V (м3/с) можно определить по уравнению: τ0=Cпл/(V·ρв·Св) = 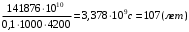 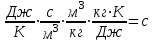 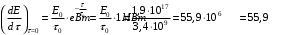 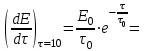 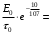 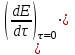 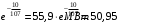 Ответ: начальная температура t2 = 132,5 °С, тепловой потенциал к началу эксплуатации Еo=1,9· 10 17 Дж, возможное время использования пласта τ0=107 лет; тепловая мощность, извлекаемая первоначально 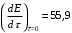 МВт, через 10 лет МВт, через 10 лет 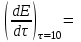 50,95 МВт 50,95 МВтЗадача №4 Определить объем биогазогенератора Vб и суточный выход биогаза Vг в установке, утилизирующей навоз от n=10 коров, а также обеспечиваемую ею тепловую мощность N (Вт). Время цикла сбраживания τ = 14 сут при температуре t = 25 ° С; подача сухого сбраживаемого материала от одного животного идет со скоростью W = 2 кг/сут; выход биогаза из сухой массы νг= 0,24 м3 /кг . Содержание метана в биогазе составляет 70 %. КПД горелочного устройства η=0,6. Плотность сухого материала, распределенного в массе биогазогенератора, р сух ≈50 кг/мг . Теплота сгорания метана при нормальных физических условиях Qнр =28 МДж/м3.
Подача сухого сбраживаемого материала от 10 животных идет со скоростью m0 ( кг/сут): m0=W·n=2·10=20 кг/сут; Cуточный объем жидкой массы Vсут, поступающей в биогазогенерагор (м3/сут) можно определить по формуле: Vсут=m0/ρсух=20/50=0,4 м3/сут Объем биогазогенератора, необходимого для фермы (м3): Vб=τ·Vсут =14·0,4=5,6 м3 Суточный выход биогаза: Vг=m0·ν г =20·0,24=4,8 м3/сут Тепловая мощность устройства, использующего биогаз (МДж/сут): N=η·Qнр·Vг·ƒм = 0,6·28·4,8·0,70= 56,5 МДж/сут. Ответ: объем биогазогенератора Vб=5,6 м3, суточный выход биогаза Vг =4,8 м3/сут, тепловая мощность устройства, использующего биогаз N =56,5 МДж/сут. Задача №5 Для отопления дома в течение суток потребуется Q=0,6 ГДж теплоты. При использовании для этой цели солнечной энергии тепловая энергия может быть запасена в водяном аккумуляторе. Допустим, что температура горячей воды t1=52 ° С. Какова должна быть емкость бака аккумулятора V (м3), если тепловая энергия может использоваться в отопительных целях до тех пор, пока температура воды не понизится до t2=28°C? Величины теплоемкости и плотности воды взять из справочной литературы.
Количество теплоты для отопления дома рассчитывается по формуле: 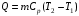 , где ср – теплоемкость теплоносителя (воды); , где ср – теплоемкость теплоносителя (воды); 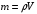 - масса воды - масса водыЕмкость бака аккумулятора 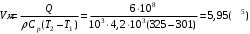 Ответ: емкость бака аккумулятора V=5,95 м3. Задача №6 Используя формулу Л. Б. Бернштейна, оценить приливный потенциал бассейна Э пот (кВт·ч), если его площадь F=3500 км2, а средняя величина прилива Rср =5,2м.
Приливный потенциал бассейна Э пот (кВт·ч): Эпот =1,97·106·R2ср·F = 1,97·106·5,22·3500 = = 186·109 кВт·ч. Ответ: приливный потенциал бассейна Э пот = 186·109 кВт·ч. Задача №7 Как изменится мощность малой ГЭС, если напор водохранилища Н в засушливый период уменьшится в n=3 раза, а расход воды V сократится на m=40 % Потери в гидротехнических сооружениях, водоводах, турбинах и генераторах считать постоянными.
Мощность ГЭС (Вт) можно определить по простому уравнению: N=9,81·V·H·η. Пусть N – мощность малой ГЭС. Известно, что напор водохранилища H в засушливый период уменьшится в 3 раза, а расход воды V сократится на 40 %, то есть Vзас=0,6·V, Hзас = H/3. 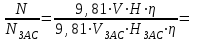 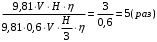 Ответ: мощность малой ГЭС в засушливый период уменьшится в 5 раз. |
