Аналитическая геометрия. Домашнее задание. ДЗ по аналитической геометрии. Решение. Формула уравнения прямой по двум точкам имеет вид, где по условию. Уравнение приобретает вид
 Скачать 0.53 Mb. Скачать 0.53 Mb.
|
Задача 1Запишите уравнение прямой, проходящей через точки M1(−1, 2) и M2(−3,−2). Найдите значения параметров k и b для этой прямой. Решение. Формула уравнения прямой по двум точкам имеет вид:  , ,где по условию  . .Уравнение приобретает вид: 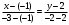 , ,выполнение преобразований:     , ,таким образом, получено уравнение прямой в общем виде: 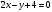 , ,откуда возможен переход к уравнению прямой с угловым коэффициентом: 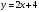 , ,где  Ответ: 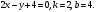 Задача 2. Две стороны квадрата лежат на прямых 5x − 12y − 65 = 0 и 5x − 12y + 26 = 0. Вычислите его площадь. Решение. Так как коэффициенты А и В в данных уравнениях прямых равны, то прямые параллельны. Найдем расстояние L между прямыми по формуле: 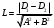 , ,где 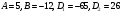 , ,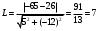 , ,откуда искомая площадь квадрата:  . .Ответ: 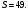 Задача 3Запишите общее уравнение плоскости, проходящей через перпендикуляры, опущенные из точки P(−3, 2, 5) на плоскости 4x + y − 3z + 13 = 0 и x − 2y + z − 11 = 0. Решение. Уравнение плоскости, проходящей через точку и два неколлинеарных вектора имеет вид:  , , где  координаты точки, координаты точки, 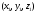 , ,  - координаты векторов. В качестве перпендикуляров подойдут нормальные вектора к заданным плоскостям. - координаты векторов. В качестве перпендикуляров подойдут нормальные вектора к заданным плоскостям.Находим: 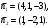 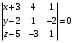 , ,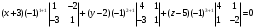 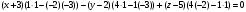 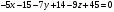 Искомое уравнение плоскости:  . .Ответ:  . .Задача 4. Найдите длину Λ отрезка прямой, параллельной вектору l = (0, 3, 4), между точками пересечения её с плоскостями 2x + y − z − 6 = 0 и 2x + y − z − 4 = 0. Решение. Расстояние между плоскостями вычисляется по формуле:  , , . .Косинус угла между нормалью плоскости  и направляющим вектором прямой и направляющим вектором прямой  можно найти, воспользовавшись скалярным произведением векторов: можно найти, воспользовавшись скалярным произведением векторов: , ,теперь длина отрезка прямой между точками пересечения её с плоскостями:   Ответ: Λ = 10. Ответ: Λ = 10.Задача 5. Найдите те значения m и n, при которых прямая 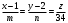 пересекает прямые пересекает прямые  и и 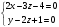 . .Решение. Равенство 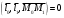 является условием пересечения двух прямых. Искомый направляющий вектор прямой является условием пересечения двух прямых. Искомый направляющий вектор прямой 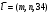 , принадлежащая ей точка: , принадлежащая ей точка: 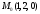 . Находим направляюще векторы . Находим направляюще векторы 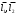 прямых: прямых:      Найдем точки М1, М2, принадлежащие прямым: положим y = 0:   , ,точка М2(2,-1,0), вектор 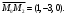 Вычисляем смешанное произведение  : : Вычисляем смешанное произведение  : : Значения m и n найдем, решая систему:  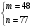 . .Ответ:  Задача 6. Дано, что прямая L, пересекающая ось аппликат в точке  , , 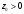 , параллельна плоскости 2x + 3y + 6z + 7 = 0, отстоит от неё на расстоянии 7 и перпендикулярна оси ординат. Найдите абсциссу точки пересечения этой прямой с координатной плоскостью z = 0. , параллельна плоскости 2x + 3y + 6z + 7 = 0, отстоит от неё на расстоянии 7 и перпендикулярна оси ординат. Найдите абсциссу точки пересечения этой прямой с координатной плоскостью z = 0.Решение. Обозначим направляющий вектор  прямой L. По условию прямой L. По условию 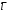 параллелен плоскости, а значит перпендикулярен вектору нормали параллелен плоскости, а значит перпендикулярен вектору нормали  плоскости. Также вектор плоскости. Также вектор 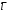 перпендикулярен оси ординат, т.е. вектору перпендикулярен оси ординат, т.е. вектору  . Согласно условиям, решаем систему уравнений: . Согласно условиям, решаем систему уравнений: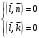 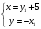 , ,определяющее поворот осей на 270о (против часовой стрелки) и перенос начала координат. В новой системе координат  уравнение кривой принимает канонический вид: уравнение кривой принимает канонический вид: , , определяющее параболу. Координаты вершины параболы получим из формул преобразования координат при 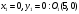 . . Так как  , параметр , параметр . . Ось симметрии параболы совпадает с осью 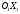 , уравнение оси симметрии получим из формул преобразования координат при , уравнение оси симметрии получим из формул преобразования координат при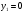 , ,  , ,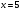 . .Ответ: 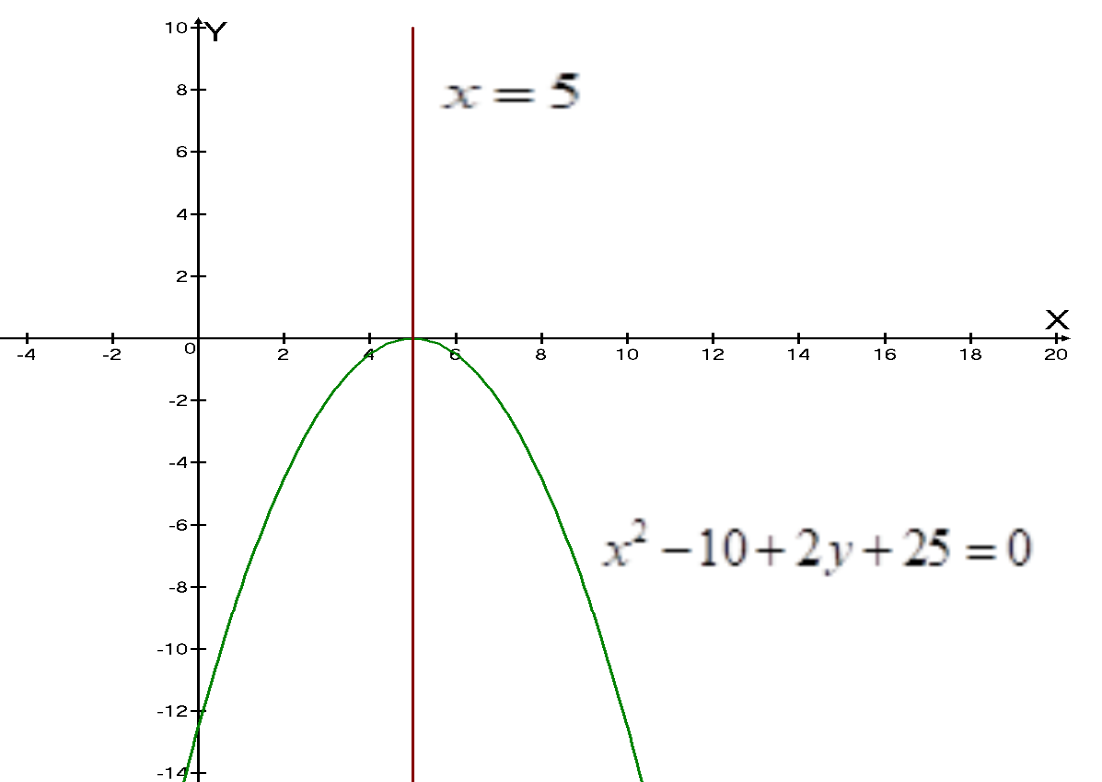 Задача 10Дана кривая 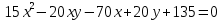 . Докажите, что эта кривая – гипербола. Найдите координаты её центра симметрии. Найдите действительную и мнимую полуоси. Запишите общее уравнение фокальной оси. Постройте данную гиперболу. . Докажите, что эта кривая – гипербола. Найдите координаты её центра симметрии. Найдите действительную и мнимую полуоси. Запишите общее уравнение фокальной оси. Постройте данную гиперболу. Решение. Будем считать, что уравнение кривой задано относительно правой декартовой системы координат OXY с базисом i, j. Приводим квадратичную форму  к главным осям. к главным осям.Определяем коэффициенты  . Тогда матрица квадратичной формы имеет вид: . Тогда матрица квадратичной формы имеет вид:  . .Характеристическое уравнение этой матрицы:   , ,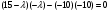 , ,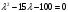 . .Корни характеристического уравнения 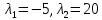 являются собственными числами. являются собственными числами.Так как 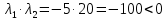 , то это кривая гиперболического типа. , то это кривая гиперболического типа.Канонический вид квадратичной формы:  . .Находим собственные векторы. Для числа 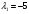 : :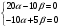   . .Положим 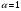 , тогда , тогда  , получен собственный вектор (1,2), его модуль , получен собственный вектор (1,2), его модуль  . Орт собственного вектора, являющийся новым базисным вектором . Орт собственного вектора, являющийся новым базисным вектором 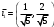 . Новый базис должен быть правым, поэтому . Новый базис должен быть правым, поэтому 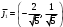 . . Матрица Q перехода от базиса  к к 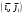 : : , , 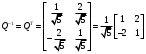 . .Новые коэффициенты линейной формы:  Новая систем координат с базисом  будет будет 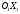 , исходная с базисом , исходная с базисом  - - 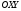 . Выразим новые координаты . Выразим новые координаты 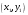 через исходные через исходные 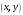 : :  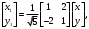 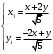 . .Новое уравнение в системе координат 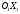 принимает вид: принимает вид: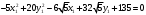 Выполняем преобразования:  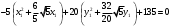 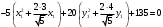    . .В полученном уравнении знак "−" находится при координате 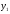 , как и в каноническом уравнении гиперболы. Это означает, что действительная полуось параллельна вектору , как и в каноническом уравнении гиперболы. Это означает, что действительная полуось параллельна вектору 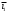 , а мнимая - , а мнимая -  . Следовательно, осталось выполнить перенос начала координат в точку . Следовательно, осталось выполнить перенос начала координат в точку  по формулам: по формулам: В новой системе координат 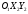 c базисом c базисом  и началом в точке и началом в точке  гипербола имеет каноническое уравнение гипербола имеет каноническое уравнение  . Видим, что действительная полуось . Видим, что действительная полуось  , мнимая полуось , мнимая полуось  . .Центр симметрии гиперболы находится в точке  с координатами с координатами  , или , или 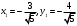 . .Найдем координаты  в системе в системе 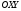 : :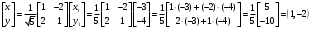 , ,получены координаты точки  . .Запишем уравнения осей  , ,  - выражаем координаты - выражаем координаты  через через  : : . .Ось 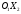 имеет уравнение имеет уравнение 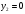 . Подставляя . Подставляя 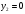 получим получим 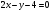 . .Уравнение оси  при при 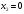 имеет вид имеет вид 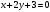 . .Фокальной осью является ось 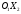 , её уравнение: , её уравнение: 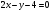 . .Построение: Строим в исходной системе координат 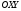 новую систему новую систему 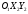 . Обозначаем точку . Обозначаем точку  , проводим оси , проводим оси 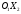 и и  . . Фокальная ось гиперболы совпадает с осью 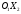 , обозначаем на ней вершины гиперболы: , обозначаем на ней вершины гиперболы:  . .По оси  от точки от точки  откладываем мнимые полуоси: откладываем мнимые полуоси: 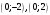 . .Строим прямоугольник, проводя линии, параллельные новым осям координат, через отмеченные точки. Прямые 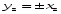 являются асимптотами гиперболы. Они проходят через вершины прямоугольника. являются асимптотами гиперболы. Они проходят через вершины прямоугольника.Используя вершины, прямоугольник и асимптоты, строим данную гиперболу.  Ответ:  ; ; 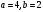 ; ; 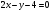 . . |

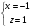 ,
,


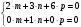 ,
,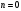 , пусть
, пусть  , тогда
, тогда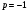 .
. .
.  ,
,  ,
,  ,
, 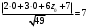
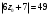


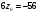 - не подходит, по условию
- не подходит, по условию  .
.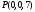 , тогда параметрические уравнения прямой имеют вид:
, тогда параметрические уравнения прямой имеют вид: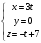
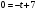 и
и 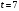 ,
, 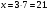

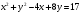

 ,
, .
.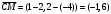 , который можно принять в качестве вектора нормали касательной, составляем уравнение прямой:
, который можно принять в качестве вектора нормали касательной, составляем уравнение прямой: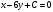 ,
,  принадлежит прямой, значит:
принадлежит прямой, значит: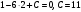

 Докажите, что эта кривая — эллипс. Найдите координаты центра его симметрии. Найдите его большую и малую полуоси. Запишите уравнение фокальной оси. Постройте данную кривую.
Докажите, что эта кривая — эллипс. Найдите координаты центра его симметрии. Найдите его большую и малую полуоси. Запишите уравнение фокальной оси. Постройте данную кривую.

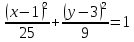

 . Это означает, что большая полуось параллельна оси OX. Следовательно, необходимо только лишь выполнить параллельный перенос начала координат.
. Это означает, что большая полуось параллельна оси OX. Следовательно, необходимо только лишь выполнить параллельный перенос начала координат.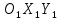 следующим образом:
следующим образом: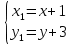

 , её координаты найдем из системы, подставляя значения
, её координаты найдем из системы, подставляя значения 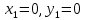 в формулы преобразования координат:
в формулы преобразования координат: 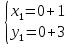
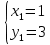

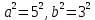 , то большая полуось эллипса
, то большая полуось эллипса 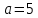 , малая полуось эллипса
, малая полуось эллипса  . Фокальная ось эллипса:
. Фокальная ось эллипса: 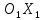 , её уравнение
, её уравнение  , а в старой системе координат
, а в старой системе координат 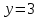 .
.

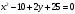 . Докажите, что данная кривая — парабола. Найдите координаты её вершины. Найдите значение её параметра p. Запишите уравнение её оси симметрии. Постройте данную параболу.
. Докажите, что данная кривая — парабола. Найдите координаты её вершины. Найдите значение её параметра p. Запишите уравнение её оси симметрии. Постройте данную параболу.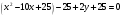

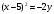 ,
, 