Решение Формула является тождественно истинной. Вариант 24 кр4
 Скачать 248 Kb.
|
Контрольное задание 3 (вариант 2) Доказать тождественную истинность  Решение  Формула является тождественно истинной. Вариант 24 КР4 Записать формулу функции f(x1;x2;x3) и минимизировать ее графическим методом, методом Карно, Квайна, Мак-Класки, Вейча
Решение СДНФ:  Графический метод 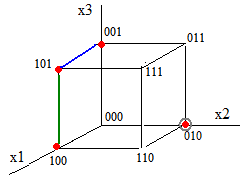 Минимальная ДНФ:  Методом Карно (коэффициентов)
Минимальная ДНФ:  Методом Квайна
Сокращенная ДНФ:  Таблица покрытия
Минимальная ДНФ: Методом Квайна Мак-Класки
Таблица покрытия
Минимальное покрытие: 010 v -01 v 10- Минимальная ДНФ: Метод Вейча  Минимальная ДНФ: КР5 Следующие высказывания записать в виде формул логики предикатов: «Студенты, которые пишут конспекты, не пишут шпаргалки » Пусть х  {люди}, у {вещи, которые можно читать и писать}. На этих областях определения заданы предикаты: S(x):x – студент, R(x,y): x пишет y, K(y): y-конспект Н(у): y-шпаргалка Решение  Построить таблицы истинности на области интерпретации D ={1,2}. x(y(P(x) →(RQ(y)))) Предикаты P(x), Q(y) на области интерпретации D={1,2} принимают следующие значения: 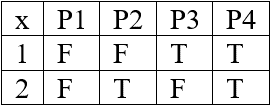 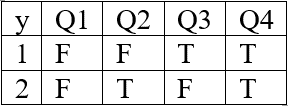 Решение Е = x(y(P(x) →(RQ(y)))) Поскольку предикат P(x) принимает 4 значения, предикат Q(y) принимает 4 значения, и в формуле Е нет свободных переменных, ее таблица истинности будет состоять из 4·4=16 строк. При |R|=F: Е = x(y(P(x) →(FQ(y)))) =x(y(P(x) →(  Q(y)))) ==x(y( P(x)  Q(y))) =xy( P(x) Q(y))Пример расчета на интерпретации (P1,Q1): 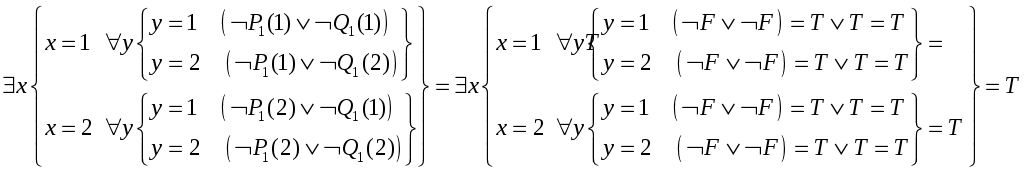 Аналогично получаем значения формулы Е на всех интерпретациях при |R|=F
При |R|=T: Е = x(y(P(x) →(TQ(y)))) =x(y(P(x) →(Q(y)))) = =x(y( P(x) Q(y))) =xy( P(x) Q(y))Получаем значения формулы Е на всех интерпретациях при |R|=F
|
*
*
(1 и 4) 
(3 и 4) 
*