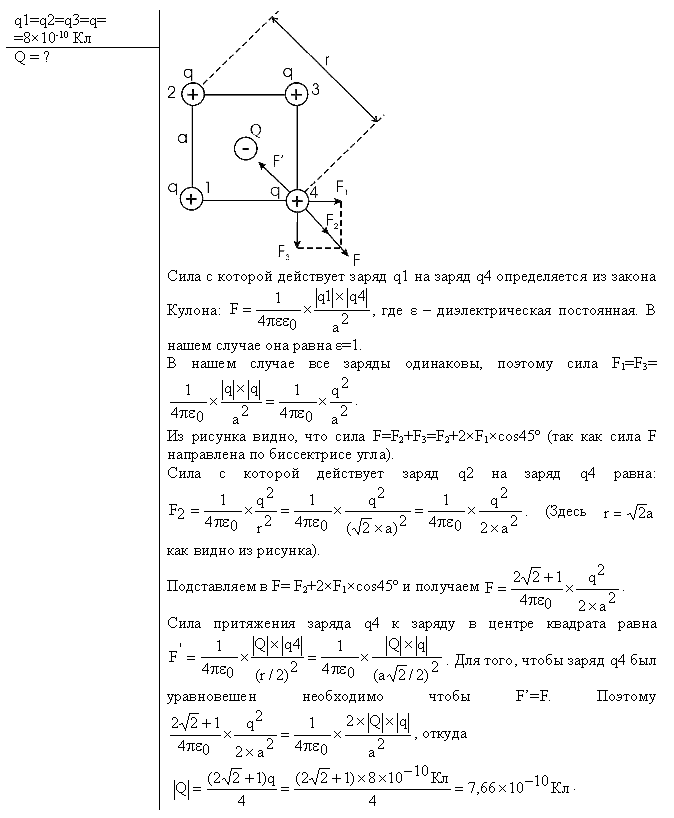
ЗАДАЧИ ПО ФИЗИКЕ. Задачи физика готовые. Решение g 9, 8 н кг t 19. 6 8221 c
 Скачать 1.11 Mb. Скачать 1.11 Mb.
|
-18.086 КДжЗадачи Два тела брошены вертикально вверх из одной точки с интервалом времени 2 сек. с одинаковой скоростью 19,6 м / с. Через какое время тела столкнутся? Решение: g=9,8 Н/кг t= 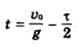 = 19.6/9.8-2/2=1 c. = 19.6/9.8-2/2=1 c.h = Ответ. 14,7 м. Начальная скорость брошенного камня равна v0 = 10 м / с. а спустя t=0,5 с скорость камня равна V =7 м/с. На какую высоту над начальным уровнем поднимается камень? v0=10 м/с v=7 м/с t=0.5 с Решение: Максимальная высота подъема тела, брошенного под углом к горизонту, может быть найдена из общей формулы пути при равнопеременном движении в проекции на вертикальную ось 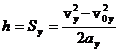 с учетом, что в наивысшей точке траектории отсутствует вертикальная составляющая скорости vy=0, а Неизвестную проекцию начальной скорости на вертикальную ось v0y можно найти из формулы скорости при равнопеременном движении и теоремы Пифагора для полной скорости в начальный момент времени и спустя время t после начала движения: Здесь учтено, что проекция скорости на горизонтальную ось Из (5) находим v0y: Далее из (1) находим высоту подъема: Ответ: h=2.99 м 3.Две гири массой 3 кг н 5 кг висят на концах нити, перекинутой через невесомый блок, причем в начальный момент легкая гиря находилась на 2 м ниже тяжелой. Определить время, через которое гири окажутся на одной высоте. Решение: 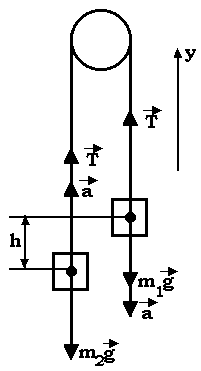 Второй закон Ньютона для первой гири где равнодействующая сила Проекции на ось У У: Выразим силу натяжения нити Второй закон Ньютона для второй гири где равнодействующая сила Проекции на ось У У: Подставим выражение для силы натяжения нити и найдем ускорение системы а= 9,8* 5-3/3+5=2,45 м/с2 Гири окажутся на одинаковой высоте, когда пройдут путь h1=h2=2/2=1 м Перемещение гири за время t Время перемещения t= Ответ: t=0,9 с. 4. Расстояние между центрами Земли н Солнца равно 15* 107 км Земля обращается вокруг Солнца со скоростью приблизительно 30 км/с. Как велика масса Солнца? Решение: М= где 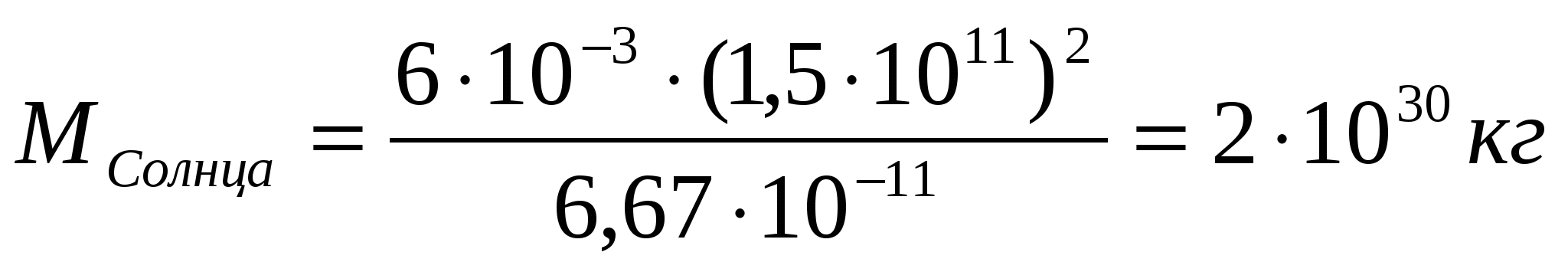 Ответ. 2*1030 кг. 5 Какую скорость приобретает шарик, скатившись с наклонной плоскости и высотой 0.5 м (учесть момент инерции шарика)? Решение: 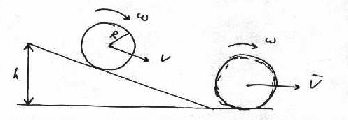  = Ответ. 2,64 м/с. 6.Граната, летящая со скоростью 10 м/с, разорвалась на дна осколка. Больший осколок, вес которого составляет 60% веса всей гранаты. продолжал двигаться в прежнем направлении, но с увеличенной скоростью, равной 26 м/с. Найти скорость меньшего осколка. Решение: 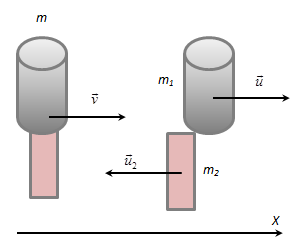 Закон сохранения импульса (ЗСИ): импульс системы остается постоянным при любых взаимодействиях внутри системы, или импульс системы граната до взрыва равен импульсу этой системы после взрыва граната: Проекция на ось x: Скорость второго осколка U2 = 0,6m*26-m10*/0.4m= 14 м/с Ответ: 14 м/с. 7. Найти число молекул азота в 1 см3при нормальных условиях и обладающих скоростью: а) между 99 м/с и 101 м/с; б) между 499 м/с и 501 м/с. Решение: 1)норм условия: po=105 Па; V=1см3=10-3м3 Mr(N2)=28 v1=99м/с v2=101м/с уравнение клаузиуса po=nmo(v2)/3 n=N/V - концентрация вещ-ва масса молеулы азота mo=1aem*Mr(N2)= 1.66*10- 27*28=46.48*10-27 кг средняя квадратичная скорость v2=(v12+v22)/2=(992+1012)/2=10001 тогда po=Nmo(v2)/3V N=3poV/mo(v2)=3*105*10-3/46.48*10-27*10001=645*1020 молекул 2) норм условия: po=105 Па; V=1см3=10-3м3 Mr(N2)=28 v1=499м/с v2=501м/с уравнение клаузиуса po=nmo (v2)/3 n=N/V - концентрация вещ-ва масса молеулы азота mo=1aem*Mr(N2)= 1.66*10- 27*28=46.48*10-27 кг средняя квадратичная скорость v2=(v12+v22)/2=(4992+5012)/2=250001 тогда po=Nmo(v2)/3V N=3poV/mo (v2) =3*105*10-3/46.48*10-27*250001=258*1020 молекул Ответ: 645*1020; 258*1020 8. Определить молярные теплоемкости газа, если его удельные теплоемкости Сv= 10,4 кДж/(кг*К) и Ср= 14,6 кДж/(кг*К) Решение:  Ответ: 29,2 Дж/мольК; 20,8 Дж/мольК. 9.Объем водорода при изотермическом расширении увеличился в n= 3 раза. Определите работу А. совершенную газом и теплоту, полученную при этом. Масса m водорода равна 200 г. Решение:  Ответ. 0,274 МДж. 10. Водород массой m=40г, имевший температуру T=300К, адиабатически расширяется увеличив объем в n1=3раза. Затем при изотермическом сжатии объем газа уменьшился в n2=2раза. Определить полную работу А, совершенную газом, и конечную температуру Т газа. Решение: Температуры и объемы газа, совершающего адиабатный процесс, связаны между соотношением Т2/Т1 = 1/n1^y-1 n1= V2/V1 где y – отношение значений теплоемкости газа при постоянном давлении и постоянном объеме; Отсюда получаем следующее выражение для конечной температуры: T2=T1/n1^y-1 Работа А1 газа при адиабатном расширении может быть определена по формуле A1=m*i/2M*R(T1-T2) Работа А2 газа при изотермическом процессе может быть выражена в виде A2=m/M*R*T2*ln(1/n2) n2= V2/V3 Произведем вычисления с учетом, что для водорода как двухатомного газа y=1,4, i=2 и М=2·10-3 кг/моль: T2=300/2^0.4= |

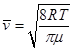 (13)
(13)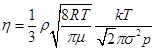 (14)
(14)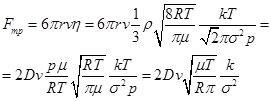 (15)
(15)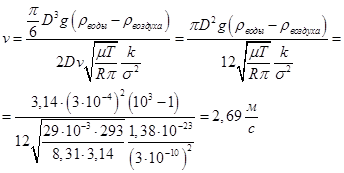
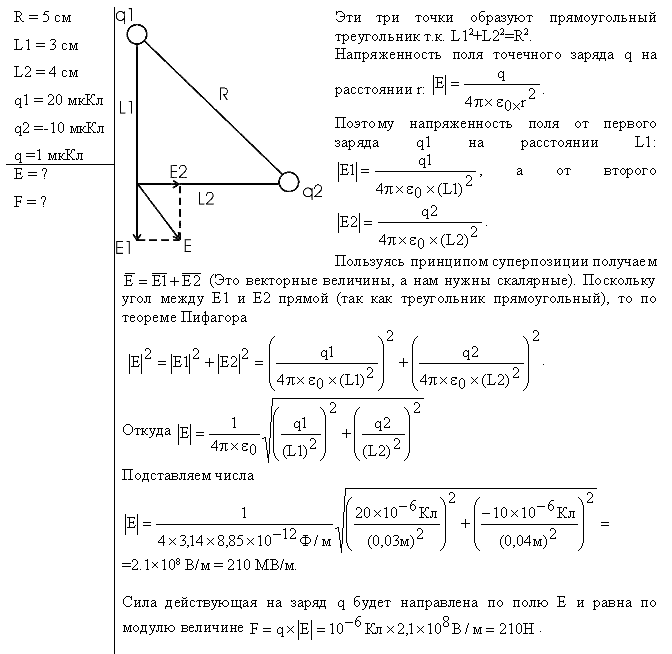 Ответ. 210 Н.
Ответ. 210 Н.