Методмческие указания по выполнению КР№1. Решение инженерногеодезических задач на топографических картах и планах для студентов, обучающихся по направлению 653500 Строительство
 Скачать 28.66 Mb. Скачать 28.66 Mb.
|
|
Масштабные условные знаки применяют для заполнения контуров природных, сельскохозяйственных угодий. Они состоят из знака границы угодий, - точечный пунктир или тонкая сплошная линия и заполняющих его изображений или условной окраской. Внемасштабные условные знаки служат для изображения объектов, размеры которых не изображаются в масштабе карты (мосты, километровые столбы, колодцы, геодезические пункты, квартальные столбы и т.д.) Они, как правило, определяют местоположения объектов, но по ним нельзя судить об их размерах. Линейные условные знаки показывают объекты, протяженность которых значительно больше их ширины (дороги, реки, линии связи и электропередач, просеки в лесу и т.д.) Их длина выражается в данном масштабе. У этих знаков приводятся различные характеристики в метрах: ширина проезжей части и всей дороги, высота насыпи и глубина выемки, материал покрытия и т.д. Пояснительные условные знаки представляют собой подписи, дающие характеристики и названия объектов, например, глубина и скорость течения рек, грузоподъемность и ширину мостов, названия пород деревьев и т.д. Специальные условные знаки устанавливают соответствующие ведомства отраслей народного хозяйства. Их применяют для составления специальных карт и планов этой для отрасли (лесоустроительных, землеустроительных, дорожной сети, геологических и т.д.). Условные знаки дают ясное и наглядное представление о местности. Хорошие знания их позволяет легко представить изображаемую на карте местность. Задача 3.1. Изучить условные знаки топографических планов масштабов 1:1000 и 1:500 по книге[4]. Вычертить условные знаки, номера которых оканчиваются на Ваш номер в журнале преподавателя[4] .Сделать описание местности, изображенной на ксерокопии Вашей топографической карты. 4.Система плоских прямоугольных координат Гаусса-Крюгера При картографировании значительных частей земной поверхности с целью перехода от сферы к плоскости применяют различные картографические проекции. Дело в том, что сферическую поверхность развернуть в плоскость без разрывов невозможно. Поэтому любая картографическая проекция имеет искажения. Их величина зависит от вида проекции. Так в равноугольных проекциях сохраняется подобие углов, но искажаются длины линий; в равновеликих не искажаются площади, в равнопромежуточных – не искажаются длины линий по какому-либо направлению (по меридиану, параллели) и т.д. Для целей крупномасштабного картографирования, то есть для составления топографических карт, применяют равноугольную поперечно-цилиндрическую проекцию Гаусса-Крюгера. В этой проекции сохраняются подобие изображения фигур при переходе с эллипсоида на плоскость, а искажение длин линий не выходит за пределы графической точности. Геометрический смысл этой проекции заключается в следующем. Поверхность сферы разбивают меридианами через 6 градусов на зоны, каждая из которых отдельно проецируется на боковую поверхность цилиндра (рис 9). Разрезав цилиндр по образующей, проходящей через земные полюса, получают изображение сферической поверхности на плоскости (рис 10). На полученном изображении осевой меридиан зоны (меридиан касания зоны и цилиндра) и экватор ,- взаимно перпендикулярные прямые линии, а остальные меридианы и параллели – кривые. Искажения размеров длин линий в близи осевого меридиана минимальные и возрастают по мере удаления к краям. Линия на поверхности шара длиной D при изображении ее на плоскости получит искажение ∆D, которое можно вычислить по формуле: ∆D=Y²mD/2R², (3) где Ym=(Y1+Y2)/2 – среднее значение из ординат начальной и конечной точек линии; R – радиус Земли. 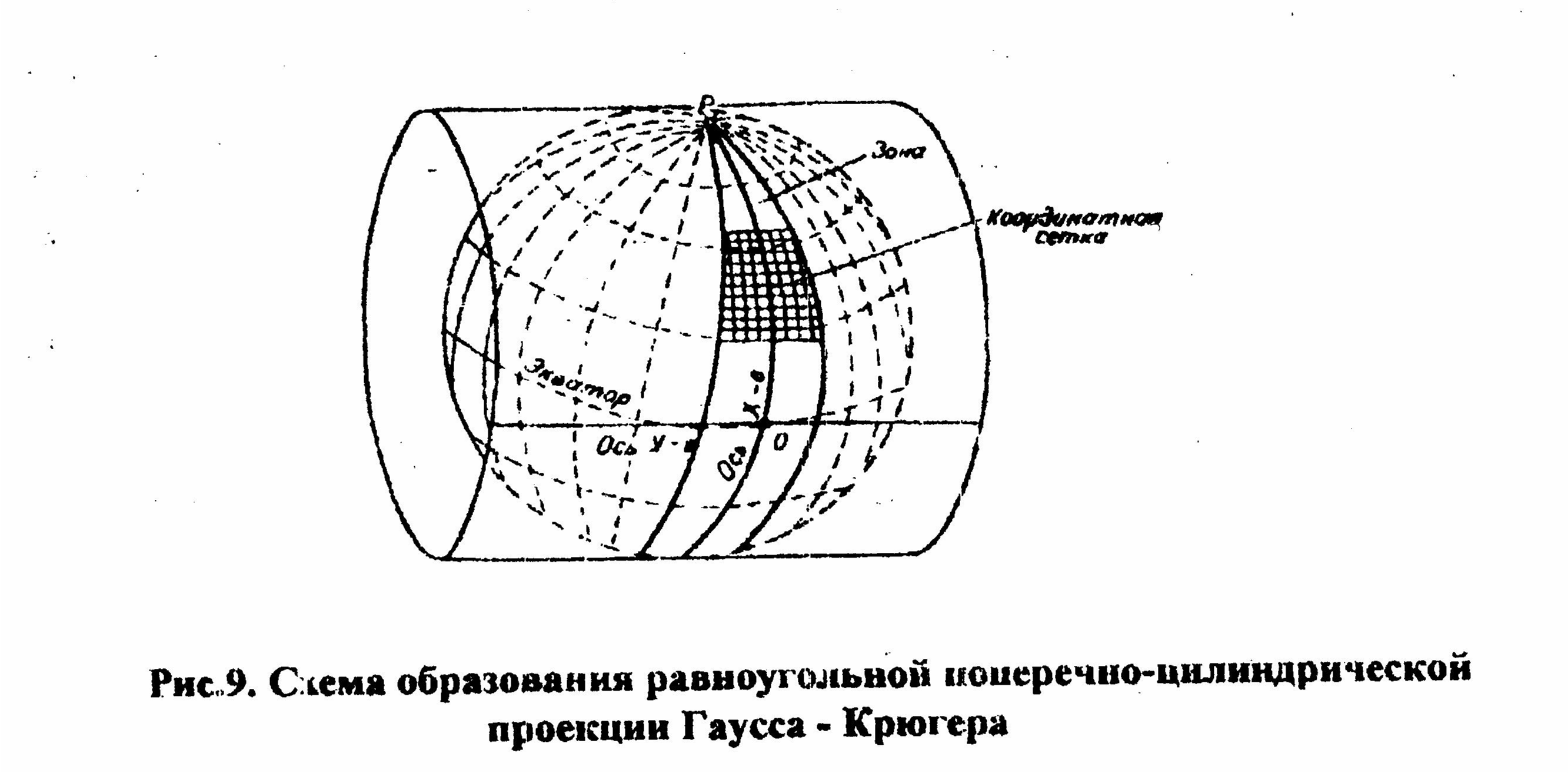 Рис.9. Схема образования равноугольной поперечно – цилиндрической проекции Гаусса – Крюгера Относительные искажения ∆D/D на краях шестиградусной зоны могут достигать величины порядка 1/1500, а трехградусной – 1/6000. Выбор ширины зоны зависит от требований, предъявляемых к точности топографической карты. Если для проектирования нужны карты масштаба 1:10 000 и мельче, то применяют шестиградусные зоны, для более крупных масштабов – трехградусные. В каждой зоне, а их 60, задаётся своя система прямоугольных координат, в которой за ось абсцисс (Х) принимается осевой меридиан, а за ось ординат (Y) – экватор (рис 10). 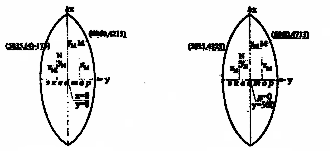 а) непреобразованная б)преобразованная Рис. 10. Система плоских прямоугольных координат Гаусса – Крюгера Зоны нумеруются арабскими цифрами с запада на восток, начиная от Гринвичского меридиана. Для удобства измерения прямоугольных координат на карте проводят сетку, состоящую из прямых линий, параллельных осевому меридиану и экватору, которая называется координатной. Расстояние между смежными линиями сетки для масштабов карт 1:10 000, 1:25 000, 1:50 000 составляет 1 км на местности. У западной и восточной рамок карты подписывают абсциссы, а у северной и южной - ординаты координатной сетки. Они позволяют легко определить прямоугольные координаты любой точки, изображенной на карте. Для территории нашей страны расположенной в северном полушарии, абсциссы всегда положительны и их величина соответствует расстоянию от экватора до данной линии. Для того, чтобы и ординаты были всегда положительными, их начало смещают на запад на 500 км. Задача 4.1. определить прямоугольные координаты вершин треугольника. Для решения задачи каждому студенту необходимо иметь ксерокопию карты, на которой преподаватель наносит вершины треугольника АВС. Прежде чем приступить к решению задачи необходимо определить масштаб карты и разобраться с оцифровкой сетки координат. Затем выделить квадрат километровой сетки, в которой находится вершина треугольника и выписать координаты его юго-западного угла. На рис. 11 для точки А Х=6068 км, Y=4312 км ( напоминаем, что первая цифра у ординаты означает номер зоны, в которой находится данная карта). 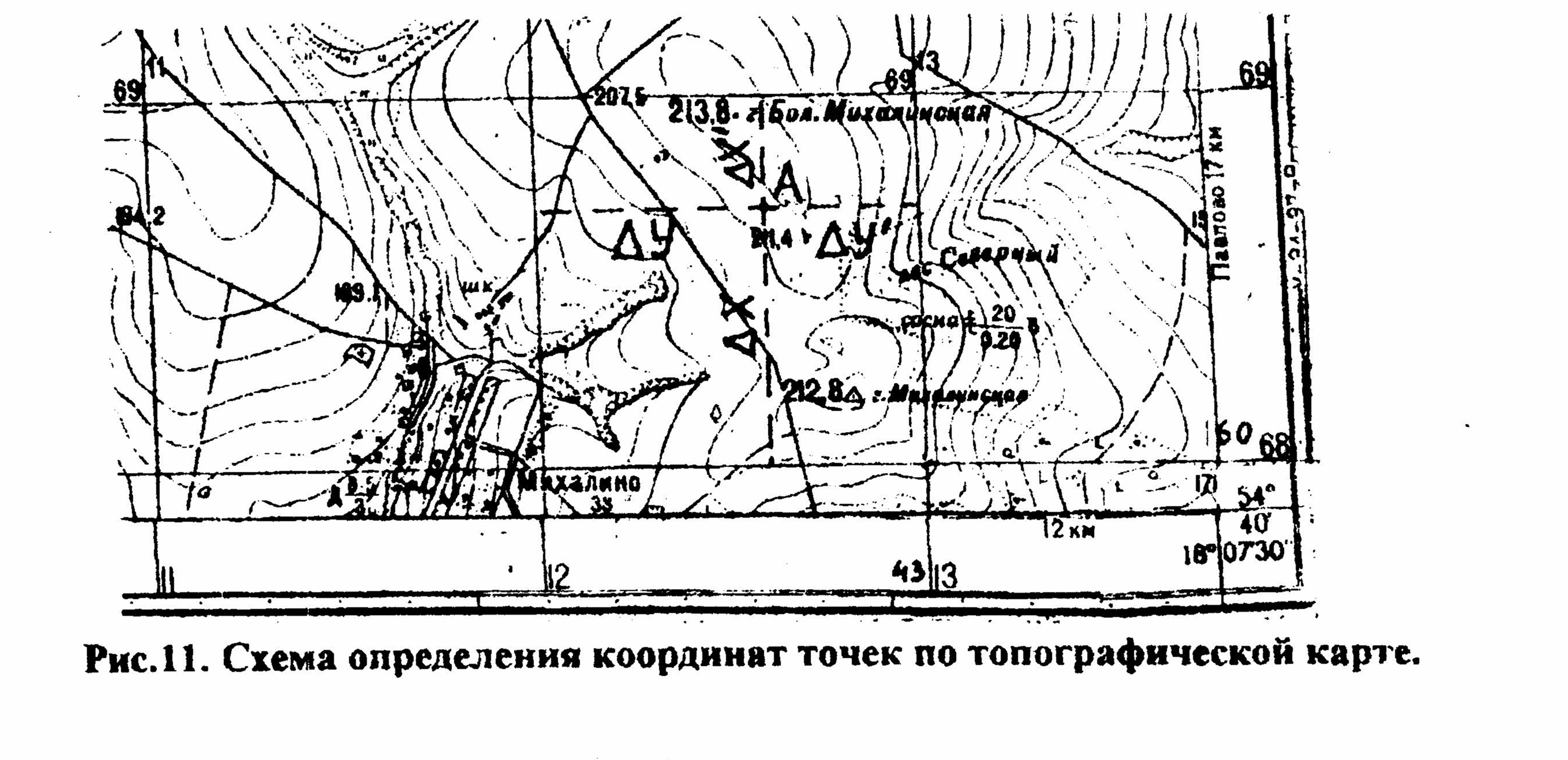 Рис. 11. Схема определения прямоугольных координат на топографической карте Из точки А опускают перпендикуляры на стороны квадрата километровой сетки. С помощью измерителя и масштабной линейки определяют длины перпендикуляров относительно южной и западной стороны квадрата. То есть измеряют приращения координат. Тогда значения координат точки А будут равны: XA=Xю.з.+ ∆XA (4) YA=Yю.з..+ ∆YA (5) Недостатком изложенного способа является его бесконтрольность. Здесь любая грубая ошибка в измерении остается незамеченной. Поэтому на практике измеряют не только отрезки ∆ХА и ∆YA, но и продолжения их до северной и восточной сторон километровой сетки, т.е., ∆ХА´ и ∆YA´. Очевидно, что при отсутствии погрешностей в измерениях должны выполнятся условия: ∆XA +∆ХА´=D (6) ∆YA+∆YA´=D, (7) где D – длина стороны квадрата километровой сетки (1км). Практически таких равенств не получается из-за случайных и систематических погрешностей измерений (деформация бумаги, не точность установки игл измерителей в вершины, погрешности построения поперечного масштаба и т.д.). Однако величина неравенства не должна превышать 0.3мм в масштабе карты. Если это условие выполняется, то окончательные координаты точки А можно вычислить по формулам. XA=Xю.з+(D/(∆XA +∆ХА´))∆XA, (8) YA=Yю.з+(D/(∆YA +∆YB´))∆YA. (9). Данные формулы и рекомендуется использовать при решении задачи 4.1. результаты измерений записывают в таблицы 2 и 3. Однако такой контроль не всегда осуществим. Например, в таблице 2 отрезок ∆ХА´ отсутствует, так как линия координатной сетки 6069 находится на соседнем листе карты. В таких случаях наиболее действенным контролем является вычисление длины отрезка dAB и сравнение его с непосредственно измеренной длиной этого отрезка по карте. Это поможет избежать грубой погрешности определения координат. В таблицах 2 и 3 приведены результаты измерения координат вершин треугольника АВС ( см. Приложение 1). Таблица2 Абсциссы точек А, В,С. (км)
Таблица 3Ординаты точек А,В,С (км)
Задача 4.2. По измеренным в задаче 4.1 прямоугольным координатам вычислить длины сторон треугольника и сравнить их с непосредственно измеренными. Задача распадается на 2 части. В первой части необходимо вычислить длины сторон по известной в математике формуле dAB=√(XA-XB)²+(YA-YB)², (10) вычисленные расстояния записать в таблицу 4 с числом значащих цифр, соответствующих точности масштаба карты. Вторая часть задачи состоит в непосредственном измерении длин сторон треугольника с помощью измерителя и построенного в задаче 1.1 поперечного масштаба. Результаты измерений также записать в таблицу 4. Найти расхождения между вычисленными и измеренными длинами сторон треугольника и дать анализ их соответствия точности масштаба карты. Перечислить причины возникновения этих расхождений. Таблица 4. Значения длин сторон треугольника, полученные при вычислениях и измерениях.
Вопросы для самоконтроля.
Ориентировать линию или карту – значит определить ее расположение относительно географического (истинного), осевого или магнитного меридианов. В зависимости от этого углы ориентирования носят названия: истинный азимут; дирекционный угол; магнитный азимут. Угол ориентирования, отсчитываемый от северного направления географического меридиана по ходу часовой стрелки, называется истинным азимутом. Так как географические меридианы не параллельны между собой, то значения истинных азимутов прямого от обратного отличаются не на 180 градусов, а плюс ещё сближение меридианов, величина которого зависит от разности долгот меридианов и широты в точке измерения. Если угол ориентирования измеряется относительно северного направления осевого меридиана, то его называют дирекционным углом. А если угол ориентирования измеряется относительно северного направления магнитного меридиана, то его называют магнитным азимутом. Каждый из названных углов ориентирования может принимать значения от нуля до 360 градусов. Кроме названных основных углов ориентирования на практике находят широкое применение их производные значения, - румбы. Румб это всегда острый угол, измеряемый от ближайшего направления меридиана (истинного, осевого или магнитного). В строительной практике чаще всего ориентирование выполняют относительно осевого меридиана. Целью решения предлагаемых ниже задач на ориентирование является приобретение навыков измерения углов ориентирования на картах и топографических планах, а также понимание связи между ними с целью возможности перехода от одного угла к другому. Задача 5.1. Измерить с помощью транспортира истинные азимуты линий АВ, ВС, СА, ВА, СВ, АС. Вычислить румбы и внутренние углы треугольника АВС. Горизонтальный угол составленный северным направлением географического (истинного) меридиана и заданной линией, измеренный по ходу часовой стрелки, называется истинным азимутом. Согласно определения для измерения азимута линии АВ необходимо провести географический меридиан, пересекающий сторону АВ треугольника (приложение 1) или продолжить сторону АВ до пересечения с меридианом, ограничивающим лист карты с запада или востока. От северного направления этого меридиана по ходу часовой стрелки транспортиром измерить искомый угол ориентирования. Результат измерения занести в таблицу 5. Точно также измерить азимуты остальных сторон. От азимутов перейти к истинным румбам и вычислить величины внутренних углов треугольника, используя правило: угол равен разности правого и левого направлений. Если измерения не содержат грубых погрешностей, то расхождения между значениями прямых и обратных азимутов должно быть 180°. Сумма внутренних углов треугольника должна быть равна 180°. Отклонения от этих величин не должны превышать тройной точности транспортира. В качестве примера в таблице 5 приведены значения азимутов сторон треугольника АВС (приложение 1). Таблица 5 Результаты измерений истинных азимутов сторон треугольника АВС
В практике, кроме непосредственно измеренных углов ориентирования, часто используют их производные – румбы (рис.13). Истинным румбом линии называется угол между ближайшим (северным или южным) направлением истинного меридиана и заданной линией. Чтобы различить, какое направление относительно сторон горизонта имеет данная линия, перед градусной величиной румба указывают название соответствующей четверти. Например: СВ: 45°00´, ЮЗ: 15°00´ и т.д. Для перехода от азимутов к румбам необходимо использовать рис.13 или табл. 6. 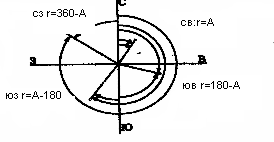 Рис.13. Связь между истинными румбами и азимутами Что касается вычисления внутренних углов треугольника, то необходимо пользоваться следующим правилом: внутренний угол треугольника равен разности азимутов правой и левой стороны треугольника, если мысленно встать в вершину вычисляемого угла лицом в сторону искомого угла. Например, угол А равен разности азимутов линий АС и АВ, т.е. 186030´ - 128000´ = 58030´. Таблица 6.Связь между румбами и истинными азимутами
Задача 5.2. Измерить с помощью транспортира прямые и обратные дирекционные углы линий АВ,ВС,СА. Вычислить значения их румбов и внутренних углов треугольника. Как уже отмечалось, одним из существенных недостатков истинных азимутов и румбов, как углов ориентирования, является их зависимость от широты точки, в которой измеряется угол, а также неравенство прямого и обратного угла. Поэтому на практике более широкое распространение получили углы ориентирования, называемые дирекционными углами α Угол, отсчитываемый от северного направления осевого меридиана или линии параллельной ему по ходу часовой стрелки до направления данной линии, называется дирекционным углом. Прямой и обратный дирекционные углы отличаются ровно на 180° Дирекционные углы отличаются от азимутов на величину гауссова сближения меридианов γг . Применительно к проекции Гаусса – Крюгера формула вычисления γг имеет вид γг= (L-L0)sinB, (12) где L – долгота меридиана в определяемой точке, L0 – долгота осевого меридиана данной зоны. Номер зоны всегда подписан первой цифрой перед значением координаты Y. Например, для зоны с номером 4, долгота осевого меридиана равна 210. Гауссово сближение меридианов может быть восточным или западным в зависимости от положения точки относительно осевого меридиана. Для восточной половины зоны сближение меридианов считается положительным, для западной – отрицательным. На топографической карте ниже южной рамки всегда указывается гауссово сближение меридианов для средней части листа. В практике, кроме непосредственно измеренных углов ориентирования, часто используют их производные – румбы (рис.13). Дирекционным румбом линии называется угол между ближайшим (северным или южным) направлением осевого меридиана и заданной линией. Чтобы различить, какое направление относительно сторон горизонта имеет данная линия, перед градусной величиной румба указывают название соответствующей четверти. Например: СВ: 45°00´, ЮЗ: 15°00´ и т.д.  Рис.13. Связь между дирекционными углами и румбами Используя связь между румбами и основными углами ориентирования по рис.13 или таблице 6 легко перейти от дирекционных углов к их румбам и наоборот. Таблица 6.Связь между румбами и дирекционными углами
Так как дирекционный угол – это угол между северным направлением осевого меридиана и направлением заданной линии, измеренный по ходу часовой стрелки, то решение первой части задачи сводится к измерению угла между вертикальной линией сетки (осью абсцисс) и заданной линией. Результаты измерений следует записать в табл.8. В качестве примера в ней переведены результаты измерений дирекционных углов сторон треугольника АВС приложения 1. Таблица 8.Результаты измерения дирекционных углов сторон треугольника АВС
Дирекционные углы можно не только непосредственно измерить на карте, но и вычислить по формуле 13, если известны координаты концов отрезка, т.е XА YА XВ YВ. Однако следует иметь в виду что по этой формуле всегда будем иметь румб линии. tg rAB=(YВ-YА)/(XВ-XА). (13) Для перехода от румба к дирекционному углу необходимо установить название четверти, в которой он находится, ориентируясь на знаки приращений координат (YВ-YА) и (XВ-XА) в соответствии с табл.9, а уже затем вычислить искомый дирекционный угол, используя связь между дирекционными углами и их румбами по табл.6 или рис.13. Таблица 9. Знаки приращений координат в зависимости от четверти румба
Задача 5.3. Вычислить дирекционные углы сторон АВ,ВС,СА по формуле 13, используя прямоугольные координаты, полученные в задаче 4.1 и сравнить их с измеренными (табл.8). дать анализ причин расхождений между вычисленными измеренными величинами. Таблица 10.Результаты сравнения вычисленных и измеренных дирекционных углов
Задача 5.4. Найти сближение меридианов как разность между географическим азимутом и дирекционным углом и сравнить его с вычисленным по формуле 12 для точек А,В,С. Дать анализ причин расхождений. γизм и γвыч. (для любознательных) Таблица 11. Вычисление сближений меридианов
Задача 5.5. Вычислить магнитные азимуты линий АВ,ВС,СА, используя значения дирекционных углов (табл.8), а склонение магнитной стрелки и сближение меридианов взять из приложения 2 по заданному преподавателем варианту. Решение задачи иллюстрировать рисунками. (для любознательных) Ориентирование линий относительно магнитного меридиана является наиболее простым в практическом исполнении, так как положение магнитного меридиана на местности даёт направление магнитной стрелки. Но такого рода ориентирование не находит широкого применения в массовых геодезических работах и особенно на строительной площадке. Это обусловлено изменением величины склонения магнитной стрелки в зависимости от места и времени. Так, на Европейской части России, восточное склонение колеблется от 0° (в районе Калининграда) до 20° (в районе Нарьян-Мара). С 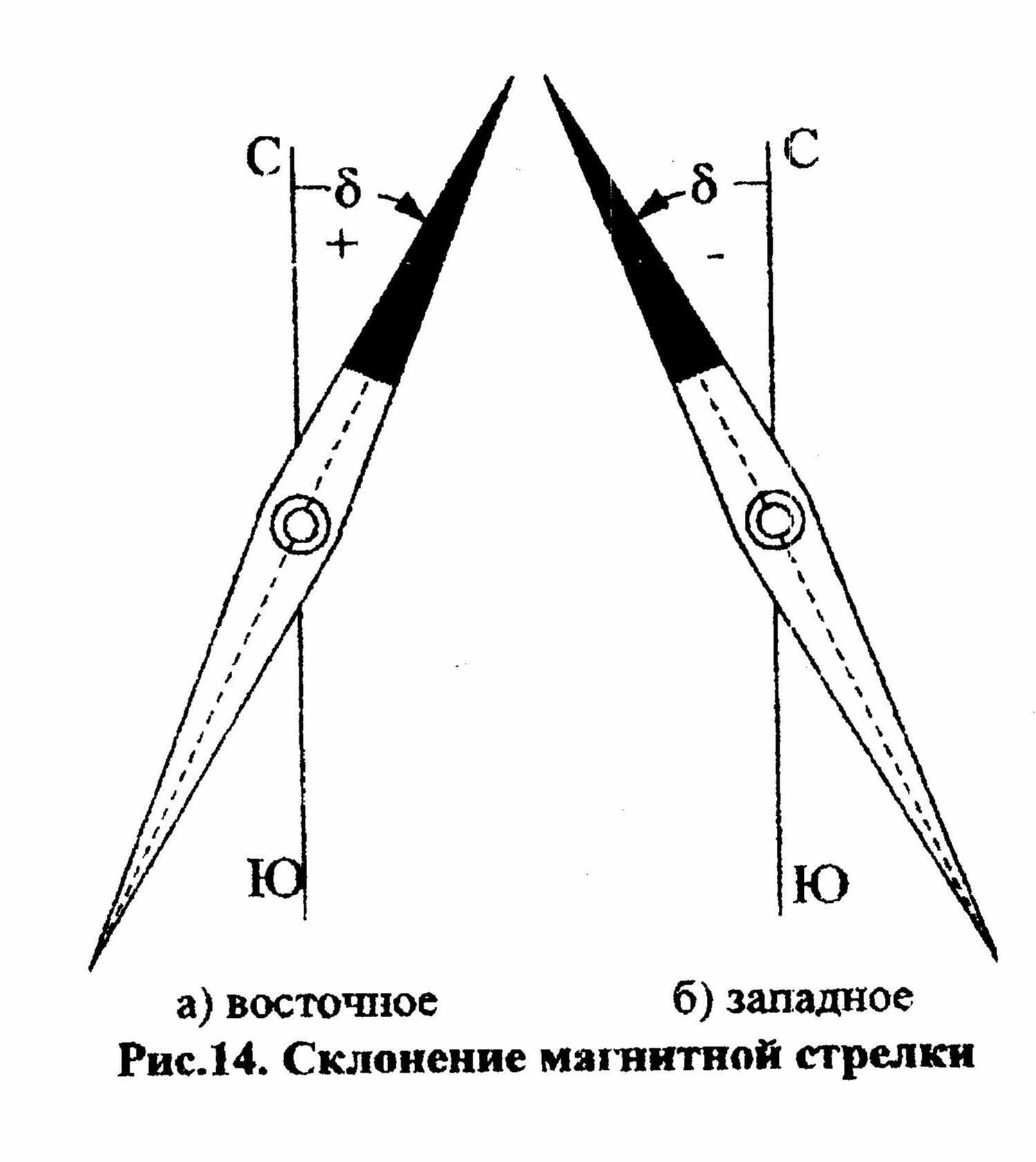 клонение магнитной стрелки есть угол между северными направлениями истинного и магнитного меридиана (рис.14). клонение магнитной стрелки есть угол между северными направлениями истинного и магнитного меридиана (рис.14). Cклонение магнитной стрелки может быть восточным и западным. Восточному склонению приписывают знак (+), а западному (-). Это обусловлено положением магнитного меридиана относительно географического (истинного). Склонение претерпевает вековые, годовые и суточные изменения. Вековые изменения склонения продолжительностью около четырех веков имеют амплитуду в несколько десятков градусов. Амплитуда годовых колебаний в Европейской части России в отдельных местах достигает 5°, а суточная - 15´. При этом изменение не имеют математически выраженных закономерностей, поэтому учет их представляет определенные трудности. Кроме того, величина склонения изменяет свое значение под влиянием магнитных возмущений и магнитных бурь, связанных с полярным сиянием, солнечной активностью. В районах магнитной аномалии, а также вблизи линий электропередач положение магнитного меридиана становится неопределенным. Все отмеченное выше не позволяет нанести на карту линии магнитных меридианов, а следовательно и измерить по карте магнитный азимут. В тоже время ниже южной рамки топографической карты всегда указывается склонение магнитной стрелки (δ) на дату составления карты, а также годовое изменение склонения. Это позволяет вычислить величину склонения на текущее время, а следовательно и значения истинного азимута. Ориентирование по магнитному меридиану находит широкое применение в лесоустроительных работах и при картографировании небольших участков земной поверхности (менее 1км²) в труднодоступных районах. В этих случаях возникает необходимость перехода от измеренных дирекционных углов или истинных азимутов к магнитным азимутам линий. Связь между ними показана на рис.15. 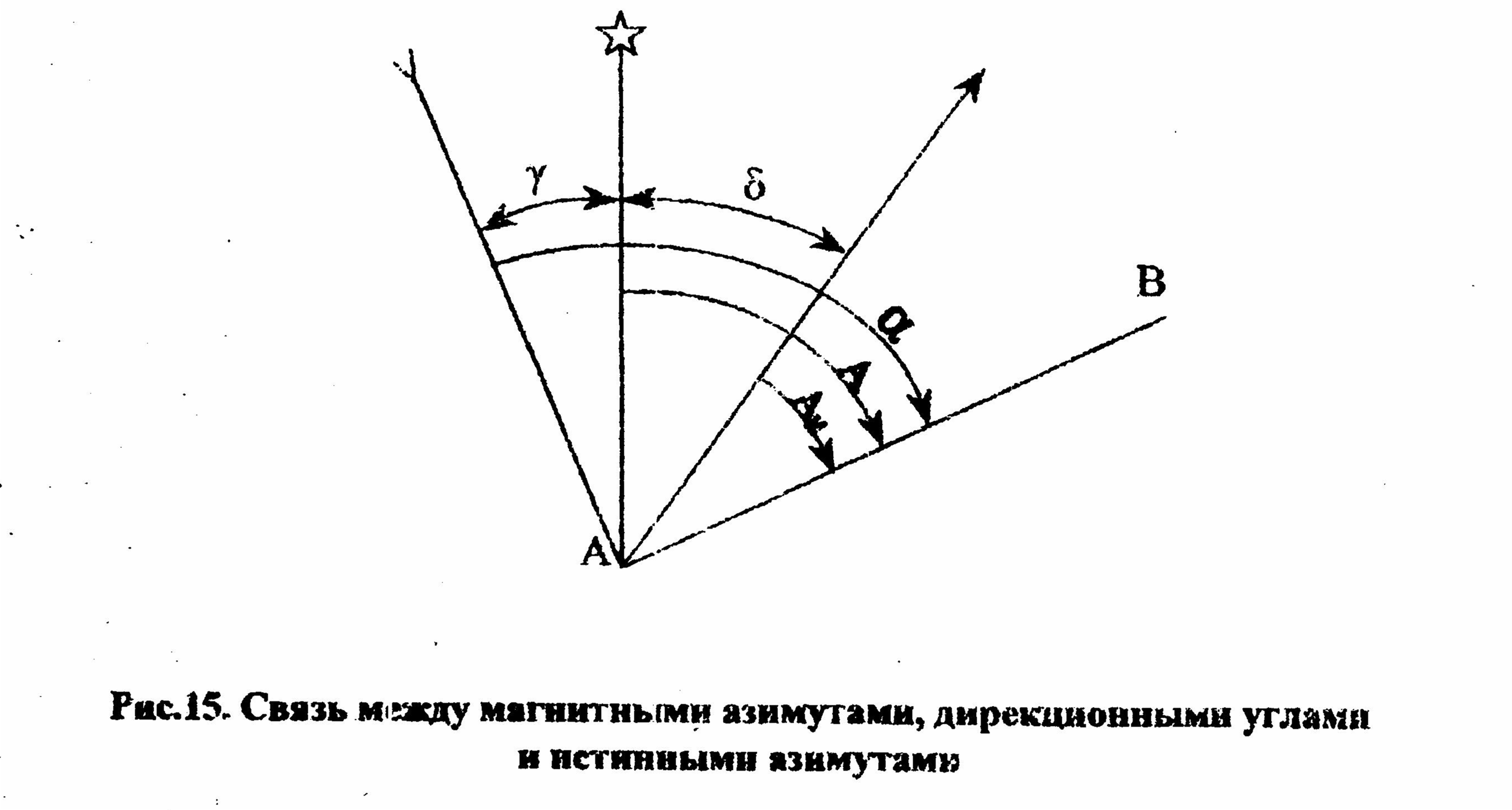 Рис.15 Связь между магнитными азимутами, дирекционными углами и истинными азимутами. На рис 15 линия со звездочкой есть направление истинного (географического) меридиана, а линия с перевернутой стрелкой показывает расположение осевого меридиана относительно географического. Линия со стрелкой показывает расположение магнитного меридиана относительно географического. В данном случае сближение меридианов западное, а склонение магнитной стрелки восточнее. Имея такой чертеж легко перейти от одного угла ориентирования к другому. В табл.12 приведены результаты вычисления магнитных азимутов сторон треугольника при γ=-2°20´западное сближение, и δ=4°15´восточное склонение. Таблица 12. Вычисление магнитных азимутов
Вопросы для самоконтроля.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
