Методмческие указания по выполнению КР№1. Решение инженерногеодезических задач на топографических картах и планах для студентов, обучающихся по направлению 653500 Строительство

• Название: Решение инженерногеодезических задач на топографических картах и планах для студентов, обучающихся по направлению 653500 Строительство
• Анкор: Методмческие указания по выполнению КР№1.doc
• Дата: 08.05.2017
• Размер: 28.66 Mb.
• Имя файла: Методмческие указания по выполнению КР№1.doc
• Тип: Решение; #7291
• страница: 3 из 4

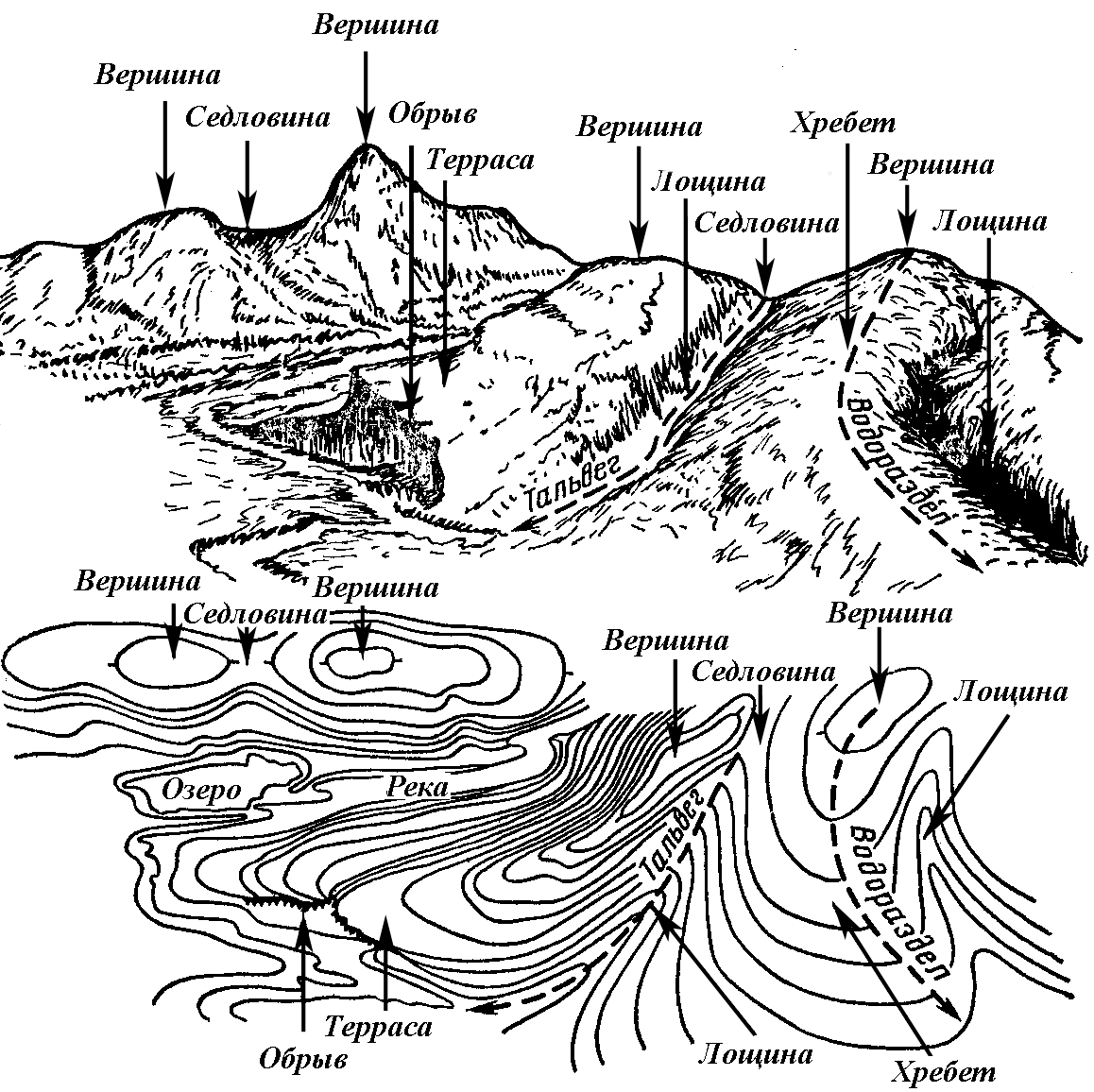
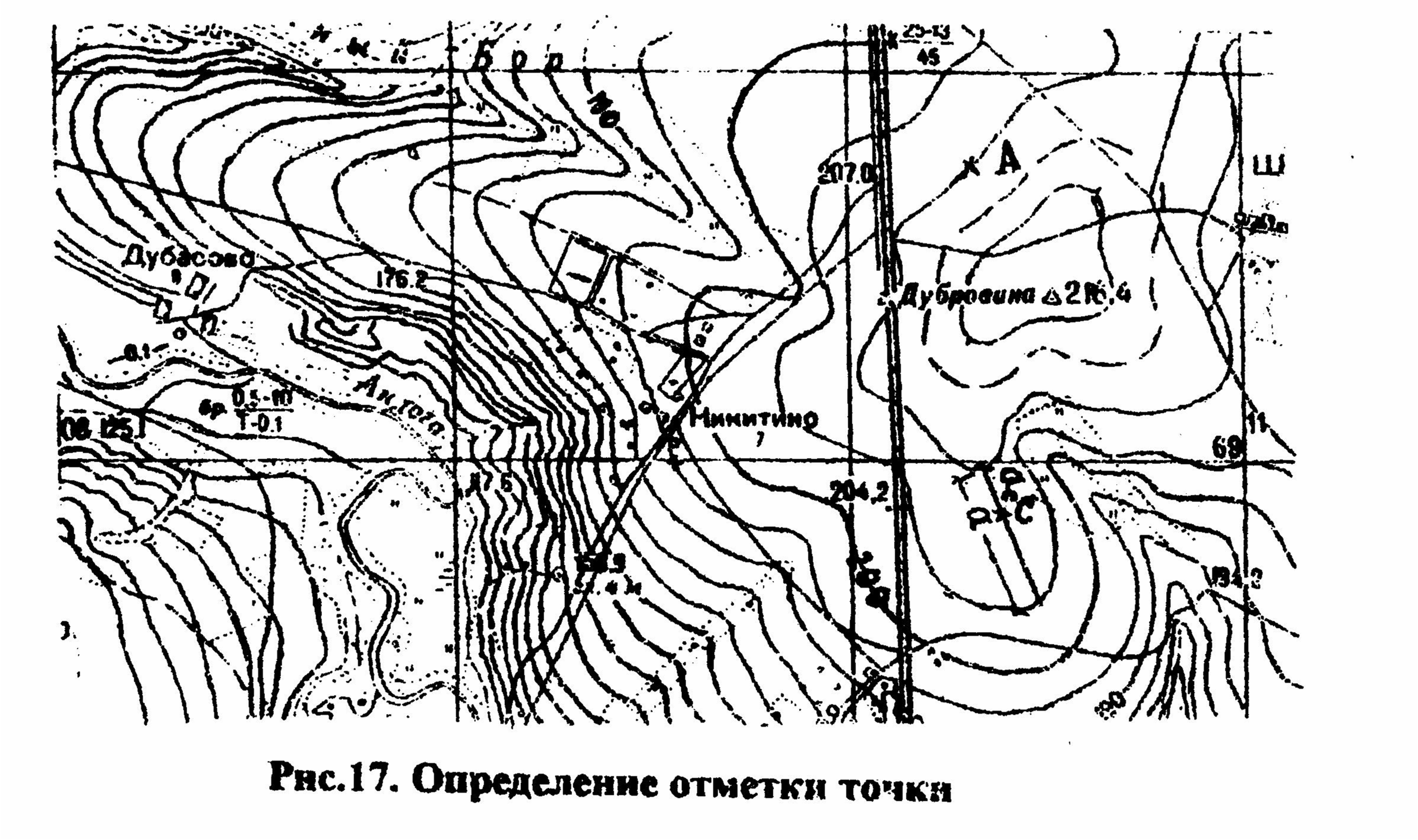
Рельеф местности это совокупность неровностей земной поверхности. Выделяют следующие формы рельефа: гора, котловина, хребет, лощина и седловина (рис.16). На топографических картах и планах рельеф изображается с помощью горизонталей. Горизонталь это плавная кривая, соединяющая точки с одинаковыми высотами. С геометрической точки зрения горизонталь это след от сечения физической поверхности земли горизонтальной плоскостью. Понятие о горизонтали можно получить, если представить себе местность затопленную до заданной высоты непроточной водой. Береговая линия в этом случае и будет являться горизонталью. Изменяя уровень воды, получим горизонтали с различными высотами. На картах и планах высоты горизонталей изменяют через равные промежутки, которые называют высотой сечения рельефа. Таким образом высота сечения рельефа это расстояние по вертикали между смежными секущими плоскостями (рис.17). Она всегда подписана на топографических картах и планах. При необходимости ее можно определить как разность высот соседних горизонталей. Высоту сечения обозначают h_o. Стандартные высоты сечений рельефа топографических карт равны: 2,5 м(1:10000), 5.0 м (1:25000), 10 м (1:50000), 20 м(1:100000). Топографические планы масштаба 1:500 составляют с высотой сечения 0,25 или 0,5 м; 1:1000– 0.5 или 1,0 м; 1:2000 – 1,0 м.

Рис.16. Основные формы рельефа и изображение их горизонталями
Высота сечения зависит от рельефа местности, масштаба и назначения топографического плана. Высота горизонтали всегда кратна высоте сечения рельефа, принятой для составления данной карты (плана). В отдельных случаях, для детализации рельефа, проводят полугоризонтали. Высота сечения в этих случаях равна половине высоты основного сечения рельефа.



Рис. 17. Сечение рельефа горизонтальными плоскостями
Заложение это расстояние на плане между смежными сплошными горизонталями. По заложению можно судить о крутизне ската. Чем меньше заложение, тем круче скат. Заложение обычно обозначают буквой а (рис.17).
На рис 16 представлены основные формы рельефа: гора; котловина: хребет: лощина и седловина.

Гора, холм - конусообразное возвышение. Наивысшая точка – вершина, боковые поверхности – скаты, линия их слияния с окружающей местностью – подошва.

Котловина (впадина) – замкнутое углубление. Самая низкая ее точка - дно. Боковые поверхности – скаты, а линия их слияния с окружающей местностью – бровка.

Хребет – вытянутая и понижающаяся в одном направлении возвышенность. Скаты хребта при пересечении в верхней части образуют линию, которая называется водораздельной.

Лощина – вытянутое и понижающееся в одном направлении углубление. Скаты лощины при пересечении в нижней части образуют линию, которая называется тальвегом (водосливной линией).

Седловина – место слияния двух хребтов смежных гор. Самая низкая точка седловины называется перевалом. От перевала в обе стороны отходят лощины.

Основной характеристикой рельефа является крутизна ската. О ней можно судить по величине заложения. Чем меньше заложение (расстояние между горизонталями), тем круче скат и наоборот. Для проектирования и строительства зданий и сооружений пользуются численными характеристиками крутизны ската, которыми являются уклон i или угол наклона линии ν

i_АВ =(H_B-H_A)/d_AB, (14)

= arc tg(H_B-H_A)/d_AB . (15)

Таким образом для определения крутизны ската достаточно определить по карте высоты концов отрезка и его длину. Уклон линии может быть записан или в виде десятичной дроби (i_АВ = 0.0563), или в процентах (i_АВ = 5.63%), или в промиллях (тысячная доля) (i_АВ= 56.3‰).

Из формул (14) и (15) видно, что уклон линии есть значение тангенса угла наклона

i_АВ = tg ν_АВ, а угол наклона ν_АВ = arctg i_АВ.

При чтении рельефа руководствуются следующими правилами:

1)бергштрихи всегда направлены в сторону понижения;

2)основания цифр, которыми подписаны горизонтали, располагаются в направлении понижения ската;

3) к водоемам и водотокам местность понижается;

4) в одну сторону от горизонтали местность повышается, а в другую понижается;

5) горизонтали перегибаются на водораздельных линиях хребтов и тальвегах лощин;

6) отметка точки, лежащей на горизонтали, равна отметке горизонтали;

7)отметки горизонталей всегда кратны высоте сечения рельефа.

Для отыскания отметки горизонтали находят ближайшую подписанную горизонталь. Отметка искомой будет равна (рис.18).

НА=Н0+nh0 (16)

где Н0 – отметка подписанной горизонтали;

n- число горизонталей между подписанной и искомой горизонталью

h0- высота сечения рельефа.

В формуле знак (+) ставится в случае, если точка А находится выше по склону подписанной горизонтали, а (-) - если ниже. На рис.18 h0=5м, n=2 следовательно НA=210,0м. При отсутствии вблизи определяемой точки подписанной горизонтали, ее отметку находят от ближайшей подписанной отметки характерной точки. В этом случае сначала определяют отметку ближайшей горизонтали. Ее отметка будет кратна высоте сечения рельефа. Например, отметка горизонтали, расположенной ниже вершины горы с Н=216,4 равна 215,0м. От этой горизонтали, руководствуясь описанным выше методом, определяют отметку горизонтали с точкой А.



Рис 18. Определение высоты точки
Если определяемая точка находится между горизонталями, то сначала необходимо определить отметки горизонталей, между которыми они находятся, а затем превышение между горизонталью и определяемой точкой линейным интерполированием

hc=ach0/a, (17)

где hc - превышение между младшей горизонталью с отметкой Н0 и точкой С;

a - заложение

ac - расстояние от младшей горизонтали до точки С.

Тогда отметка искомой точки будет равна

Нс=Н0+ hc (18)

Если определяемая точка лежит между горизонталями с одинаковыми отметками: перевал седловины, вершины горы или дно котловины, то отметка в этих случаях принимается равной отметке ближайшей горизонтали плюс (минус) половина высоты сечения рельефа.

Одной из наиболее распространенных задач при проектировании зданий и сооружений на топографических планах является определение крутизны склона, т. е. определение уклона или угла наклона по заданному направлению. Эти характеристики можно измерить или графически (по графикам заложений) или по формулам 14 или 15. Для определения крутизны ската графически необходимо иметь графики заложений.

Задача 6.1 .Построить графики заложений для значений ν° и ί, приведенных в таблице 12.

Графики заложений показывают зависимость между крутизной ската и величиной заложения при данной высоте сечения. Так как крутизна ската может быть выражена в градусной мере или процентах, то в соответствии с этими имеется два вида графиков, - для углов наклона и уклонов. Пользоваться такими графиками можно только в случае определения крутизны ската между соседними горизонталями.

Если крутизна ската выражена в градусной мере, то величину заложения a вычисляют по формуле:

a = h0 \ tgν , (19)

а для крутизны ската, выраженной в процентах:

a = h0100/i (20)

где h0 - высота сечения рельефа на карте, выданной для выполнения работы .

Для построения графиков необходимо вычислить заложения a при ν° и i,

приведенные в таблице 13.
Таблица 13.Исходные данные для построения графиков заложений

Углы наклона	0,5°	1°	2°	3°	4°	5°	7°	10°	20°
Заложения а(м)
Уклоны %	1	2	3	4	5	6	8	10	30
Заложения а(м)

При построении графиков на горизонтальной линии откладывают равные отрезки произвольной длины, в концах которых восстанавливают перпендикуляры, и откладывают на них в масштабе своей карты соответствующее значение из табл.13. Концы перпендикуляров соединяют плавной линией.


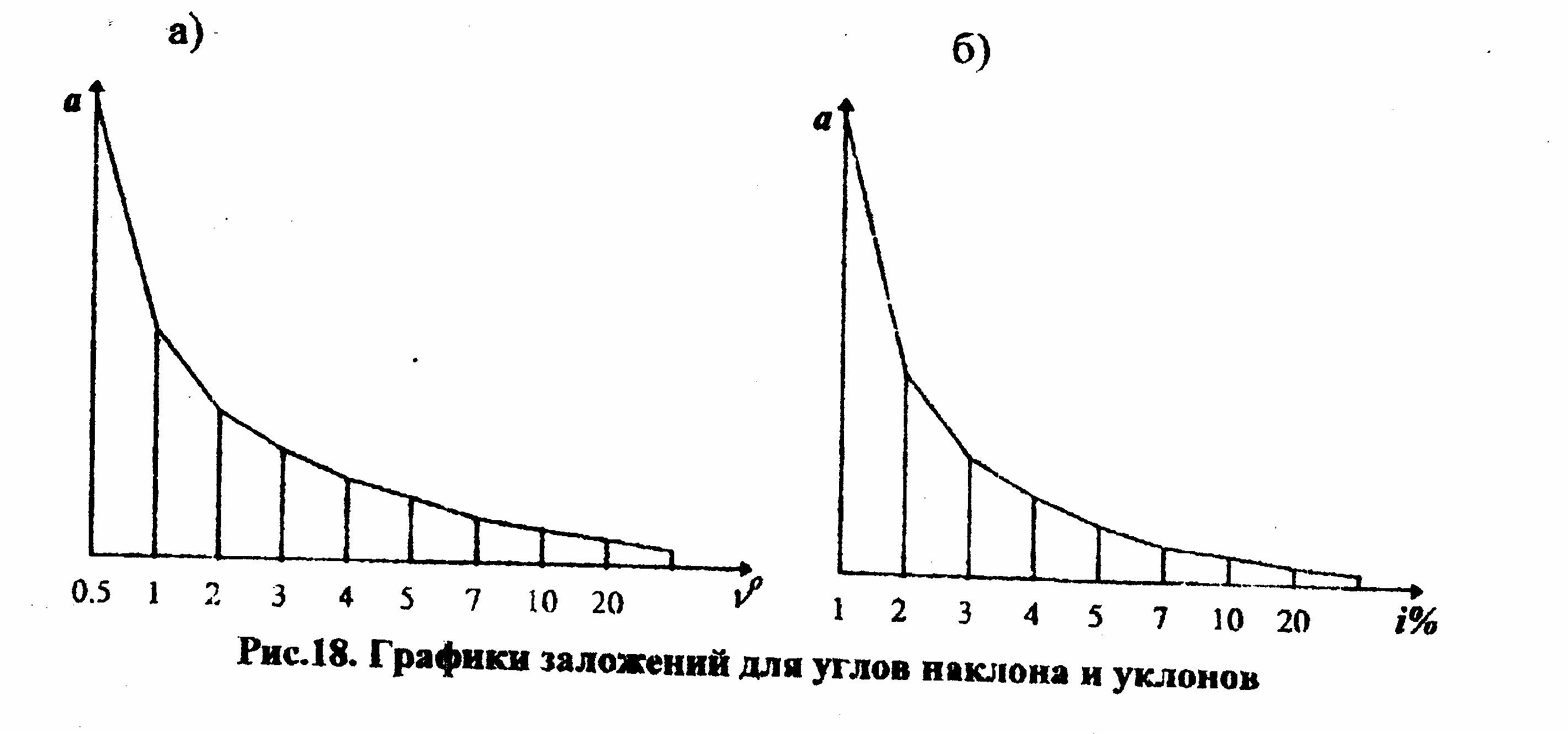
Рис. 19.Графики заложений для уклонов и углов наклона
Задача 6.2. Определить крутизну ската по линии ВС, пользуясь построенными в предыдущей задаче графиками заложений.

Принцип измерения показан на рис.20. Результаты измерения записать в табл.13




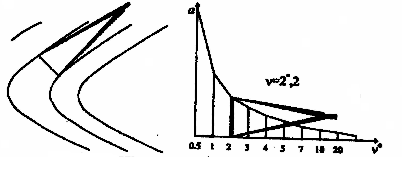
Рис 20.Определение угла наклона по графику заложений
Таблица 13. Крутизна ската по линии АВ

Н0 м		152,5		150,0		150,0		152,5		152,5		150,0		150,0		152,5		155,0
Угол наклона, ν°			2.5		0.0		2.0		0.0		0.9		0.0		1.9		1.2		1.5
Уклон, i %			4.4		0.0		3.4		0.0		1.5		0.0		3.3		2.1		2.6

Еще раз подчеркнем, что характеристики крутизны ската по графикам определяют только между сплошными горизонталями.
Задача 6.3. Построить продольный профиль и вычислить уклон линии на карте, заданной преподавателем.

Линия АВ, по которой должен быть построен профиль, т.е. вертикальный разрез местности по заданной линии, называется профильной, а линия, соединяющая точки А и В – воздушной линией. Данная задача встречается при камеральном трассировании линейных сооружений, например дорог.

Построение профиля осуществляется следующим образом. На миллиметровой бумаге проводят прямую линию, являющуюся основанием профиля, а на нее переносят с карты точки пересечения профильной линии с горизонталями, водоразделами, тальвегами, седловинами и вершинами, выписывая в соответствующую графу (рис.22) их отметки. В полученных точках восстанавливают перпендикуляры и откладывают на них высоты в вертикальном масштабе, который принимают в 10 раз крупнее горизонтального. Для того чтобы чертеж был компактный, все отметки уменьшают на одинаковое число метров, которое называется условным горизонтом (на чертеже 110 м). Его выбирают таким образом, чтобы точка профиля с наименьшей отметкой располагалась на 2-3 см выше основания профиля.



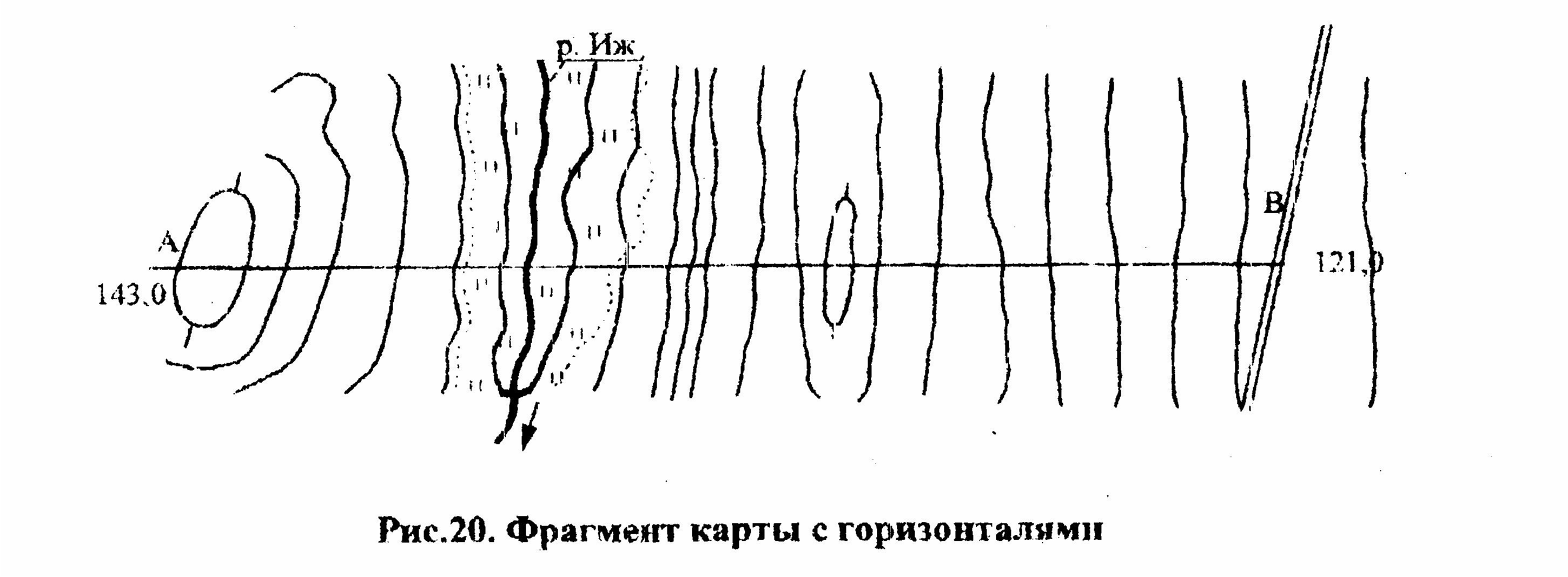
Рис 21. Фрагмент карты с горизонталями
Соединив концы перпендикуляров, получают профиль. Уклон воздушной линии можно получить по формуле:

iAB=(HB-HA)/dAB (21)

где dAB- горизонтальное продолжение линии АВ, выраженное в метрах.

В графу «план трассы» переносят с карты ситуацию, имеющуюся в обе стороны от оси трассы на расстоянии 1 см. Линии, соединяющие точки А и В как на плане так и на профиле, а также в графе уклонов, проводят красным цветом. Ситуацию вычерчивают цветом, соответствующим ее изображению на карте. В графу отметки выписывают высоты точек, повернув подписи на 90 градусов.



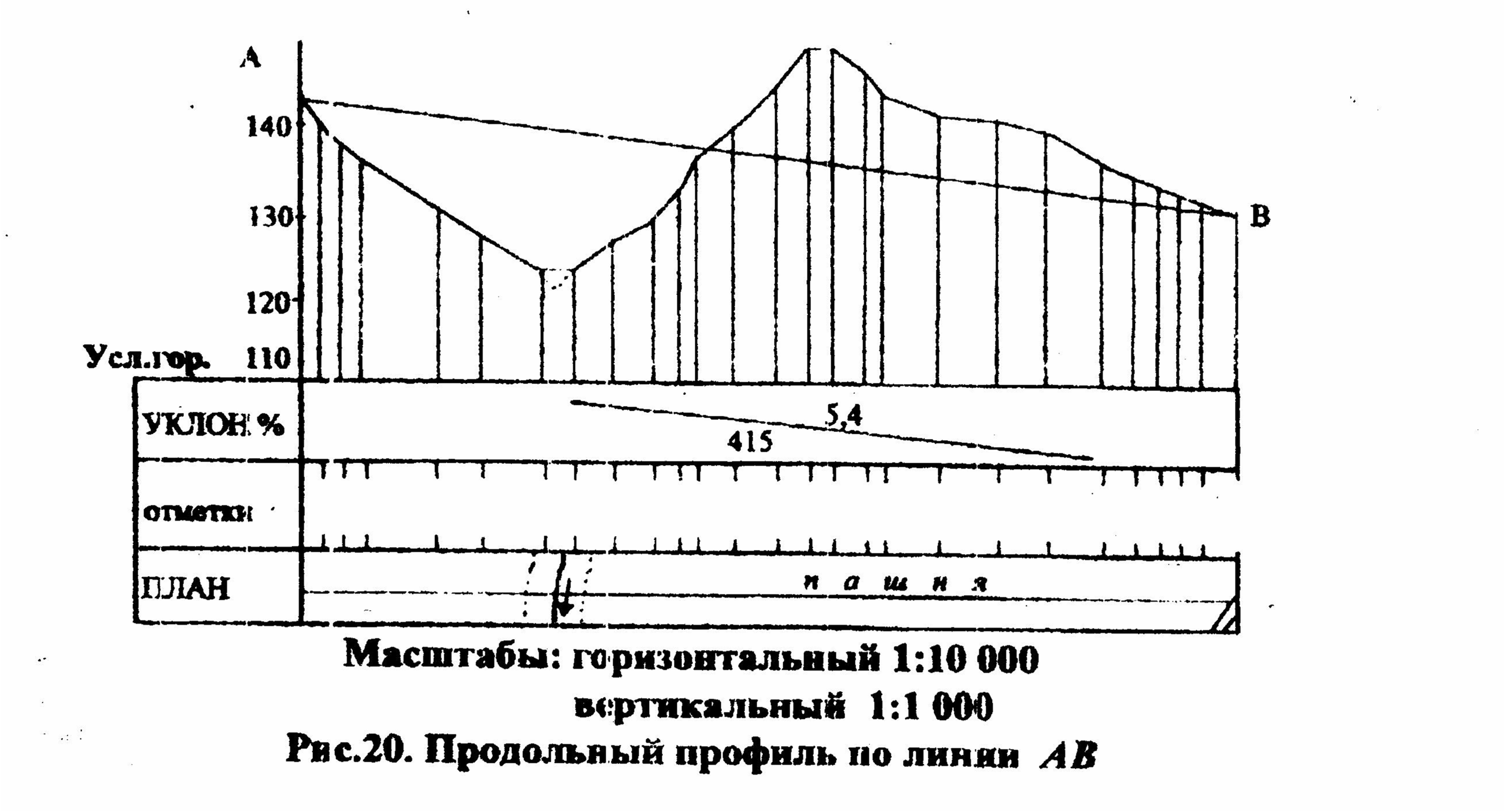
Масштабы: горизонтальный 1:10000

вертикальный 1:1000

Рис 22. Продольный профиль по линии АВ

Примечание. На рис.22 не подписаны высоты горизонталей. На Вашем чертеже они обязательно должны бать подписаны
Задача 6.4. Провести на карте между точками А и С линию с предельным (i_пред) уклоном, заданным преподавателем.
Данная задача встречается при проектировании сооружений линейного типа, когда на строительство такого рода сооружений накладывается ограничение в крутизне ската. Сущность решения такой задачи заключается в проведении из точки А в точку С ломаной линии, ни на одном отрезке которой расстояние между горизонталями не должно быть меньше заложения а, соответствующего предельному уклону. В точках поворота проводимой линии следует избегать острых углов, а длина трассы должна быть минимальной.

Заложение, соответствующее imax определяют с помощью графика заложений для уклонов ( рис.20). Величину a устанавливают на измерителе. Ставят одну иглу в точку А, а второй делают засечку на соседней горизонтали 1. Если вторая игла измерителя не будет доставать горизонтали 1, то проводят линию по направлению АВ. От полученной точки на горизонтали 1 откладывают а в направлении горизонтали 2 и т.д. до точки В. В результате решения задачи может быть несколько вариантов. Предпочтение отдается тому, при котором общая длина линии АВ наименьшая. Пример проведения линии с заданным уклоном приведен в приложении 1.

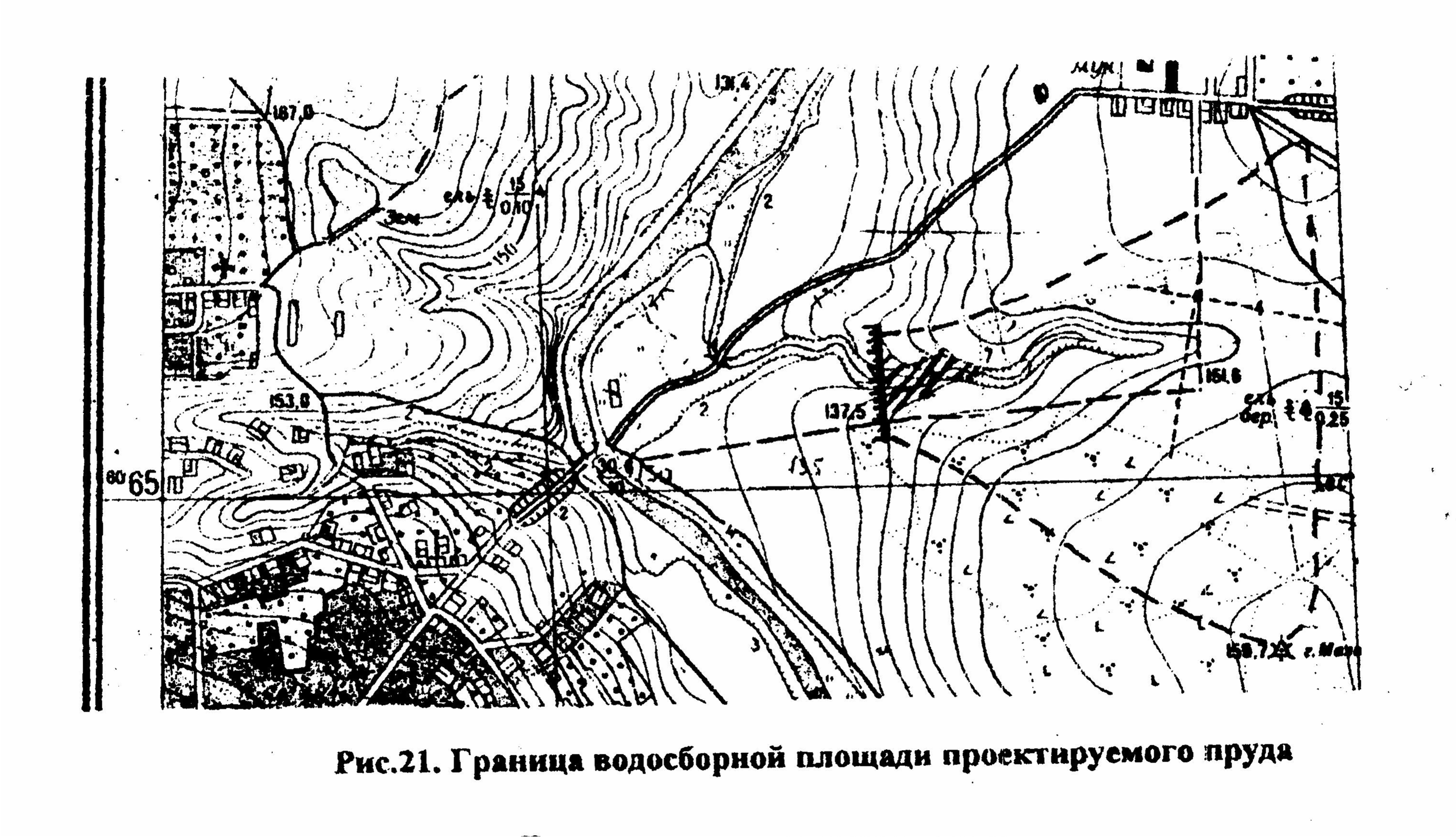
Задача 6.5. Провести границу водосборной площади (бассейна) водоема.
Данная задача встречается при проектировании искусственных водоемов, водопропускных отверстий (труб, мостов) на дорогах и т.д.

Граница водосборной площади проходит по водораздельным линиям хребтов, через вершины гор и перевалы седловин. Проводить границу следует, начиная от плотины в обе стороны, нормально к горизонталям, до встречи с водораздельной линией, а затем уже проводить непосредственно водораздельную линию. Пример проведения водораздельной линии приведен на рис. 23.